卧式液氢贮罐内温度分层数值模拟

王天祥，陈 虹，雷 刚，李爱华

(总装备部工程设计研究总院，北京100028)

1 引言

随着我国航天技术的发展，地面低温推进剂的贮存量越来越大，低温真空绝热贮罐容积也相应增大。在低温推进剂大容量贮存过程中，由于贮罐的绝热性能较高，进入贮罐内部的热量较少，不能完全加热贮罐内的低温推进剂，使得在内部近壁面区域的流体温度升高，在浮升力的作用下沿壁面向上运动，而内部核心流体的温度基本不变，从而在贮罐高度方向形成温度梯度，即温度分层现象.研究表明，温度分层现象不但会导致贮罐内推进剂的上面层形成一定厚度的热液层，影响推进剂的输出品质，而且会恶化容器(贮罐)的使用性能，形成急剧的气枕压力上升［1］。

国内外对低温容器内温度分层的研究进年来也有相关报道。文献［2］采用涡流函数法对低温流体液氢热分层进行了数值模拟，同时拟合出表面温度对热流密度、液体填充率及时间的函数表达式。文献［3］利用边界层积分方法对火箭液氢推进剂的热分层进行了分析，并选用水作为研究工质进行了模拟实验。文献［4］采用试验方法对大型容器内液氢热分层现象进行了研究，并分析了振荡与晃动对液氢热分层现象的影响。文献［5］通过对方型透明容器采用壁面加热的可视化试验方法，进行了水的热分层现象实验研究，并且采用数值模拟的方法对圆柱型筒体内液氢的热分层规律进行了分析，两种结果对比得到了相似的结论。文献［6］等针对两个典型的液化天然气涡旋事故，分析了分层和涡旋现象的机理，并且对双向对流扩散模型、Bates-Morrison模型和四阶段模型等进行了介绍。文献［7］分析了液化天然气贮槽内分层现象形成的原因、分层稳定性和破坏性的机理以及分层的存在对各个液体层之间的传热和传质的影响，并给出了此种情况下的热流率和质流率的计算关联式。文献［8］采用大涡模拟方法对港口取水系统进行了数值计算，得到了水温与流速的分布。文献［9，10］用FLUENT对火箭液氧竖直贮箱内液氧温度场和速度场进行了数值模拟，得到了火箭液氧贮箱内温度与速度分布。文献［11］采用CFD技术，对不同气枕压力下液氢贮箱内部物理场进行数值模拟。研究表明:气枕压力会对贮箱内部温度场与速度场产生重要影响。根据现有文献资料，目前大多数研究主要集中在立式圆柱形容器的热分层方面，对大容量卧式贮罐内低温推进剂(尤其是液氢)温度分层的研究很少。同时，低温推进剂卧式贮罐结构庞大，加之液氢/液氧自身的物性特殊，进行可视化等实验研究非常困难。

因此，本文采用CFD技术通过对大型卧式液氢贮罐内温度场的数值模拟，揭示贮罐内部压力场、温度场的分布规律，分析了液氢热液层的形成过程及原因，为发射场大规模低温推进剂的安全贮存和确保输出推进剂品质提供了重要的理论支撑。

2 模型建立与边界条件

液氢贮罐由水平圆柱体及左右两椭圆型封头组成，容积300 m3，采用内外罐结构，内罐光滑，绝热方式为高真空绝热。由于时间跨度长，计算量巨大。由于储氢罐是横向放置，相对于垂直方向，水平方向的传热与流动可以忽略，故可以简化为两维问题。计算中采用二维结构化网格，左右壁面用边界层网格局部加密，计算网格如图1所示。

图1 模型网格

由于液氢贮罐内存在自由相界面，计算中选用VOF模型和二维非稳态粘性流体k－ε模型相结合的计算模型，采用热边界条件、标准壁面函数和基于压力的计算方法。另外，由于液氢的特殊属性，液氢密度采用Boussineqs模型，编写了氢气的密度、比热、导热系数等自定义函数。同时，针对FLUENT软件自带模型在解决相变问题时应用范围狭窄、模型也不够完善的缺点，为了对液氢贮罐内的物理场进行较为准确的模拟，编写了相变模型的自定义程序。

描述贮罐内部流动及传热的控制方程为:

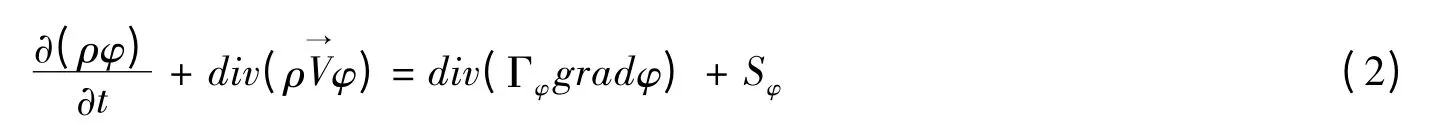
式中 φ为广义标量，可以表示速度u，v，湍流脉动动能k，湍流脉动动能耗散率ε，温度T。αp为气态氢，αq为液态氢。ρ为密度，Γφ、Sφ分别表示扩散项和源项。

由于外部热侵使得贮罐内部会发生气液两相的质量和能量的变化，因此，为了较为真实的模拟贮罐内部的物理现象，本模型通过定义连续性方程(1)中的和和能量方程中的源相来模拟液相蒸发过程，采用赫兹一努森方程，将其编写成程序后外挂于Fluent进行计算。

本研究的初始条件和边界条件为:初始气枕压力为1 atm，气枕温度为20.2 K，液体温度为20 K，液氢填充率0.5;边界为壁面边界条件，输入热量为1.1 w/m2。

3 计算结果及分析

由于贮罐受到外部环境的热侵，导致贮罐内的液氢汽化，从而使得气枕压力升高。对于贮罐内压力的变化可以通过简化理论给出计算值。假定氢气和液氢在各自部分充分混合，温度均匀，则可通过传入贮罐内的热量，推导出能够蒸发出的液氢量，从而根据氢气状态方程，计算出贮罐内压力变化，如图2所示。图2也同时给出了CFD计算的压力随时间变化率。从图中可以看出，随着贮存时间的增加，贮罐内气枕压力逐渐上升，理论计算得到的压力增长速率要小于CFD计算结果，这是由于在理论计算时没有考虑贮罐内液体的温度分层，壁面漏热被认为是均匀的加热整个液体，所以蒸发的液氢量相对于考虑温度分层时要小。因此，在静置贮存时，由于温度分层会导致液氢贮罐内的压力急剧上升。同时，CFD计算结果显示，压力先开始有下降过程，是因为计算时的初始值液氢未达到饱和，故氢气向液氢传热导致氢气温度下降从而有压力降低过程。

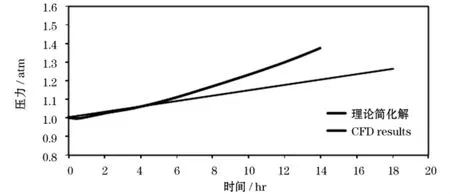
图2 数值模拟与理论计算气枕压力比较

图3 为静置卧式贮罐横截面上的流体流动速度矢量图，从图中可以看出，贮罐内部流动是一个不稳定状态，涡旋的位置也在不断变化。随着贮存时间的增加，液相近壁处的边界层内热液体在浮升力的作用下沿壁面向上运动，积聚于气液界面，而气液界面下的冷流体向下运动，形成了明显的自然对流。由于受贮罐圆形横截面的影响，热液层内液体质点沿弧形轨迹运动时，每一个点的受力情况与竖直贮罐内的情况截然不同，从而导致冷液体在向下运动时不完全是沿重力方向，其流线在不同时间具有不同的形状，部分地方出现了更为复杂的涡旋流动。卧式贮罐内的这种复杂流动，在一定程度上对液体的温度分层起到了抑制作用，减小了容器压力急剧上升的危险性，但对贮罐内液体的输出品质(温度)有一定的不利影响，因此，在液氢加注或输送之前需要首先对贮罐泄压，以保证液氢输出品质。

图4为静置卧式贮罐内流体温度分布图，从图中可以看出，卧式贮罐的边界层覆盖了整个与液体接触的贮罐内壁，由底部向液体表面厚度逐渐增厚。随着贮存时间的增加，贮罐内竖直方向上液体形成了较为明显的温度分层。在贮存过程中，通过贮罐内壁面附近热边界向气液界面不断输送热液体，使得气液界面下的热液层不断增厚，同时，由于贮罐内液体的不稳定流动，使得贮罐内的主体液体的温度也有少许增加。由于气液界面一直处于动态平衡过程，其温度也基本处于气枕压力下的饱和温度，这可以通过图2和图4看出。

图5是静置卧式贮罐横截面竖直方向上温度随时间变化曲线图。随着贮存时间的增加，气液表面的热液层厚度(气液界面温度与主体液体温度之间的区域)逐渐增加，热液层内存在着一定的温度梯度，其分布接近于高斯概率曲线，且气相区也存在着非线性的温度分布。在静置贮存15小时后，热液层的最高温度与主体液体温度相差1 K左右，而气相最高温度出现在顶部，约60 K左右。

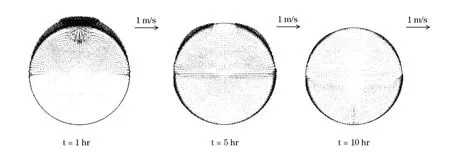
图3 静置卧式贮罐内流体速度矢量图

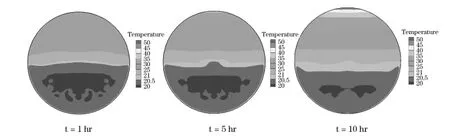
图4 静置卧式贮罐内流体温度分布图

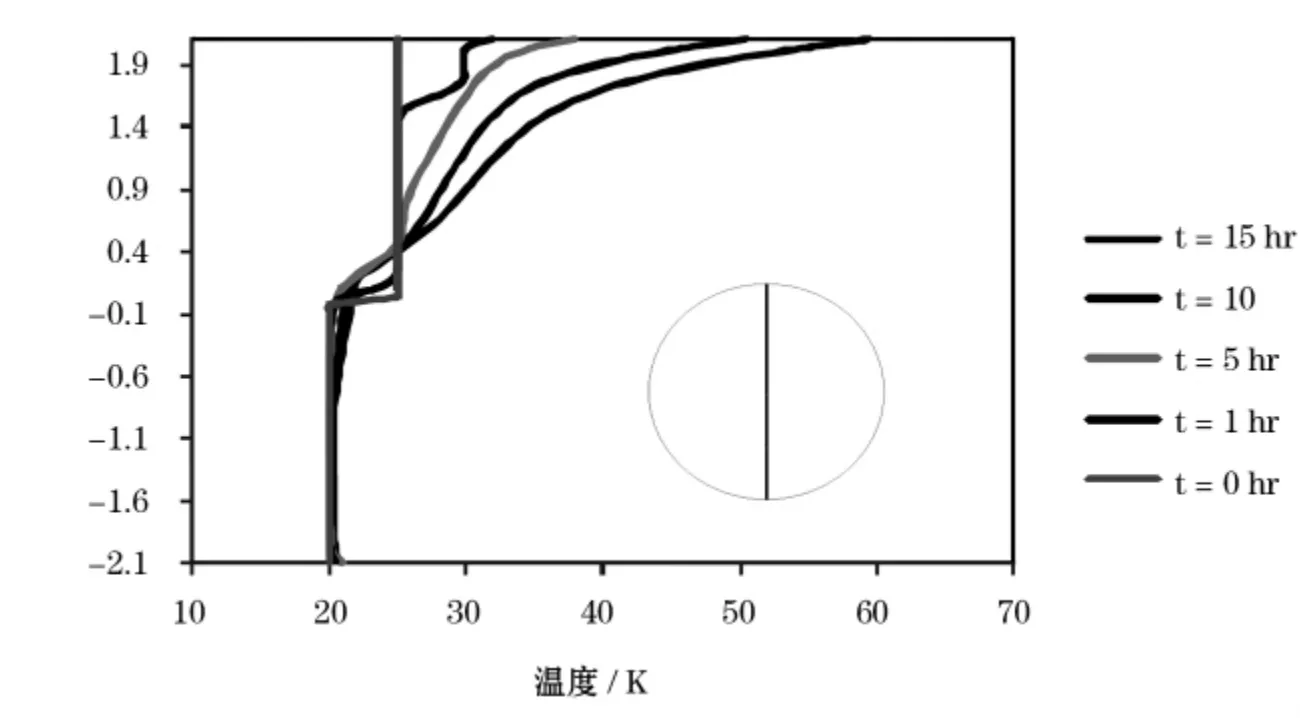
图5 静置卧式贮罐横截面竖直方向上温度分布曲线

4 结论

(1)静置卧式贮罐罐壁与液氢的换热为带边界层的自然对流换热，边界层覆盖整个与液氢接触的贮罐内壁面。

(2)静置卧式贮罐内的液氢沿竖直方向上出现温度分层，其温度分布近似于高斯概率曲线，最高温度为气液界面处的气枕压力下的饱和温度，最低温度为主体液氢的温度。气相区域存在着非线性的温度分布，最高温度出现在贮罐顶部。

(3)静置贮罐内的液氢处于不稳定流动状态，在局部地方有涡旋流动。卧式贮罐内的这种复杂流动，使得贮罐内的主体液体的温度也有少许增加，在一定程度上对液体的温度分层起到了抑制作用，减小了容器压力急剧上升的危险性，但对贮罐内液体的输出品质(温度)有一定的不利影响，因此，在液氢加注或输送之前需要首先对贮罐泄压，以保证液氢输出品质。

［1］尼瓦费林，亚波布拉诺夫.液体低温系统［M］.北京:低温工程编辑部，1993.

［2］Tanyun Z，Zhongp in H，Li S.Numerical simulation of thermal stratification in liquid hydrogen［J］.Advances in Cryogenic Engineering，1996，41:155 ～161.

［3］Tatom JW，BrowW H，KnightL H，et al.Analysis of thermal stratification of LH2 in rocket propellant tank［J］.Advances in Cryogenic Engineering，1964，9:265 ～272.

［4］Bailey T E，Fearm R F.Analytical and experimental determination of LH2 temperature stratification［J］.Advances in Cryogenic Engineering，1964，9:254～264.

［5］DAS S P，CHAKRABORTY，DUTTA P.Studies on thermal stratification phenomenon in LH2 storage vessel［J］.Heat transfer engineering，2004，25(4):54～66.

［6］林文胜，顾安忠，李品友.液化天然气的分层与漩涡研究进展［J］.真空与低温，2000，6(3):125～132.

［7］程 栋，顾安忠.液化天然气的贮存分层现象［J］.深冷技术，1997(1):13～15.

［8］江春波，马强，付清潭.二维温度分层流的数值模拟［J］.水力发电，2003(2):24～26.

［9］程向华，厉彦忠，陈二峰.火箭液氧贮箱热分层现象数值模拟［J］.低温工程，2008(2):10～13.

［10］程向华，厉彦忠，陈二峰，等.新型运载火箭射前预冷液氧贮箱热分层的数值研究［J］.西安交通大学学报，2008(9):1132～1136.

［11］王磊，厉彦忠，程向华.气枕压力对液氢贮箱热分层的影响规律［J］.低温工程，2009(6):18～22.