倾向得分区间匹配法用于非随机对照试验的探索与研究*

张 亮 李婵娟△ 夏结来△ 王永吉 王 陵 蒋志伟

在临床试验、流行病学病因研究以及大部分观察性试验研究和设计中，倾向得分方法已经被广泛的应用到这些非随机对照试验中来降低由于混杂因素导致的选择性偏倚，从而保证组间基线数据的均衡可比〔1－3〕。倾向得分是在给定可观察的基线协变量条件下，研究对象分配到处理组或者对照组的条件概率，如果处理分配是强可忽略(strongly ignorable)的，那么根据倾向得分可获得平均处理效应的非偏估计〔4〕。倾向得分方法包括:匹配(matching)、分层(stratification)、回归校正(regression adjustment)、加权(weighting)等。其中匹配法在观察性数据研究中应用最为广泛。本文通过Monte Carlo模拟产生数据集，利用倾向得分的95%置信区间进行匹配，并与logistic回归分析和倾向得分卡钳匹配比较，探索研究倾向得分区间匹配法在均衡组间协变量降低选择性偏倚从而正确估计处理效应的能力。

倾向得分介绍

1.定义

早在1976年，Miettinen就提出用多元混杂因子把多个协变量综合成为一个单一变量〔5〕。1983年，Rosenbaum和Rubin提出了在队列研究中，基线期估计倾向得分(propensity scores，PS)控制选择性偏倚〔4〕。在流行病学研究中，估计药物处理效应和试验处理的结果时用这种方法控制因混杂因素导致的选择性偏倚越来越流行。根据研究对象的所有观察特征，通常采用一个多变量logistic回归模型来估计倾向得分。倾向得分的范围在0到1之间，它表示研究个体分配到处理组或对照组的概率。具有相同倾向得分的研究对象有着相同的机会接受处理，任何具有相同倾向得分的两个研究对象，对于具体的协变量可能值不相同，但是对于进入模型的全部协变量将在组间趋于均衡〔6〕。假定在所有协变量都被观察到的情况下，采用PS法，就好像进行了随机分配一样，所以有的研究者称之为“事后随机化”。

倾向得分的定义:在观察到的协变量(xi)条件下，研究对象i(i=1，…，N)被分配到特定处理组(Zi=1)而非对照组(Zi=0)的条件概率，可以表达为:

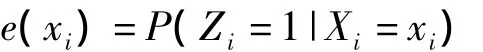
假定在给定的一组特征变量Xi下，分组变量是独立的，则:

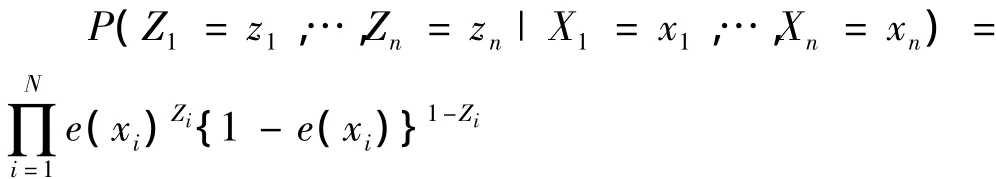
倾向得分是组间均衡性的一个函数，反应观察到的所有协变量体现个体特征的作用，从而可以有效控制混杂因素使得组间各个协变量均衡一致。

2.估计方法

倾向得分估计的方法有很多种，目的是把影响处理因素的众多协变量用一个单值的倾向得分来表示，然后再进行分析。倾向得分的估计方法有:①广义线性模型(包括logistic回归模型、Probit模型、广义加法模型等);②判别分析;③Cox风险模型;④分类树技术;⑤神经网络技术;⑥贝叶斯估计等。其中logistic回归模型是最常用也是最简便易行的方法。

logistic回归属于概率型非线性回归，其模型的参数具有鲜明的实际意义，现已成为处理二分类反应数据的常用方法〔7〕。

3.PS匹配法

倾向得分匹配是在所有进入对照组的个体中选择与进入处理组个体倾向得分相同或相近的个体与之配对，从而达到均衡组间协变量的目的。在所有协变量都可以被观察到的情况下，通过倾向得分匹配可以得到处理效应的无偏估计〔8〕。

卡钳匹配(caliper matching)的定义是处理组与对照组个体倾向得分差值在事先设定的某个范围内才能进行匹配。卡钳的设定是非常重要的，Austin多次通过Monte Carlo模拟比较了研究者实际应用中经常选用的卡钳值，研究结果证明最合适的卡钳值是倾向得分经logit变换后标准差的20%或者将其绝对值设为0.02、0.03〔9〕。

区间匹配(interval matching)利用的是每个个体的倾向得分95%置信区间进行匹配，方法是从处理组第一个个体开始，在对照组中找到置信区间与之重合最多并且重合需大于处理组个体置信区间的特定百分比，满足这个条件的个体作为匹配对象，然后对照组中匹配了的个体不参与处理组其他个体的匹配即进行无放回匹配(图1)。

图1 倾向得分匹配法与倾向得分区间匹配法

4.PS评价指标

本文用检验效能、I类错误、标准化差异以及匹配比例四个指标来评价比较倾向得分区间匹配法和logistic回归分析以及倾向得分卡钳匹配，其中标准化差异能够很好地反映组间协变量的均衡情况。

标准化差异在近年的倾向得分研究中应用较多〔10〕，其概念由Flury和Reidwyl在1986年首次提出〔11〕。

对于二分类变量，标准化差异定义为:

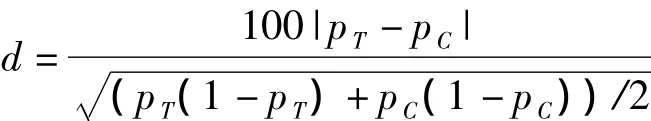
其中，pT和pC分别表示处理组和非处理组中待检验变量的阳性率。

对于连续性变量，标准化差异定义为:

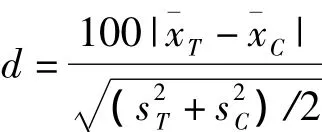
计算机模拟

采用Monte Carlo模拟比较倾向得分区间匹配法、倾向得分卡钳匹配法和logistic回归分析三种方法，数据模拟和统计分析通过软件SAS 9.1实现。本研究经过两次建模，多次模拟来评价倾向得分区间匹配法均衡组间协变量的能力。

1.模拟方法

根据协变量与处理因素和结局变量的关系，协变量可分为:①只和处理因素有关;②只和结局变量有关;③与处理因素和结局变量都有关;④与处理因素和结局变量都无关。根据这四类变量和相关程度强弱，本文模拟的协变量包括表1所列9个协变量。

表1 模拟协变量的分类

Monte Carlo模拟的目标就是检验倾向得分区间匹配法在处理组间均衡这9个协变量的能力〔13〕。根据Bernoulli分布产生9个独立的随机二分类协变量，利用 SAS 9.1的函数 rand('bernoulli'，P)，P=0.5产生数据集。然后对每个研究对象采用Bernoulli分布根据下列回归模型生成一个分组变量Ti:

其中，β0，treat为常数项，调节 β0，treat可以控制处理组与对照组间样本比例，β1～β6为回归系数，exp(βi)为与处理因素有关的各协变量OR值。

再对每一个研究对象，在分组变量Ti的条件下，根据下列回归模型及Bernoulli分布产生一个结果变量Yi:

其中，α0，outcome为常数项，调节 α0，outcome可以控制对照组阳性结果的发生率，βtreat、α1～α6为回归系数，exp(βtreat)为处理因素的OR值，exp(αi)为与结果有关的各协变量OR值。

2.模拟设置

(1)弱相关模型:

对于上面两个logistic回归中协变量的回归系数，设定弱相关模型参数为:中等相关的回归系数为log(1.25)，强相关的回归系数为 log(1.5)。设定 β0，treat=－1.366，这样就能保证大约40%的研究对象进入到处理组。设定α0，outcome=－2.688，保证对照组阳性结果的发生率约为15%。βtreat的设定:log(1.1)、log(1.5)、log(2)、log(2.5)和 log(3)。通过改变 β0，treat、α0，outcome和βtreat这三个参数，可以调整处理组与对照组的比例，对照组阳性结果的发生率，和处理因素与结果效应的关系。模拟产生1000个样本量为500的数据集进行倾向得分区间匹配研究分析并与卡钳值为倾向得分经logit变换后标准差的20%的卡钳匹配以及传统的logistic回归分析进行比较〔14〕。

(2)强相关模型:

调整模型参数，对于上面两个logistic回归中协变量的回归系数，设定强相关模型参数为:中等相关的回归系数为log(1.5)，强相关的回归系数为log(1.75)。设定β0，treat=－1.889，这样就能保证大约40%的研究对象进入到处理组。设定α0，outcome=－3.687，保证对照组阳性结果的发生率约为10%。模拟产生1000个样本量为500的数据集进行倾向得分区间匹配研究分析并与卡钳值为倾向得分经logit变换后标准差的20%的卡钳匹配以及传统的logistic回归分析进行比较。

3.模拟结果

(1)最优卡钳区间的选择

我们分别设定卡钳区间为处理组个体倾向得分置信区间长度的90%、85%、80%、70%进行模拟匹配，通过检验效能、I类错误、标准化差异、匹配比例四个指标来评价，然后得出最优卡钳区间值。

表2 两种模型下不同卡钳区间匹配评价

通过模拟不同卡钳区间进行匹配，我们可以从表1中看出，当卡钳区间选择处理组置信区间的80%时，检验效能、I类错误、标准化差异和匹配比例都是令人满意的。根据卡钳区间为80%，进一步模拟比较区间匹配法、logistic回归法和卡钳匹配法的检验效能、I类错误、标准化差异和匹配比例。

(2)检验效能

区间匹配、logistic回归及卡钳匹配三种方法在强弱相关两种模型下的检验效能比较结果见表3。

当处理因素OR值不断增大时，三种方法在两种模型下的检验效能都是逐渐增大的。不管是强相关模型还是弱相关模型，logistic回归法的检验效能均高于区间匹配法，区间匹配法均高于卡钳匹配。进一步模拟表明，改变处理组与对照组的比例，改变对照组阳性结果发生率，其结论不变。

(3)I类错误

区间匹配、logistic回归及卡钳匹配三种方法在强弱相关两种模型下的Ⅰ类错误比较结果见表4。

表3 三种方法两种模型在不同处理因素OR值下的检验效能(%)

在弱相关模型和强相关模型中，logistic回归法的I类错误最低，但三种方法都能控制I类错误在0.05以内。在强相关模型中，区间匹配法的I类错误和卡钳匹配基本一致，logistic回归法的I类错误高于其他两种方法，三种方法都能将I类错误控制在0.05左右。进一步模拟表明，改变处理组与对照组的比例，改变对照组阳性结果发生率，其结论不变。

(4)标准化差异

PS区间匹配法和PS卡钳匹配法在强弱相关两种模型下的标准化差异比较结果见表5。

表4 三种方法两种模型的I类错误

表5 不同方法两种模型的标准化差异(%)

在弱相关模型下，区间匹配法和卡钳匹配法都能很好的均衡各个协变量，其与结果有关的协变量的标准化差异均小于10%，而在强相关模型下，区间匹配法能够将全部的9个协变量的标准化差异全部降低到10%以内，均衡了所有的协变量。

(5)匹配比例

PS区间匹配和PS卡钳匹配两种方法两种模型的匹配比例比较结果见表6。

表6 不同方法两种模型的匹配比例(%)

在弱相关模型下，区间匹配的匹配比例高于卡钳匹配，也是其检验效能高于卡钳匹配的一个原因;在强相关模型下，两者的匹配比例要低于弱相关下的匹配比例，区间匹配在强相关模型下处理组个体的置信区间变窄，导致匹配精度的提高;强相关模型下，区间匹配的匹配比例略低于卡钳匹配，但是其检验效能在不同处理因素OR值下是高于卡钳匹配的。

讨 论

通过上面的模拟研究发现:(1)采用倾向得分区间匹配法能够很好的均衡组间协变量。(2)从检验效能、I类错误、标准化差异和匹配比例四个评价指标等综合考虑认为卡钳区间设为处理组置信区间的80%是合适的。(3)通过模拟比较，区间匹配法在四个评价指标中与logistic回归法和倾向得分卡钳匹配无明显差异，区间匹配法在处理因素不同OR值的情况下的检验效能稍好于卡钳匹配，其I类错误也小于卡钳匹配。用标准化差异判断两种方法均衡协变量的能力时，区间匹配法和卡钳匹配都能均衡组间协变量。(4)两种模型下，区间匹配法、logistic回归法和卡钳匹配都有良好的检验效能和控制I类错误的能力。不管是弱相关模型还是强相关模型，logistic回归法稍好于区间匹配法，区间匹配法稍好于卡钳匹配法。区间匹配法在强相关模型下均衡组间协变量的能力比弱相关模型更强。倾向得分区间匹配法在观察性研究中均衡组间协变量的能力得到了印证，也反映出倾向得分区间匹配法的可行性和实用性。

在流行病学病因研究、大量的观察性研究中，运用倾向得分区间匹配法能够有效地均衡组间协变量的分布，在组间协变量均衡的基础上进一步评价处理因素的效应，从而得到接近随机对照研究的结果〔15〕。由于倾向得分是协变量的一个函数，无论有多少个协变量，都可以综合成为一个倾向得分来表示，实际上起到了降维的作用，而且倾向得分区间匹配法操作简便，容易理解，能够很好地对结果进行解释。logistic回归法用于分析结局变量与协变量之间的关联关系，而倾向得分方法推断的是因果关系，在因果关系论证强度上大于logistic回归法。倾向得分方法同样适用于混杂因素很多，结局变量发生率很低的情况，而logistic回归法并不适合〔16〕。另外，某些非随机化临床试验，如医疗器械的临床评价，Ⅳ期临床试验等，可以通过倾向得分方法进行分析〔17〕。

倾向得分方法在实际应用中，研究者一定要对数据资料和方法有足够的了解，因为倾向得分方法永远只是局限于可观察到的协变量，而一些未知的混杂因子仍然可能对结果产生影响。因此科学运用倾向得分方法可以有效地控制混杂因素，得到结果的无偏估计。

本研究的局限性在于:(1)只模拟了二分类协变量的情况，没有对多分类和连续型协变量进行模拟;(2)模型只选择了弱相关模型和强相关模型两种进行研究分析;(3)只选择了四类评价指标进行综合评价;(4)对于最优卡钳区间的选择上只局限于简单的模拟。对于本研究的不足，我们将在以后进一步分析研究。

1．Austin PC．A critical appraisal of propensity-score matching in the medical literature between 1996 and 2003．Statistics in Medicine，2008，27:2037-2049．

2．Austin PC．Type I Error Rates，Coverage of Confidence Intervals，and Variance Estimation in Propensity-Score Matched Analyses．The international Journal of Biostatistics，2009，5:1-21．

3．Newgard CD，Hedges JR，Mullins RJ．Advanced Statistics:The Propensity Score—A Method for Estimating Treatment Effect in Observational Research．Academic Emergency Medicine，2004，11:953-961．

4．Rosenbaum PR，Rubin DB．The central role of the propensity score in observational studies for causal effects．Biometrika，1983，70:41-55．

5．Miettinen OS．Stratification by a multivariate confounder score．Am J Epidemiol，1976，20:104-609．

6．Til Stürmer，Manisha Joshi，Glynn RJ，et al．A review of the application of propensity score methods yielded increasing use，advantages in specific settings，but not substantially different estimates compared with conventional multivariable methods．Journal of Clinical Epidemiology，2006，59:437-447．

7．孙振球，徐勇勇主编．医学统计学．第2版．北京:人民卫生出版社，2008，333-336．

8．Austin PC，Mamdani1 MM．A comparison of propensity score methods:A case-study estimating the effectiveness of post-AMI statin use．Statistics in Medicine，2006，25:2084-2106．

9．Austin PC．Some methods of propensity-score matching had superior performance to others:results of an empirical investigation and Monte Carlo simulations．Biometrical Journal，2009，51:171-184．

10．Perkins SM，Tu W，Underhill MG，et al．The use of propensity scores in pharmacoepidemiologic research．Pharmacoepidemilology and Drug Safety，2000，9:93-101．

11．Flury BK，Reidwyl H．Standard distance in univariate and multivariate analysis．The American Statistician，1986，40:249-251．

12．Normand SLT，Landrum MB，Guadagnoli E，et al．Validating recommendations for coronary angiography following an acute myocardial infarction in the elderly:a matched analysis using propensity scores．Journal of Clinical Epidemiology，2001，54:387-398．

13．Austin PC．Comparing paired vs non-paired statistical methods of analyses when making inferences about absolute risk reductions in propensity-score matched samples．Statistics in Medicine，2011，30:1292-301．

14．Dehejia RH，Wahba S．Propensity score-matching methods for nonexperimental causal studies．Review of Economics and Statistics，2002，84:151-161．

15．詹思延主编．流行病学进展．第12卷．北京:人民卫生出版社，2010，358-375．

16．王永吉，夏结来，蔡宏伟，等．倾向指数匹配法与logistic回归分析方法对比研究．现代预防医学，2011，38(12):2017-2018．

17．王永吉，蔡宏伟，夏结来，等．倾向指数(第一讲):倾向指数的基本概念和研究步骤．中华流行病学杂志，2009，31(3):347-348．