季节时间序列模型在菌痢发病预测中的应用
胡建利 梁 祁 吴 莹 刘文东 艾 静 李 媛 张永杰 彭志行 鲍昌俊
传染病的发病受到很多因素影响,而且影响因素之间又存在错综复杂的关系,因此静态的因果结构模型很难揭示其流行趋势,而根据事物自身变动规律建立动态模型——时间序列进行预测分析则是一种行之有效的方法。自回归移动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)是一类常用的随机时间序列模型,已广泛地应用于金融保险、社会科学、自然科学等领域中〔1,2〕,能比较准确地对序列未来各期进行预测。
肠道、呼吸道和自然疫源性传染病的发病由于受到季节性因素或其他一些固有因素的影响,存在明显的周期性变化。描述这类资料需要使用季节时间序列模型(Seasonal ARIMA Model,SARIMA)。本文运用SARIMA模型对江苏省菌痢的月发病数建立数学模型,定量地预测其发病情况,并探讨该模型进行传染病预警的可行性。
资料和方法
1.资料来源
1990~2003年的菌痢统计数据来源于江苏省法定传染病年报表,2004~2010年的菌痢统计数据来源于江苏省疾病监测信息报告管理系统。
2.方法与原理
(1)基本思想
SARIMA模型:较早的文献也称其为乘积ARIMA模型,是随机季节模型与ARIMA模型的结合,对于时间序列{Zt,t=1,2,…}有季节性、趋势性和周期性时,可以建立非平稳季节模型,表示为SARIMA(p,d,q)(P,D,Q)模型。其一般形式为〔3〕:
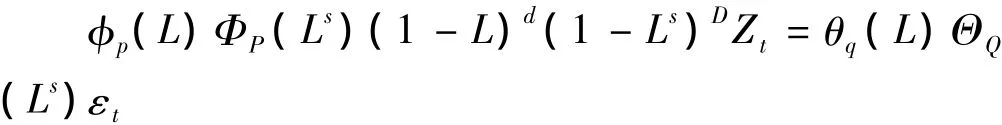
其中:φp(L)=1-φ1L-φ2L2-… -φpLp,p为非季节自回归阶数。
ΦP(Ls)=1-ΦsLs-Φ2sL2s-… -ΦPsLps,P为季节自回归阶数。
θq(L)=1-θ1L-θ2L2-… -θqLq,q为非季节移动平均阶数。
ΘQ(Ls)=1-ΘsLs-Θ2sL2s-… -ΘQsLQs,Q 为季节自回归阶数。
d,D分别为普通差分和季节差分的阶数,s为季节的长度。εt为白噪声序列。
(2)建模过程
①数据的平稳化
在确定时间序列模型之前需把不平稳的时间序列转化为平稳的序列。通常将原序列进行自然对数变换消除其异方差,然后根据变换后序列的自相关和偏自相关图,确定非季节差分阶数d和季节差分阶数D,d和D宜取较低阶(通常取1,2,3),s可以根据疾病的背景知识获得。
②模型参数的估计
根据变换后的平稳时间序列进行分析,尤其是序列的自相关和偏自相关图,估计模型p、P、q、Q的值,采用最大似然估计或最小二乘法估计等对初步估计的模型进行检验。如果检验不通过,则调整参数,重新估计并检验,直至检验通过为止。
估计的模型通过检验是指:模型的参数必须通过t检验,且全部特征根的倒数都小于1〔4〕。
③模型的诊断检验
模型参数估计后,应该对模型的残差是否为白噪声进行检验,若残差序列不是白噪声序列,意味着残差序列还存在有信息没被提取,需要进一步改进模型。
实际运用中,可以获得多个时序模型,为了得到一种最佳模型,可借助拟合优度统计量来对比各个模型的优劣。其中最常用的是调整后的决定系数、AIC和SC统计量。
3.数据分析
采用Eviews 5.0软件进行数据的处理和分析。1990年1月~2009年12月菌痢月发病数数据用于建立模型,2010年1~5月数据用于验证模型的预测效果。
结 果
1.资料分析
江苏省1999年1月至2009年12月菌痢逐月发病数(Zt)曲线呈明显的非平稳性和季节性,并伴随一定的周期性波动,见图1。菌痢属于肠道传染病,发病有明显的高峰季节:每年7~8月份发病率最高,12月至次年2月发病率最低。

图1 原始数据Zt序列图
2.建立数学模型
(1)数据的平稳化
从图1可以看出,原始数据序列随着时间呈现递减型异方差。因此对原始数据首先进行自然对数转换,以平稳序列的方差。对数变换后的菌痢月发病数据(LnZt)自相关图和偏自相关图,见图2。从图2中可以看出自相关图衰减很慢,说明LnZt是非平稳的,且相关图存在周期为12个月的季节波动。因此对LnZt进行一阶非季节差分和一阶季节差分,得到ΔΔ12LnZt。从序列ΔΔ12LnZt的相关图和偏相关图(图3)可以看出,其自相关函数快速衰减,近似为一个平稳过程。
(2)模型参数的估计
由于原始序列Zt对数变换后,经过一阶非季节性差分和一阶季节性差分达到平稳,因此d=1、D=1。观察序列ΔΔ12LnZt的偏相关图,序列ΔΔ12LnZt的偏相关函数在滞后2阶、12阶、24阶显著地不为零(超过其95%的置信区间),因此p=2(尽量选取低阶);序列ΔΔ12LnZt的自相关函数在滞后2阶、12阶显著地不为零,因此q=2;由于相关图和偏自相关图在滞后12阶都显著不为零,因此P=1、Q=1。
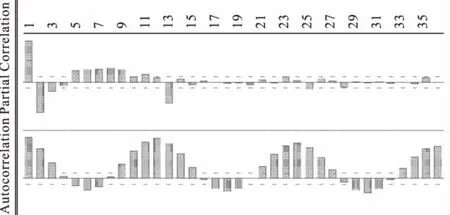
图2 序列LnZt的相关图(下)和偏相关图(上)
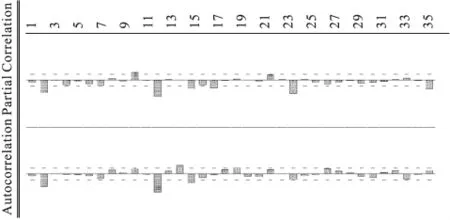
图3 序列ΔΔ12LnZt的相关图(下)和偏相关图(上)
首先考虑建立 SARIMA(2,1,2)(1,1,1)12模型,结果见表1,其中变量AR(2)的t=0.1917、P=0.8482>0.05,MA(2)的 t= -1.0041、P=0.3165 >0.05,两者都没有通过t检验。然后删除变量AR(2),尝试建立 SARIMA(1,1,2)(1,1,1)12模型,以及删除变量MA(2),尝试建立 SARIMA(2,1,1)(1,1,1)12模型。表 1 可见,SARIMA(1,1,2)(1,1,1)12模型和 SARIMA(2,1,1)(1,1,1)12模型的所有参数都通过了 t检验。而且,SARIMA(1,1,2)(1,1,1)12模型和 SARIMA(2,1,1)(1,1,1)12模型均有 27 个根,包括 7 个实根和20个复根,其倒数均小于1。
(3)模型的诊断检验
对 SARIMA(2,1,1)(1,1,1)12模型残差进行是否为白噪声的Q统计量检验,该残差序列的样本量n为213,最大滞后期m可以取[213/10]或[213],这里取22。Q22=18.534,P=0.356 >0.05,故不能拒绝残差序列为白噪声的原假设,检验通过。
对 SARIMA(1,1,2)(1,1,1)12模型残差进行是否为白噪声的Q统计量检验,该残差序列的样本量n为214,最大滞后期m可以取[214/10]或[214],这里取22。Q22=17.662,P=0.410 >0.05,故不能拒绝残差序列为白噪声的原假设,检验通过。
从表 2 可以看出,SARIMA(1,1,2)(1,1,1)12模型的 R2和调整 R2均比 SARIMA(2,1,1)(1,1,1)12的大,且对于AIC统计量和SC统计量,SARIMA(1,1,2)(1,1,1)12模型都比 SARIMA(2,1,1)(1,1,1)12模型要小。因此,SARIMA(1,1,2)(1,1,1)12模型拟合效果较好。

表1 各种SARIMA模型的检验结果

表2 两种模型的拟合优度比较
3.模型的预测
SARIMA(1,1,2)(1,1,1)12模型的表达式为:
(1-0.6249L)(1-0.2113L12)(1-L)(1-L12)log(Zt)=(1-0.6899L-0.2355L2)(1-0.9198L12)εt。该模型预测拟合图(见图4)显示,实际数据与预测数据相当吻合;对1990年1月至2009年12月的菌痢发病数进行回代预测,结果显示平均误差率为13.89%。

图 4 SARIMA(1,1,2)(1,1,1)12模型预测拟合图
根据所建模型对2010年1~5月的菌痢发病数进行短期预测,预测结果分别为:304、217、329、390和598,此5 个月的实际发病数分别为:277、262、268、414和601,其预测误差率分别为:9.75%、-17.18%、22.76%、-5.80%和-0.50%。
讨 论
目前,对传染病发病率进行预测时,常用的模型有曲线拟合、灰色模型、Markov模型、ARIMA/SARIMA模型等。其中,ARIMA/SARIMA模型将传染病流行过程中各种影响因素的综合效应统一蕴涵于时间序列中,这是其应用于传染病预测的一个突出优点。肠道、呼吸道和自然疫源性传染病的发病情况有着明显的季节性和周期性,如果不考虑这些因素的影响,做出的预测往往不准确,因此SARIMA模型在该领域有着广泛的适用性。该模型的建立已经有一套明确的准则,适用于各种复杂的时序模式,同时一些统计软件(如SAS、SPSS、Eviews等)为该模型的建立提供了有利条件,使其得到了广泛的应用。本文利用SARIMA模型对江苏省菌痢未来疫情动态和发展趋势进行预测,得到较好的预测效果,对存在季节性、周期性波动的传染病的预警具有指导意义。
江苏省菌痢的发病率从20世纪90代初的100.00/10万以上,下降至2009年的9.96/10万,但它仍居肠道传染病发病率的首位。通过SARIMA模型对江苏省菌痢2010年1~5月的月发病数进行了预测,发现我省菌痢的发病将继续呈下降趋势。但由于流行因素的广泛存在,作为一种高发病率的疾病,菌痢的发病率仍将维持在一个较高的水平,应继续实施现行防制策略,加强病原学监测、疾病预警工作。
ARIMA模型或SARIMA模型对疾病进行预测分析,有两大优点:①利用预测变量自身的变化规律建立模型,不考虑其相关因素;②明确考虑时间序列的非平稳性,通过取对数、差分等方法把序列平稳化后,再考虑建模问题。但是应用该模型应该注意:①至少需要50个以上的历史数据;②所建立的模型,不能作为永久不变的预测工具,只能用于短期预测。对于已建立的模型应不断加入新的实际值,以修正或重新拟合更优的模型〔6〕。
1.Helfenstein U.Box-Jenkins modelling in medical research.Stat Methods Med Res,1996,5(1):3-22.
2.Kao JJ,Huang SS.Forecasts using neural network versus Box-Jenkins methodology for ambient air quality monitoring data.J Air Waste Manag Assoc,2000,50(2):219-226.
3.樊欢欢,张凌云主编.Eviews统计分析与应用.北京:机械工作出版社,2009:227-228.
4.中国人民银行调查统计司主编.时间序列 X-12-ARIMA季节调整——原理与方法.北京:中国金融出版社,2006:59-60.
5.易丹辉主编.数据分析与EVIEWS应用.北京:中国人民大学出版社,2008:137-140.
6.漆莉,李革,李勤.ARIMA模型在流行性感冒预测中的应用.第三军医大学学报,2007,29(3):267-269.

