基于Pareto最优的多企业协同计划调度优化

张美华 李爱平 徐立云

同济大学，上海，201804

0 引言

在生产运作领域，调度主要是用于调配资源、合理安排生产作业顺序。调度优化过程就是寻找合理调度方案的过程，即对生产对象在不同的生产主体进行生产时，如何合理安排生产的匹配关系，以优化生产进程，在满足现有生产条件下，使生产收益最大化。在网络协同制造环境下，计划调度将涉及整个生产链中各个环节的任务规划、资源共享和分配，表现出更强的动态性、实时性以及协作性，各个目标所面对的不确定性和动态因素增大，调度问题的规模更大，调度解的相对稳定性也更难控制，调度问题不仅要实现调度的最优化，同时还要实现调度的敏捷性和动态性，其调度优化过程是一个复杂的随机多目标优化问题［1］。不同于单目标优化问题，多目标优化问题极少存在绝对最优解，而是存在一个最优解集合，即Pareto最优解集或非支配解集。

目前在网络协同制造环境下多企业协作的多目标调度优化问题的研究方面，国内外学者做了一些研究，也提出了很多相关的模型和算法。如文献［2］建立了以加工时间、加工成本和加工质量为目标的多任务加工资源优化配置多目标模型，并进行了基于遗传算法的求解。针对多个具有供需关系的制造工厂和多个地域分散的客户组成的供需网络，文献［3－5］建立了多目标生产计划模型，提出了禁忌搜索与后向启发式方法相融合的B－TS算法、线性规划法、模糊规划与遗传算法来解决多目标多工厂生产计划问题。文献［6］针对网络化协同制造中的任务分配问题，建立了以制造任务完成时间、完成成本和产品工艺质量为目标的多目标优化模型，提出了模型求解的改进遗传模拟退火算法。上述方法都是采用经典的加权算法将多目标问题转化为单目标问题进行求解，需要根据用户对不同目标的偏好程度设置系数值。最近有学者提出了基于Pareto概念的多目标进化优化算法，该算法通过模拟生物自然选择和自然进化，不依赖于决策者对目标函数的偏好，具有隐含的并行性和全局解空间搜索的能力，并且一次运行可得到多个Pareto最优解或近似解供用户选择，非常适合求解多目标优化问题，受到越来越多的关注。国内外学者在这方面已经做了很多的研究，提出了大量多目标进化算法，主要包括 VEGA、NPGA、MOGA、SPEA2和NSGA－Ⅱ等算法。其中文献［7］提出的NSGA－Ⅱ（non－dominated sorting genetic algorithmⅡ）算法，既有良好的收敛性和分布性，又具备较快的收敛速度，被国内外学者广泛引用。如文献［8］提出了一种改进的MOGA多目标进化算法，该算法主要用于考虑各机器间的工艺协同性时对分布式制造系统的工艺计划和调度进行求解。文献［9］建立了整体运行成本与生产负荷最小化的多目标函数优化模型，分析了其时序约束条件，并采用NSGA－Ⅱ算法进行了分析求解。文献［10］建立了同时考虑整体生产成本和各企业设备生产能力的虚拟企业多目标生产计划模型，并利用改进的多目标进化算法NSGA－Ⅱ对该模型进行求解。上述研究的共同不足是，都没有考虑实际生产运作过程中各协作企业生产与运输能力对计划调度的影响。因此，本文基于Pareto最优概念，针对多企业协同生产链实际运作过程，建立了一种考虑综合成本和完工时间的多企业协同计划调度多目标优化模型，并根据实际问题对多目标进化算法NSGA－Ⅱ进行优化设计来求解协同制造过程中的计划调度问题。

1 协同计划调度问题分析

协同生产链由分布的协作生产企业提供的生产服务按一定顺序组合，即协作生产企业为完成某种产品的生产任务，而形成的彼此之间的上下联系关系，这种协作关系主要体现在生产过程间的合作与协同。由于生产任务之间的执行次序约束关系，使得这些协作企业的生产活动相互联系又相互制约。因而，在协同制造过程中，生产链上所有企业之间的计划调度与协调非常重要。本文采用有向无回图DAG来抽象表示各子任务间的时序约束关系。如图1所示，S为一个虚拟起始点，与无前驱子任务约束的子任务节点相连，虚拟起始点不占用任何操作时间及操作成本。令G＝（T，E），其中G是子任务集T的依赖关系图，子任务集合T＝｛T1，T2，…，Tn｝为n个子任务的集合，一个子任务Ti就是图1中的一个节点，E是任务依赖关系图中的有向边的集合，表示节点间的关系，即各子任务间的约束关系，各任务的启动和执行必须满足一定的时间和顺序约束。（Ti，Tj）∈E（i，j＝1，2，…，n），表示在子任务Ti没有完成之前，任务Tj不能执行。

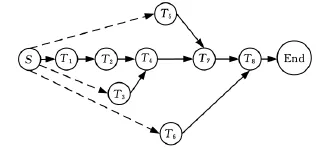
图1 子任务约束关系图

在协同生产链的实际运作过程中，由于协同生产链中各协作企业地理位置分散，考虑到各协作企业之间的运输时间、运输成本，以及生产任务之间的执行次序约束关系，协同计划调度优化问题求解变得非常复杂。当任何一个子任务选择的协作企业改变时，都会使得该协作企业与相关联协作企业之间的运输时间和运输成本发生变化，对前后子任务的协作企业选择产生影响，进而对其余所有的子任务选择协作企业产生影响，最终影响整个协同生产链的总成本、总时间等，即任何一个子任务选择的协作企业发生改变可以影响整个协同计划调度优化方案的结构。此外，在多企业协作制造模式中，协作企业具有较高的自主性和自治性，企业根据需要可以参与多条协同生产链，对整个协同生产链而言，每一个协作企业的生产与运输能力本身都具有一定的不确定性，这是由于协同生产链的形成机制造成的。

2 协同计划调度多目标优化模型

2.1 问题描述

针对在企业协同生产链实际运作过程中，各协作企业的生产与运输能力的不确定性对协同计划调度的影响，通过综合考虑协同生产链中具备生产能力，并且愿意承担生产任务的各协作企业的生产时间、生产成本，以及具有子任务时序约束关系的各协作企业间的运输时间、运输成本等指标，建立一种考虑综合成本和完工时间的多目标计划调度优化模型，以便从众多的计划调度方案中选择出整体最优的协同计划调度方案，即为制造任务选择出最优的协作企业组成协同生产链，并按给定的交货期完成任务。

前提条件假设：

（1）本文主要研究协同生产链企业间调度合作，而不涉及各企业内部调度流程。

（2）每个子任务的开始时间依赖于其他一些子任务的完成（时序约束），生产任务在执行期间不中断。

（3）每个子任务只交由一个生产企业完成。

（4）忽略企业的订货及企业内部的库存成本，仅考虑企业间的生产成本、时间及运输成本。

2.2 协同计划调度多目标优化模型

设协同生产链内共有协作企业m个，某一制造任务可以分解为具有时序约束的子任务n个。对于任一子任务Ti（i＝1，2，…，n），有 mi（mi∈m）个协作企业可以完成。D为整个任务的交货期。最后一个子任务Tn的完成时间dn为整个任务的实际完工时间。

2.2.1 决策空间

协同计划调度方案可以描述为：P＝｛Mij，STij，FTij，Cij，dn｝，即包含了所有子任务的最优生产企业、开始生产时间、完工时间、综合成本，以及交货期等参数。

可选协同计划调度方案集合为

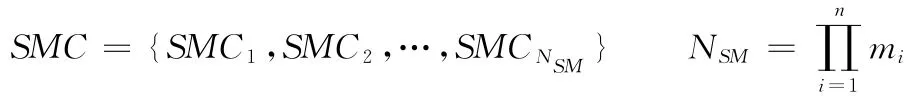
式中，NSM为可选协同计划调度方案的总数量。

子任务集合为T＝｛T1，T2，…，Tn｝；子任务Ti的备选协作企业的集合为Mi＝｛Mi1，Mi2，…，Mij｝，（j∈ ｛1，2，…，mi｝，i∈ ｛1，2，…，n｝）；定义决策变量：

定义子任务约束：

2.2.2 协同计划调度多目标优化模型

面向协同生产链的协同生产计划调度优化目标是使整个任务的制造过程最优，即整个协同生产链的综合成本最低，任务完工时间最短。

其对应的多目标优化模型为：

（1）综合成本最低。数学表述式为

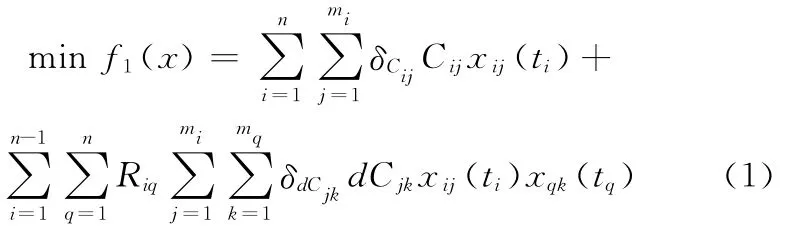
式中，Cij为企业Mj完成子任务Ti的生产成本；dCjk为存在时序约束关系的2个子任务所选中企业Mj、Mk间的运输成本；δCij为企业Mj生产成本的动态不确定因子；δdCjk为企业Mj、Mk间运输成本的动态不确定因子。

（2）任务完工时间最短。数学表述式为

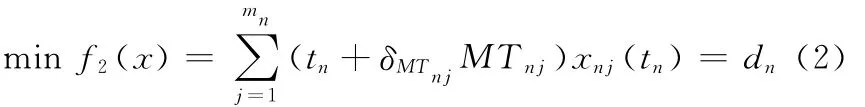
每个任务的完工日期为

式中，MTij为子任务Ti在企业Mj的生产时间；dTjk为存在时序约束关系的2个子任务所选中企业Mj、Mk间的运输时间；δMTij为企业Mj生产子任务Ti的生产时间的动态不确定因子；δdTjk为企业Mj、Mk间的运输时间的动态不确定因子。

（3）约束条件。

①任务选择约束：

式（4）表示每个子任务必须选择且只能选择一个企业进行生产。

②任务时序约束：

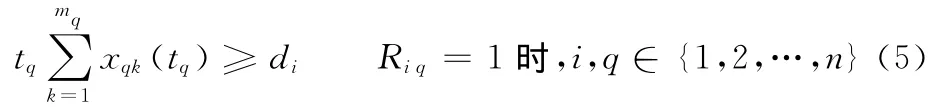
式（5）表示对有时序约束关系的子任务，前一子任务完工后，后一子任务才能开工。

③资源约束：

式（6）表示同一企业同一时间只能加工一个子任务。

④总交货期约束：

3 基于Pareto最优的NSGA－Ⅱ算法

3.1 基于Pareto最优的NSGA－Ⅱ算法原理

NSGA算法［12］是基于个体的等级按层次来分类的，将非支配排序法引入遗传算法，在选择配对之前，先按解个体的非支配性进行排序。NSGA－Ⅱ是对NSGA算法的改进，采用了快速的非支配性排序方法（fast－nondominated－sorting），定义的拥挤距离（crowding distance）用于估计某个点周围的解密度，以取代适应值共享。NSGA－Ⅱ有效地克服了NSGA的三大缺陷，使得其计算复杂性降低，具备最优保留机制及无需确定一个共享参数，从而进一步提高了计算效率和算法的鲁棒性。

本文基于Pareto最优解思想，利用NSGA－Ⅱ多目标优化算法来探讨多目标协同计划调度的优化方法。改进的NSGA－Ⅱ算法流程如图2所示，在算法的整体框架内，根据问题的实际要求设计了有效的编解码方式和遗传操作，集成了局部变异种群重复个体和自适应精英保留策略，用以保证算法的收敛性和多样性。

3.2 基于NSGA－Ⅱ的调度优化算法设计

3.2.1 染色体编码与解码

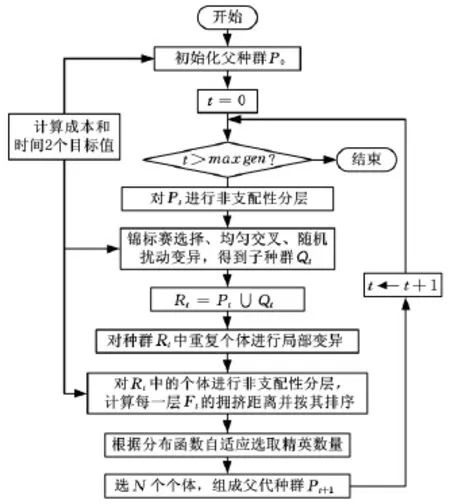
图2 改进的NSGA－Ⅱ算法基本流程图

编码的好坏直接影响到进化的方法以及进化运算的效率。协同计划调度的目的是进行子任务的分配与时间的优化，本文在编码过程中只考虑子任务分配问题，至于时间的制定与优化，将由解码过程分析实现。在一般情况下，与每个子任务相对的协作企业的数量都是不等的，因此采用基于排列的实值编码，每条染色体代表一个调度选择方案。

编码规则如下：

（1）将子任务编号为1，2，…，n。

（2）一个个体由n个基因组成，每一基因的位置与子任务号相对应。

（3）将所有的协作企业进行编号，不同的子任务对应的协作企业数mi不同，一个协作企业可以申请多项子任务，但是一项子任务只能分配给一个协作企业。

（4）初始个体的每个基因位上的值，在相互排斥的第i个子任务的所有备选协作企业的集合｛1，2，…，Mi｝之中随机产生，染色体结构如图3所示。即一条染色体中基因位用来表示子任务，而对应的基因值则用来表示该子任务所选择的协作企业。如第4位的“7”表示：子任务T4由协作企业M7来完成。

图3 染色体结构图

解码过程也是对各协作企业调度的过程，以确定各子任务在协作企业的开始和完工时间，并得到整个任务的总交货时间。在解码过程中，要根据子任务约束Riq，主要保证某一子任务开始生产时所有的关联子任务已经完成。编码方案的解码分为两步：首先，将染色体根据基因值依次转换为子任务的协作企业序列；其次，依照协作企业序列查找对应子任务的生产时间、运输时间，根据约束式（5），计算该子任务的上一个相关联约束子任务的完成时间，取较大者为该子任务的最早开始时间，如果该子任务前面无约束子任务时，根据约束式（6）查看该子任务对应的协作企业的当前完工时间，取其作为该子任务的开始时间。重复此过程，直至将所有子任务分配给各自的协作企业为止，最终获得各子任务的开始时间和完工时间以及总完工时间，从而得到一个协同计划调度方案。

3.2.2 快速非支配性排序方法和精英策略

（1）快速非支配性排序。在NSGA－Ⅱ算法中，个体的适应度包括最优解的非支配等级和拥挤距离。根据解码结果及式（1）、式（2），计算每个个体相应的f1（x）和f2（x）目标函数值，以此作为非支配性分层的依据，对最优解集中的解根据目标函数值的大小进行排序，并赋予相应的非支配等级。然后对每一层进行拥挤距离的排序。拥挤距离用于估计一个解周围其他解的密集程度。设每一个体i的支配等级属性和拥挤距离属性分别为irank和idis，随机选取2个个体并进行比较，保留一个优良个体，淘汰另一较差个体。其过程为

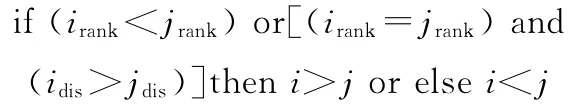
在NSGA－Ⅱ算法中，由于个体适应度值分配机制和构造新种群时的个体选择机制，合并种群时容易产生一些重复个体被赋予了相同的适应度值而被选择进入了下一代种群中，使得算法对目标空间的搜索效率变低，而且这种个体重复的现象不会随着算法的运行而消失，在最终的输出解集里面仍然有一定数量的个体在目标空间是相互重复的。因此算法所得解集的分布性受到影响，解集质量不够理想。在本文中，每次在种群合并后的分层排序阶段，为了保持种群的个体多样性，首先，对合并后的种群Rt检验其是否具有重复的个体，若有，则对该重复个体进行局部变异，直至种群Rt中的个体各不相同，并由式（1）和式（2）计算所有新个体的目标函数值。

（2）精英策略。精英策略即保留父代中的优良个体直接进入子代，这种方法在保持好的个体及加速向Pareto前沿收敛方面都有很好的表现。但在NSGA－Ⅱ算法中由于没有限制精英解的范围，使得种群在进化到某一代以后，种群中的所有解都是精英，随后各代的操作都将在精英解中进行，非精英解无法参与其中，降低了解的多样性，使得全局解的搜索速度减慢并最终导致种群过早收敛到局部Pareto解。

因此，为了确保个体的多样性及搜索向全局Pareto优解收敛，自适应地限制当前精英解集的范围，从而使非精英解集也能平等的参与到新种群的操作就显得尤为重要。因此，在组成父代种群时，我们采用文献［13］的分布函数自适应地选取精英数量，从而更好地保持种群的多样性。其分布函数为

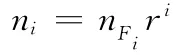
式中，ni为从非支配集合Fi中选取的个体数；nFi为非支配集合Fi中的个体数；r为自适应精英算子，r∈（0，1）是一个可以由用户来自定义的参数。

从分布函数可以看出，等级1（i＝1）中所选取的精英数的比例最大，而等级1中的解是当前种群中最好的最优解，这充分照顾到了精英解，使得遗传操作中具有较多的精英解参与，同时也使得非精英解参与到新种群的操作中。随着等级数i值的增大，每个非支配层中所选取的精英解比例依次减少，这对于各个等级都是公平的，也体现了“适者生存，优胜劣汰”的思想。

3.2.3 遗传算法算子的设计

（1）选择操作。这里采用二元锦标赛选择算子，从父代种群Pt＋1中随机选择2个染色体，按排序等级值越小越优先，同一等级则拥挤距离越大越优先的原则，采用随机锦标赛的形式来产生优选种群。

（2）交叉操作。根据协同计划调度的染色体编码方案特点和约束，在本文中，优化算法将采用均匀交叉算子，即将每个点都作为潜在的交叉点，随机产生与个体等长的0－1掩码，掩码中的片断表明了哪个父个体向子个体提供变量值，然后根据该模板对2个父代个体进行交叉，得到2个新个体，这样保证产生的每个子个体都是可行解，可提高算法的搜索效率，保持种群的多样性。

（3）变异操作。由于协同生产链中每个子任务都可以由多个协作企业来完成，这里采用随机扰动算子，选定一个个体作为父个体，随机选择一个基因位，被选中个体的基因值用协作企业集合Mi中随机选取的整数替代。

4 仿真应用

以某柴油机厂为例，某一任务可以分解为8个有时序约束关系的子任务，协同生产链由10家备选协作企业组成，各子任务约束关系如图1所示，则子任务约束矩阵中：R12＝1，R24＝1，R34＝1，R47＝1，R57＝1，R68＝1，R78＝1。子任务Ti的备选企业 Mi 集合为 T1：｛M1，M3，M4，M6，M10｝，M1＝5；T2：｛M2，M3，M5，M8｝，M2＝4；T3：｛M1，M2，M3，M4，，M8，M9｝，M3＝6；T4：｛M2，M5，M7，M9｝，M4＝4；T5：｛M3，M4，M6，M8，M10｝，M5＝5；T6：｛M1，M5，M8，M10｝，M6 ＝4；T7：｛M4，M7，M9｝，M7＝3；T8：｛M2，M5，M7，M8，M10｝，M8＝5；交货期为60天。

其中各备选协作企业的生产成本和生产时间如表1所示。

表1 各备选协作企业的生产成本（万元）和生产时间（d）

各备选企业之间的运输时间dTij和运输成本dCij可分别表示为

用MATLAB 2009进行仿真，初始种群大小为100，迭代次数为100次，取交叉概率Pc＝0.7，变异概率Pm＝0.05，自适应精英算子r＝0.9。

初始种群个体的分布及Pareto最优解集如图4、图5所示。

图4 初始种群的分布图

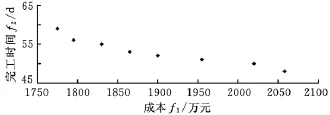
图5 协同计划调度Pareto最优解集

从图4、图5可以看出，初始种群中的个体散乱分布于一个较大的范围内，而当算法结束时，个体分布已经集中到了最优解所存在的区域内，所得最优解集在Pareto前沿分布均匀，具有良好的多样性和收敛性。最优解集所对应的一组协同计划调度优化方案如表2所示。

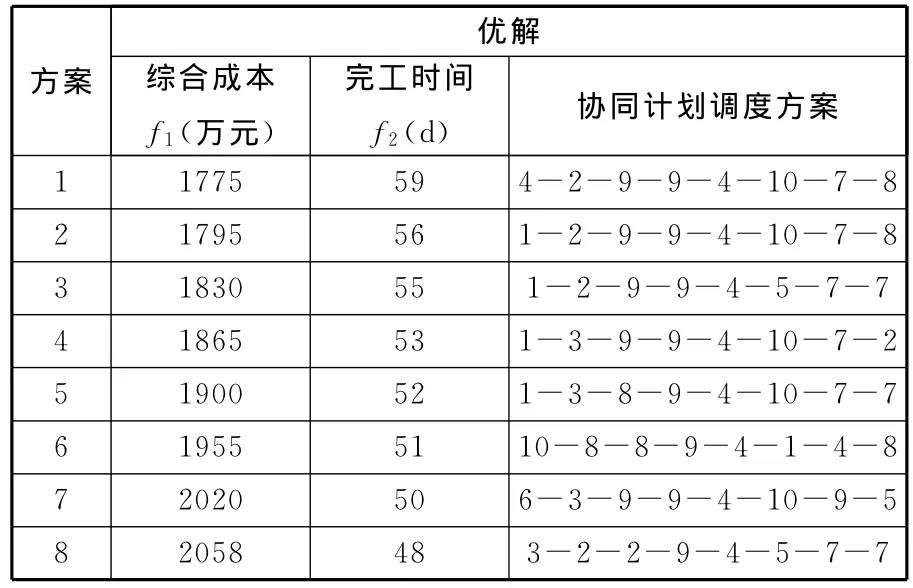
表2 协同计划调度优化方案

决策者可根据自己的偏好或结合生产实际情况，选取一个方案作为优化调度结果。此外，由表2也可以看出，方案4和方案5具有相近的目标值，选择的企业也相似，因此，当实际生产中遇到任何变动时，还可以进行快速的反应和处理，提高了企业协同计划调度的灵活性。图6所示为选取方案4时对应的协同计划调度甘特图，数字表示任务和执行的企业。

图6 协同计划调度甘特图

为验证算法在解决协同生产计划调度多目标优化问题上的性能，同时采用VEGA和SPEA2算法在参数设置相同的情况下进行计算比较。表3所示为应用NSGA－Ⅱ算法与VEGA和SPEA2算法各运行30次的对比结果。计算结果表明，本文算法具有计算耗时少，解的性能较好，对于求解协同制造计划调度的多目标优化问题能取得良好的效果。

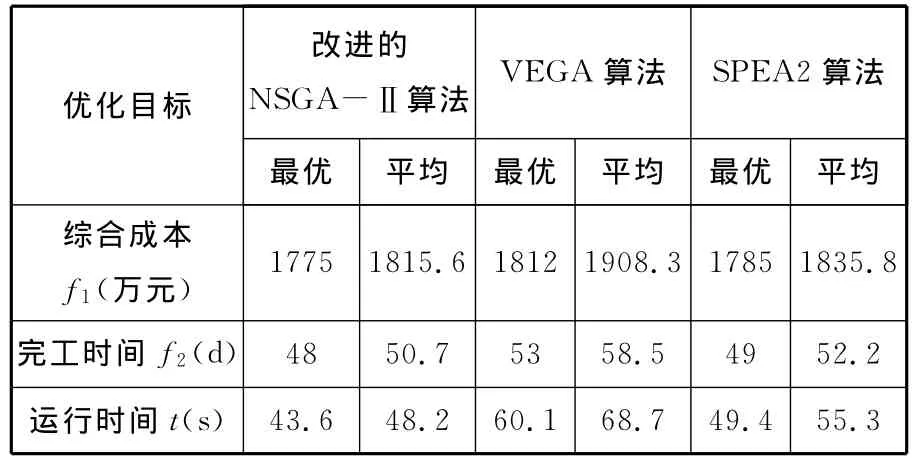
表3 算法性能比较

5 结论

针对在企业协同生产链实际运作过程中，各协作企业的生产与运输能力的不确定性对协同计划调度的影响，本文以综合成本和任务完工时间为优化目标，在子任务执行时序、总任务执行时间、协作企业资源约束下，建立了一种适合多企业协同计划调度的多目标优化模型。为了从众多的计划调度方案中选择出整体最优的协同计划调度方案，本文利用Pareto最优概念的NSGA－Ⅱ多目标进化算法进行求解，设计了有效的编解码方式和遗传算子操作规程，并通过局部变异种群重复个体改善解集的质量，提高算法的搜索效率，自适应地选取Pareto最优解集的精英数量，更好地保持了种群的多样性和全局最优解的收敛性。所建立的多目标优化模型使多企业协同生产链整个任务的制造过程最优，实现了节约成本与提高协作企业效益的目标；采用多目标优化算法获得的Pareto最优解集，有利于决策者根据优化目标的重要程度和生产过程中的实际情况做出相应的决策选择。最后通过仿真实例，验证了算法的有效性。

［1］高阳，曾小青，周伟.多智能体协同生产管理及其系统［M］.北京：清华大学出版社，2006.

［2］尹胜，尹超，刘飞，等.多任务外协加工资源优化配置模型及遗传算法求解［J］.重庆大学学报，2010，33（3）：49－55.

［3］苏生，战德臣，李海波，等.不确定需求和能力约束下的多目标多工厂生产计划［J］.计算机集成制造系统，2007，13（4）：692－697.

［4］Al－e－hashem S M J，Malekly H，Aryanezhad M B.A Multi－objective Robust Optimization Model for Multi－product Multi－site Aggregate Production Planning in a Supply Chain Under Uncertainty［J］.International Journal of Production Economics，2011，134（1）：28－42.

［5］Aliev R A，Fazlollahi B，Guirimov B G，et al.Fuzzy－genetic Approach to Aggregate Production－distribution Planning in Supply Chain Management［J］.Information Sciences，2007，177（20）：4241－4255.

［6］郭志明，莫蓉，孙惠斌，等.改进GSA算法在协同制造任务分配中的应用［J］.计算机工程与应用，2011，47（14）：210－213.

［7］Deb K，Pratap A，Agarwal S，et al.A Fast and Elitist Multiobjective Genetic Algorithm：NSGA－Ⅱ［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197.

［8］Zhang Wenqiang，Gen M.Process Planning and Scheduling in Distributed Manufacturing System U－sing Multiobjective Genetic Algorithm ［J］.IEEE Transactions on Electrical and Electronic Engineering，2010，5（1）：62－72.

［9］Cheng Fangqi，Ye Feifan，Yang Jianguo.Multi－objective Optimization of Collaborative Manufacturing Chain with Time－sequence Constraints［J］.The International Journal of Advanced Manufacturing Technology，2009，40（9／10）：1024－1032.

［10］高阳，罗根.不确定环境下虚拟企业生产计划多目标优化模型研究［J］.组合机床与自动化加工技术，2009（1）：97－100.

［11］王小平，曹立明.遗传算法－理论、应用与软件实现［M］.西安：西安交通大学出版社，2002.

［12］Srinivas N，Deb K.Multi－objective Optimization Using Nondominated Sorting in Genetic Algorithms［J］.Evolutionary Computation，1994，2（3）：221－248.

［13］杨善学，王宇平.基于Pareto最优和限制精英的多目标进化算法［J］.计算机工程与应用，2007，43（2）：108－110.