公路跑道粉砂土路基地震液化及稳定性研究

郑元勋，黄静卿

（郑州大学 水利与环境学院，河南 郑州450002）

0 引言

公路跑道兼有交通战备项目的应急机场功能和高速公路项目的地面交通功能，公路跑道项目的修建是一项社会经济发展规划与国防交通运输保障相结合的工程，是在交通建设贯彻国防要求的具体体现.粉砂土路基的稳定性对高路公路及公路跑道的服务质量及使用寿命具有重要的影响，且粉砂土在动力及地震荷载作用下易发生液化现象，进而导公路及公路跑道的破坏［1－5］.研究表明，目前，国内外针对粉砂土的研究多集中在粉砂土路基施工技术及检测方法［6－10］、粉砂土路堤累积变形及变形指标和粉砂土路基冻胀性能的研究等［11－13］，而针对粉砂土路基地震液化及稳定性研究、尤其是涉及到公路跑道粉砂土路基地震液化及稳定性的研究相对匮乏，因此，开展公路跑道粉砂土路基地震液化及稳定性研究具有非常重要的理论和现实意义.

1 公路跑道粉砂土路基数值模型的建立

1.1 模型参数设置

以郑民高速公路为例，根据勘察报告，场地钻探深度范围主要由粉砂、粉土组成，本区第①②层为局部可液化地层，综合判定该场区液化等级为轻微.

开封市抗震设防烈度为7度，设计基本地震加速度值为0.1 g，设计地震分组为第一组，拟建物抗震设防类别为丙类.20 m内波速在140～250 m／s，场地类别为3类，场地特征周期为0.45 s.根据场区地质、地形、地貌条件判别，该区属建筑不利地段.地下水位埋深1.7～1.8 m，年变幅1 m左右.

取泊松比μ＝0.35，根据勘察得到的剪切波速反算得路基土剪切模量G＝30.38 MPa，体积模量B＝91.14 MPa，同理取路堤土剪切模量G＝35.67 MPa，体积模量B＝107.02 MPa.根据经验取路堤土的黏聚力c＝20 k Pa，摩擦角φ＝28°，路基土的黏聚力c＝10 k Pa，摩擦角φ＝23°.

1.2 模型尺寸确定、边界条件处理

计算时取路宽28.5 m，路堤高3 m，坡度1∶3.计算域水平方向从路堤坡脚向两侧各取45 m，向下取25 m.考虑到场地类别为3类，特选取地震波输入为：1994年6月17日的NORTHRIDGE EARTHQUAKE（图1），并峰值分别调整0.1 g.

计算时，第一步先施加固定边界约束，保证模型在平面应变下进行静力计算，即仅在重力作用下算至平衡.图2为计算网格，图3和图4分别为初始孔压和初始竖向应力云图.

数值模拟采用瑞利阻尼.瑞利阻尼需要设置两个参数：模型的临界阻尼比和基频（一阶固有频率）.模型固有频率的确定可以通过对模型在只有重力加速度的情况下进行动力模拟，显示在一定时步内模型中某点的速度或位移关于时间的曲线，即估计得到模型固有频率的大约值.这里取主频2.22的0.5%作为瑞利阻尼参数，并取计算时间40 s.然后将地震动荷载的加速度时程离散为数据表（Table）的形式.由于本模型底面设置了完全不反射的安静边界，所以需将加速度时程经频域一次积分得到速度时程，然后转换为应力时程从模型底面输入.

判断液化区域时，当计算单元的有效应力小于等于零或动抗剪强度小于动剪应力时即可认为该单元发生液化.

2 库伦模型的地震分析

整个计算域内的土体采用库仑模型来处理.地震作用导致的动态体积变化能使这些材料中的孔隙水压力发生改变，然而，也能因颗粒重组导致孔隙水压力不发生变化，为了能使孔隙水压力随体积而改变，必须指定水体积模量的实际值，本文设置为2×109Pa，这样设置考虑了土体中所含空气的影响.此阶段，假定动态激励过程存在的时间远小于孔隙水压力消散所需时间，因此此阶段不使用地下水流动模型.

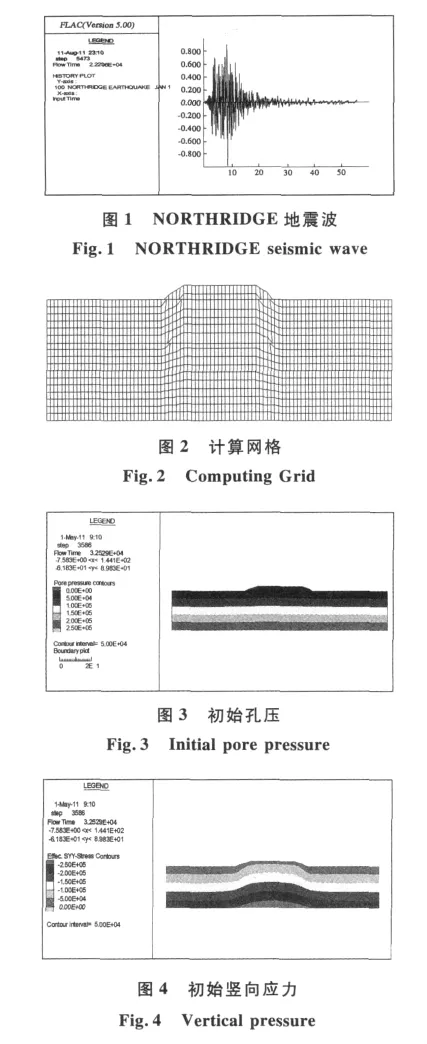
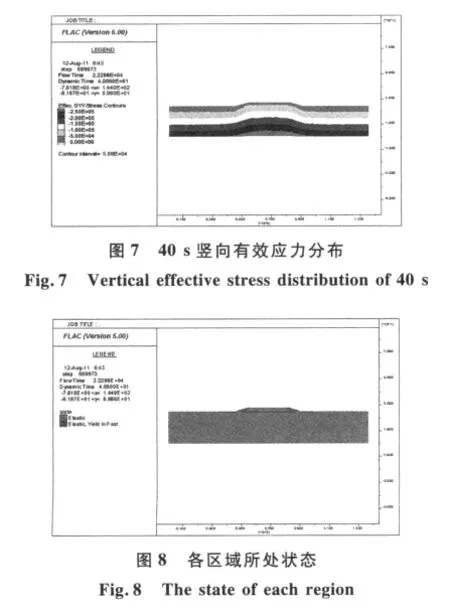
图5为路堤底部中点的超孔压随时间的变化图.该图表明，路基内孔压累积不多，25 s后已几乎不再变化.图6为路面中点相对于模型底部的水平位移和竖向位移.很明显，40 s后路面位移趋于零.图7为计算结束（40 s）时竖向有效应力分布云图.该图表明，整个计算域内有效应力都处于压缩状态，按照土力学的定义，即有效应力都大于零，没有出现孔隙压力超过（或等于）正应力的情况，即不会出现液化现象.但图8表明，路堤坡脚处附近在地震过程中可能瞬时处于屈服状态.

3 Byrne模型的地震分析

将原地面下6 m内路基土改为Byrne液化模型，参数参照标准贯入试验取值，当标准锤击数小于15 击时，Byr ne参数为：C1＝0.294 7，C2＝1.357.

图9为路堤底部中点的超孔压随时间的变化图.很明显，路基内孔压累积较多，大约在12 s时，此处累计超孔隙水压约55 k Pa；以后略有消散，但在计算结束（40 s）时仍有约50 k Pa，即大部分都没有消散.图10为40 s内路面中点相对于模型底部的水平位移和竖向位移变化情况.该图表明，约6 s后，路面产生了竖向的永久变形，并且该竖向变形在6～12 s内随时间而迅速增大，以后渐趋稳定，计算结束时，其值约为8～9 mm.

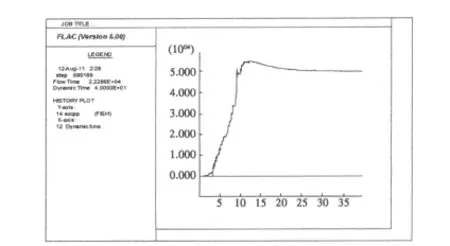
图9 路堤底部中点的超孔压随时间的变化图Fig.9 The versus time diagram of the excess pore pressure of the midpoint of the embank ment bottom

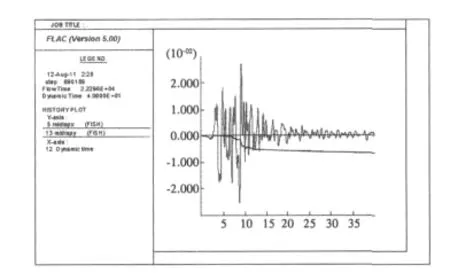
图10 40 s内路面中点相对于模型底部的水平位移和竖向位移Fig.10 The road midpoint relative to the horizontal displacement and vertical displacement of the model bottom within 40 s

图11 为40 s时计算域内的竖向有效应力分布云图.该图表明，路堤下较大范围内竖向有效应力值偏小，有液化可能.这也可从示于图12的计算域竖向对称线上的水平向有效应力分布曲线得到验证：在路面下9 m以内水平向有效应力不足5 k Pa.

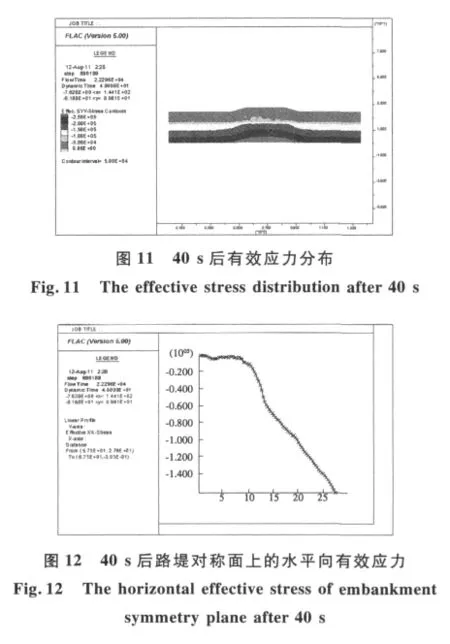
4 地震强度影响分析

为考察地震强度的影响，这里也分别将地震加速度峰值调整为0.05 g和0.2 g进行了计算.

图13～16为加速度峰值为0.05 g的计算结果.图13表明，路堤内孔压在约12 s内累积很快，但随后基本稳定，直至计算结束，但最大仅约24 k Pa，不足加速度峰值为0.1 g时的一半.图14表明，路面竖向永久位移很小.图15表明，尽管计算域内竖向对称面上的水平向有效应力在路面下3～9 m内有所减小，但都仍然较大.图16表明，路堤边坡在坡面附近有可能瞬时出现屈服现象，但整体看，破坏区范围远没有加速度峰值为0.1 g时大.

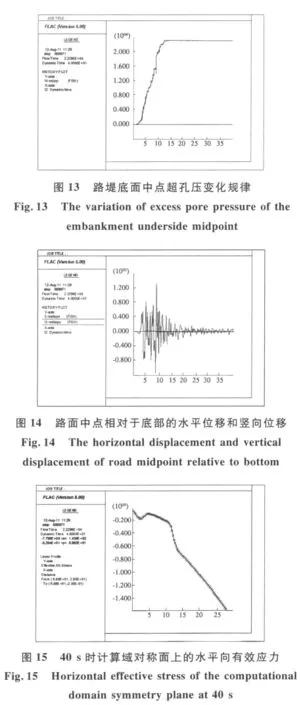
图17～图19为加速度峰值调整为0.2 g时的计算结果.图17为路堤底部中点超孔压的累积变化规律曲线.该图与加速度峰值为0.1 g的规律相似，即在约12 s时孔压累积到最大值约53 kPa，以后孔压稍有消散并趋于稳定，最后约为44 k Pa.图18表明，路面产生了较大的永久变形，其中路面中点竖向沉降最大可达约45 mm，约为加速度峰值0.1 g时的5.5倍.图19表明，路堤内部以及路基下一定范围内的水平向有效应力明显偏小，特别地，对称面上路面下9 m以内的水平向有效应力值都没有超过10 k Pa，这说明，存在液化的可能.

5 结论

（1）地震分析表明：当只考虑路堤下粉土为库伦模型时，路基不会出现液化，但是路基坡脚处可能出现瞬时屈服.

（2）当考虑路堤材料为液化模型时，路面有可能处于受拉状态，路堤底部有可能屈服，路基土有可能产生液化.

（3）随着加速度峰值的增加，路堤内拉力区和屈服区的范围增大，液化出现的可能性也增大.特别地指出，当地震加速度达到0.1g时，并不能完全排除路基土液化的可能性.

［1］ CHEN H J，LIU S H.Slope failure characteristics and Stabilization methods［J］.Canadian Geotechnical Jour nal，2007，44（4）：377－391.

［2］ ZHENG Yuan－xun，KANG Hai－gui，Cai Yingchun，et al.Effects of temperat ure on the dynamic properties of asphalt mixtures［J］.Jour nal of Wuhan University of Technology－Mater.Sci.Ed.，2010，25（3）：534－537.

［3］ 程培峰，徐云哲.基于ABAQUS的包边粉砂土路堤边坡稳定性分析［J］.公路，2011（11）：21－24.

［4］ 蒋鑫，凌建明，谭炜，等.高速公路填砂路基边坡稳定性分析［J］.铁道工程学报，2008（9）：1－5.

［5］ 中华人民共和国交通部.JTJ E60－2008公路路基路面现场测试规程［S］.北京：人民交通出版社，2008.

［6］ 王峰.粉砂土路基的成型工艺与现场检测技术的研究［D］.沈阳：东北林业大学土木学院，2010.

［7］ 李强.路基路面检测技术与质量控制［D］.西安：长安大学交通学院，2002.

［8］ 申爱琴，郑南翔，苏毅，等.含砂低液限粉土填筑路基压实机理及施工技术研究［J］.中国公路学报，2000，13（4）：12－15.

［9］ 林龙.粉砂土的压实特性与路堤沉降预测方法研究［D］.长沙：湖南大学土木学院，2008.

［10］张宏博，黄茂松，宋修广.循环荷载作用下粉砂土路基累积变形试验研究［J］.公路交通科技，2009（9）：22－25.

［11］严战友，赵国芳，张永满.砂性土高速公路路基力学与变形指标的分析［J］.公路交通科技：应用技术版，2009（3）：90－93.

［12］肖军华，周顺华，韦凯.列车振动荷载下铁路粉土路基的长期沉降［J］.浙江大学学报：工学版，2010，44（10）：1913－1918.

［13］程培峰，宇德忠，徐云哲.季冻区粉砂土冻胀试验及路基冻胀模型［J］.中外公路，2011（2）：20－22.