结合图论与地理信息系统的供水管网分区优化
刘 俊,俞国平
(1.同济大学 环境科学与工程学院,上海200092;2.启东市住房和城乡建设局,江苏 启东226200)
随着城市化进程的加速,供水管网规模也随之扩大,大型的供水管网具有成千上万千米的配水管线,导致发现和定位漏损十分困难.近20 多年来出现了一种新的供水管网漏损管理结构,即将管网划分为若干个分区(DMAs),便于分别确定不同区块的漏损,并将主要的降低漏损工作集中在漏损严重区域,从而显著降低管网漏损.DMAs既有优点,又存在缺点[1].总体上供水系统分区后带来的漏损控制优势大于可靠性降低导致的风险,而且可以通过合理的管理降低分区带来的不利影响.
复杂管网如何实现分区是项复杂的工作.为了降低分区的复杂性,一般需要逐级分区[2].分区方法主要包括人工经验分区、拓扑结构分区和智能优化分区.人工经验分区主要依赖管理者对供水管网的深入理解,运用日常管理运行中积累的经验进行分区,并应用管网模拟验证分区的合理性.Grayman等[3]以人工经验方法通过添、减、修改现有管段调整阀门开启度进行管网的分区设计.Swamee等[4]使用流量路径概念进行多水源供水管网分区.黄茂林[5]综合考虑各种分区方案,通过管网模拟确定了推荐方案.人工经验分区具有较大的主观性,由于供水管网的规模大、复杂程度较高,不可能对供水管网的性能、结构完全了解,因而得到的分区可能会有缺陷.
拓扑结构分区利用拓扑学、图论等知识,从结构上对供水管网进行深入研究,继而提出分区方案.Tzatchkov等[6]使用图论中的深度优先搜索算法和宽度优先搜索算法并借助水质示踪剂模拟实现管网分区.Sempewo等[7]利用分布式计算中图论分割原理获得相同大小的管网区域以控制漏损.Nardo等[8]提出了基于图论的设计决策方法进行管网分区.Perelman等[9]利用延时模拟,根据管段流向是否变化,通过图论搜索算法得到不同节点的聚类,并使用地理信息系统(GIS)将结果可视化用来指导分区.阎立华等[10]利用图论算法确定多水源管网各水源的供水范围.刁克功[11]提出了基于拓扑结构演化的分区方法.拓扑结构分区从管网结构的角度研究分区,并借助经验及考虑多种影响因素即工程约束条件,能够迅速地对大型管网实施分区工作,利用管网模拟调整分区方案,使其满足供水要求.
智能优化分区借助优化算法完全由计算机模拟确定管网分区方案.Lzquierdo等[12]利用配水系统的分布特性,使用多代理系统进行配水管网分区.Herrera等[13]利用管网信息矩阵转换与半监督核波谱聚类方法进行分区.Awad等[14]利用遗传算法进行DMAs设计,同时确定了时间调节降压阀的位置和设置.智能优化算法是一种比较有前景的分区方法,但由于影响管网分区的因素很多,通常的单目标或双目标优化算法获得的分区方案往往不理想.另外,还有许多因素如技术、经济要求难以通过数学模型描述,限制了智能优化分区的应用.
本文提出了利用图论和GIS进行供水管网分区优化的方法,通过图论中最短路径算法得出供水管网水源到各节点的最短水力路径和最短耗散路径,借助GIS可视化供水管网最短路径树状结构,该结构可以简化供水管网结构,方便地进行供水管网分区设计,并将该方法应用到实际供水管网分区中,实现了复杂供水管网分区设计的工作.
1 分区方法
大型供水管网可有很多不同的分区方案,但大部分不能满足水力约束条件.虽然符合要求的分区布局数量有限,即使借助水力模拟软件作为辅助,仅仅通过经验或者试探方法获得合理分区方案仍然非常困难.本文提出的管网分区方法能迅速获得合理的分区.通过图论最短路径算法获得最短路径结构,在供水干管上安装水表,而在冗余管道上安装阀门,进而确定合理分区.此方法能大大降低安装阀门和水表的管道数目.
管网分区主要步骤如下:①最高时水力模拟;②根据管网结构确定邻接矩阵,根据管道流向和式(1)和式(2)确定水力路径权重矩阵和耗散路径权重矩阵;③利用Dijkstra算法计算水源到各节点的水力最短路径和耗散最短路径;④模拟结果和最短路径导入ArcGIS中,可以清晰显示压力分布最短路径管网布局,另外还可显示道路、河流等边界;⑤确定DMAs数量及区域;⑥水力路径上安装水表;⑦耗散路径上安装并关闭边界阀门,确定DMAs范围;⑧在新的管网结构基础上再次运行水力模拟;⑨计算管网性能参数;⑩评估性能参数,如不满足要求则返回⑤,重新调整分区;○1如性能参数满足要求,考虑是否有减少水表的可能性,用阀门代替水表,返回⑧;○12最终确定DMAs分区.
管网设计时一般考虑最不利情况,在最不利情况下供水能够满足要求则可认为管网在一般情况下均能够正常运行.最高时供水情形通常是管网设计时考虑的最不利情况.首先在最高用水负荷下进行管网模拟,确定管道流量、管道水头损失.然后确定管道权重.管网图的存储包括邻接表和邻接矩阵,对于稀疏图一般采用邻接表,这样比较紧凑并节省内存.对于稠密图或需迅速判断2个节点是否相连时通常采用邻接矩阵表示法.本文在最短路径计算中需要通过节点获得相应管道,因此采用邻接矩阵存储方式.为了获得供水管网干管布局和管网内部最小能量结构,本文提出了水力路径和耗散路径.
1.1 水力路径
对于已建成的供水管网,管段管径已知,单纯以各管段管长计算的最短路径往往与实际情况不符.在管长相同的情况下,管径大的管道具有更大的通水能力,为了使用图论最短路径算法,提出了水力路径概念,水力路径值越小,表示该管段在供水管网中越重要.公式如下:
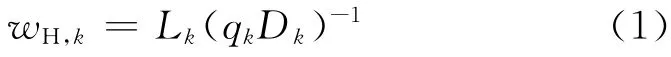
式中:wH,k为管段k的水力路径权重;Lk为管段k的管长,m;qk为管段k的流量,m3·s-1;Dk为管段k的管径,m.
在水力供水路径上的管段为供水系统中主要供水干管,充分发挥这些干管的输配水功能能最大程度降低管网水头损失,从而提高供水管网运行的经济性和可靠性.如果在这些干管上安装阀门,将破坏系统原有的主要供水路径,严重影响供水效率,产生大的能力损失.因此,在管网分区中,如需在水力供水路径管段上划分不同分区,应考虑设置水表.
1.2 耗散路径
由弹性指数[15]可知,管段内部能量耗散越小,管网弹性指数越高,可靠性越大.以管道能量损失(式(2))为权重的路径称为耗散路径.

式中:wD,k为管段k的耗散路径权重;Hk为管段k的水头损失,m.
以管段能量耗散为权重的最短路径算法得到的是从水源到节点能量损失最小的路径,如果在这种管道上设置阀门将改变水源到节点的路径,增加管网能量损失.在所有最短耗散路径中,管道经过的次数越小说明该管道越不重要,为供水管网冗余管道,因此在这种管道上安装阀门能最大程度降低阀门关闭对系统供水的影响.
在管网布局确定以后,可以方便地获得水源到节点的所有路径.设水源标记为si(i=1,…,R),节点标记为nj(j=1,…,N),管道标记为lk(k=1,…,M).其中,R,N,M分别为水源数、节点数、管道数.则水源si到节点nj的一条路径节点集合可表示为为此路径中序号为q的节点,水源si到节点nj的所有路径节点集合为为水源si到节点nj的所有路径数.对应的管道集合为在所有的路径集合{p}si,nj中,只有1 条路径为最短权重路径,则到各节点的所有最短路径为.本文使用Dijkstra算法计算最短水力路径和最短耗散路径.
水表安装在最短水力路径,由于其水头损失相对较小,对系统的影响可以忽略.而安装阀门以隔离管道将会改变水流流向,增加水头损失,因此选择阀门位置应慎重.当每个水源到各节点的最短耗散路径确定以后可以计算每个管道在所有最短路径中重复的次数fj,且不包含在最短路径中的管道fj=0.这样,原环状供水管网可变为仅包含最短路径管道的枝状网.不同类型的管道可以在ArcGIS中清晰表示,可以简化管网结构,方便规划人员选择DMAs数目和规模以及确定水表和边界阀门位置.
为了最小化安装水表和阀门对原有供水管网性能的影响应该谨慎选择相应管道.首先,根据分区供水管道相应的输配水功能,输水管道不应设置阀门和水表,以保证迅速将水量分送到配水干管.水表应该安装在DMAs配水干管入水口处,对于高压区可以设置降压阀,方便后续压力管理.确定DMAs关闭的管道越多,发挥配水功能的管道越少.在供水管网中,有一些管道是冗余的,即在最短耗散路径中管道经过次数fj很小的管道.另外,最短水力路径上的管道以及最短耗散路径上fj较大的管道均为主要配水管道,在这些管道上安装阀门将改变水流方向,增加管网能量损失,所以应避免在此类管道上安装阀门.在管网分区中遵循2个原则:①最小化关闭管道数量,尤其是最短水力路径中管道以及最短耗散路径上fj较大的管道,应加装水表而不是阀门;②尽量减少水表数量.如果可行,用阀门代替水表.
在DMAs设计时首先应根据管理和压力分布将供水管网分为几个较大的区域.然后确定DMAs数量以及规模,在最短水力路径上的配水干管上安装水表,每个节点确定所属DMAs后,在最短耗散路径上fj小的管道上(首先选择fj=0的管道)安装边界阀门,确定每个DMA 的准确边界.对完成DMAs分区后的供水管网再次进行水力模拟,评价性能参数.如性能指数不满足要求,说明管道阀门关闭导致产生很多水头损失,使得压力不足,应减少DMAs数量或调整DMAs规模,直到性能指数满足要求.随后用边界阀门代替水表,以降低成本,便于DMAs水量平衡计算.每次只取消1个水表,用边界阀门代替fj值小的管道上的水表.
2 分区评价指标
(1)能量参数:弹性指数.Todini[15]提出了供水管网弹性指数概念.供水管网总输入能量
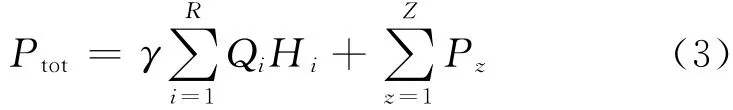
式中:γ为水的比重;Qi为水源si的供水量;Hi为水源si的水头;Pz为泵站或加压站z的输入能量,z为泵站或加压站序号,Z为泵站和加压站总数.
给水系统输入能量主要有2 种走向,一是在管网输送时通过管道水头损失而在系统内部消耗,一是通过节点出流.即
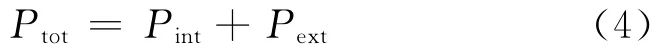
式中:Pint为内部耗散能量;Pext为输出能量.
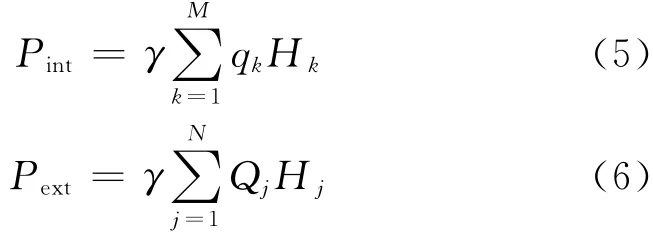
式中:Qj为节点nj的用水量;Hj为节点nj的水头.弹性指数Ir可定义为
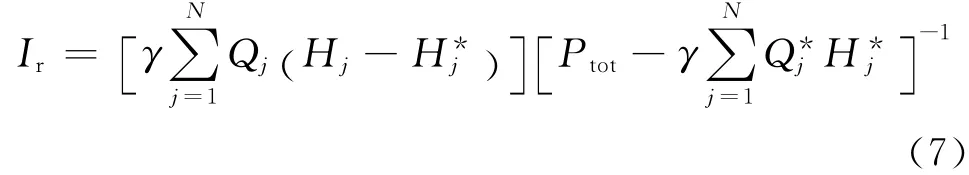
(2)统计参数:每个DMA 压力最大值、压力最小值、压力平均值.
(3)水力参数:每个DMA 内设计压力方差αd、平均富余压力、平均不足压力.
式中:d为DMA 的序号;Nd为第d个DMA 内节点数;Pdj为第d个DMA 内节点nj压力;P*为管网设计压力.对于DMA 内压力大于设计压力的节点(Pdj≥P*)平均富余压力φd为
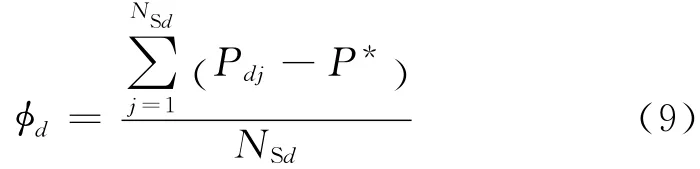
式中,NSd为第d个DMA 内富余压力节点数.对于DMA 内压力小于设计压力的节点(Pdj≤P*)平均不足压力φd为
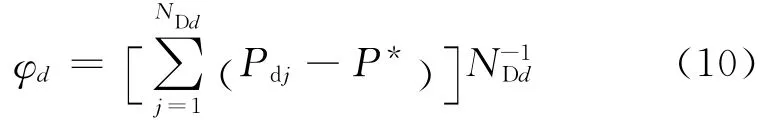
式中,NDd为第d个DMA 内不足压力节点数.
3 供水管网分区实例研究
以广州市九龙镇供水管网为例验证分区方法的有效性.该管网共有3 个水源,2 个水塔.其中水源R-1和R-2位于南部,水源R-3位于西北部,水塔T-1,T-2分别位于东部和北部地势较高处.水源R-1,R-2,R-3高程均为40m,泵站扬程均为25m;水塔高程均为60m,水位高3m.该供水管网共有326个节点、513根管段.最高时总供水量为3 448.06L·s-1.主要输水管为沿九龙大道布置的DN1200管道和R-2 向西输水的DN1000 管道,主要配水管为DN800,DN600,DN400和DN300管道.供水管段总长度为27.85km.以最高时设计流量为分区依据.因为最高时为供水管网最不利情况,此时管网最为敏感,管段的隔离对供水的影响最大.九龙镇为城乡一体化供水,根据该镇实际情况,设计压力定为24 m.管网压力分布见图1.
根据平差后的管道流量以及水头损失计算水力路径权重矩阵和耗散路径权重矩阵,然后利用Dijkstra算法计算水源到各节点的水力最短路径和耗散最短路径.图2为最短水力路径和最短耗散路径,两者的最短路径管网结构均为树状网,有助于简化分区工作,另外不同节点的分组一目了然,这有助于确定分区数量与规模.由前述可知,最短水力路径为水源到各节点的主要供水路线,因此,依据最短水力路径划分不同分区,而参考最短耗散路径图选择经过次数较少的管段为阀门管段.
基于最短路径分析,并考虑压力分布尤其是高压区和主要道路走向,将管网划分为10个DMAs分区.确定了各分区所含节点后,通过安装边界阀门和水表获得DMAs确切范围.多次模拟后确定最终的DMAs分区.各分区示意图见图3.根据行政区划将高压区分为2个分区,即DMA1和DMA3.DMA1~DMA7大致与九龙大道平行,DMA5中间节点为水源R-1和R-3供水分界线,但难以确定合适的分区,且该区域为完整的行政区域,因此确定DMA5为双向供水.中西部4个节点用水量较大且远离水源,关闭DMA3和DMA7流向这些节点的管道后其压力低于设计压力.考虑到这4个节点靠近DMA5,因此将流向该组节点的管道管径扩大为DN500管道.广河高速将R-1和R-2供水区域分为南北两侧,由此确定DMA6,DMA7和DMA8.DMA10为广汕公路南侧供水区域,剩余部分为DMA9.
表1为分区前后供水管网能量参数.未分区时弹性指数为0.652,说明该供水系统可靠性较高,原因是该供水管网布置为环状管网,3个水源从南北两侧供水,且在高处建有2个水塔,输水管道管径较大(规格为DN1000和DN1200).分区后由于管道的关闭,不可避免地降低供水管网的可靠性,因此分区后弹性指数降为0.582,但其可靠性仍然满足供水要求.另外分区前后系统输入能力有微小变化,这是由于分区改变了各水源的供水范围.表2为分区前后压力统计分析.由表可知,分区后各区域压力均有所下降.其中DMA1,DMA2和DMA8平均压力下降比较明显,因为这2个分区均靠近水源,分区后均只有1个进水口,因此压力显著下降.DMA8中最小压力小于设计压力,其原因是东部节点高程较大(为45 m),可通过建设高位水池解决低压情况.表3为分区前后水力参数,除DMA8中因部分节点高程较大导致出现不足压力外,所有分区节点压力均大于设计压力,表现为不足压力为零、富余压力大于零.另外设计压力方差反映了DMAs中压力偏离设计压力的程度,因除DMA8外所有分区不足压力为零,说明设计压力偏差为节点压力大于设计压力的程度,其数值大小可以指导下一步压力管理的优先次序,即数值较大的DMAs宜优先考虑实施压力管理降低漏损,如DMA1,DMA2和DMA3.
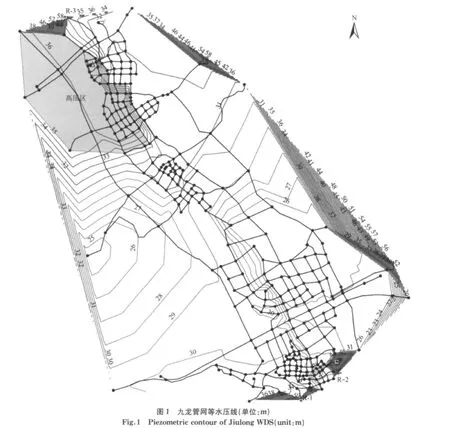
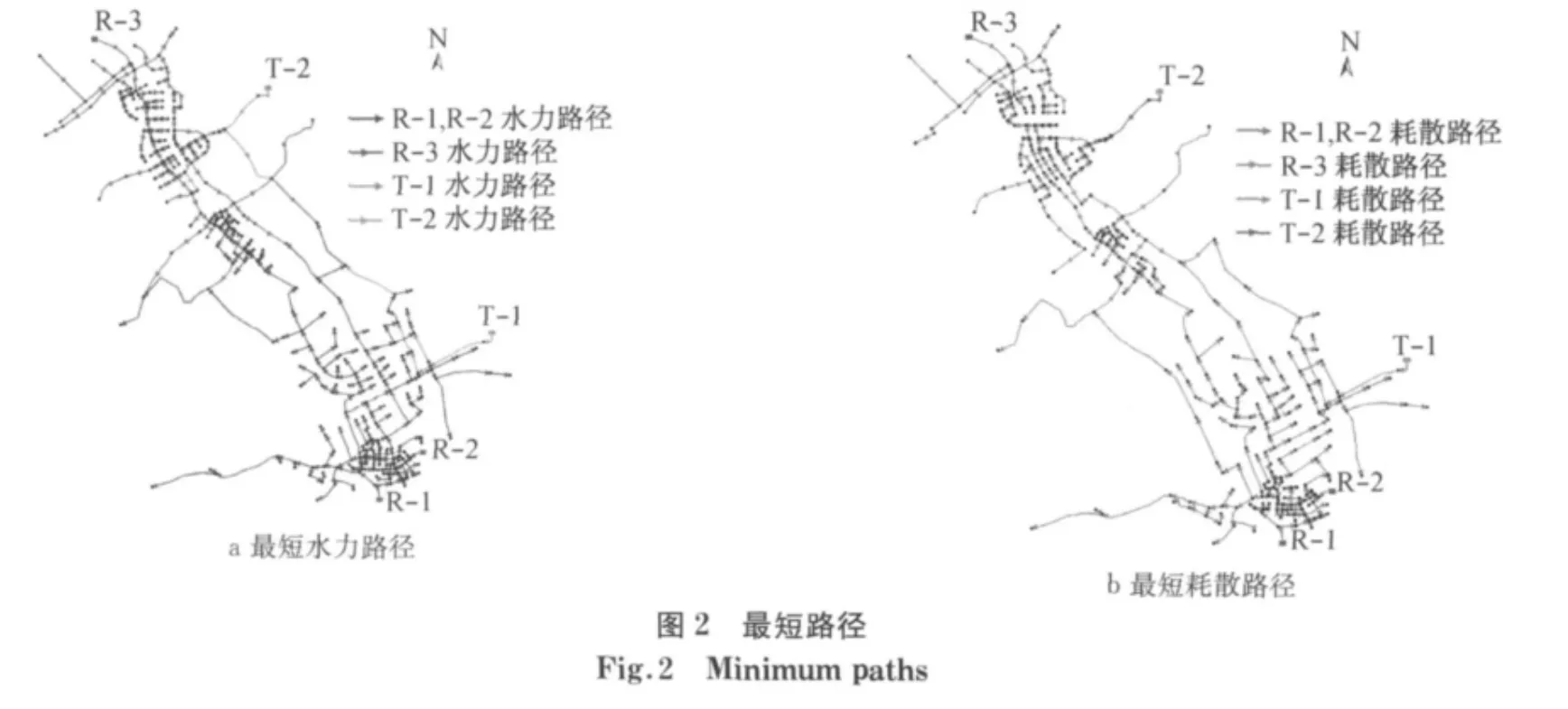
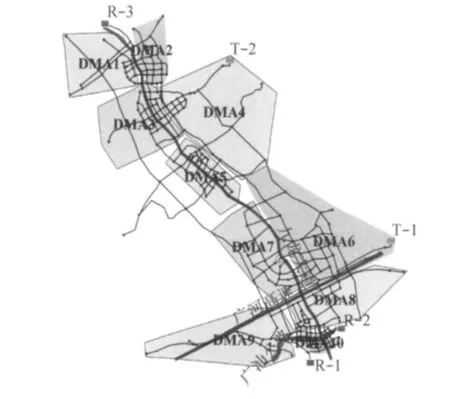
图3 管网DMAs分区示意Fig.3 Sketch map of Jiulong WDS with DMAs

表1 分区前后能量参数Tab.1 Energy indexes of Jiulong WDS
图4为分区后各DMAs的连通情况.水源R-3向DMA1~DMA5供水,水塔T-2在DMA4中,可提高其 可 靠 性.DMA3 和DMA4 由P-387 连 通.水源R-1向DMA5~DMA7,DMA10 供水,水源R-2向DMA 6,DMA 8~DMA 1 0供水,水塔T-1向DMA6供水.根据流向可以区分单向供水和双向供水,其中DMA5,DMA6,DMA10为双向供水.其他分区为单向供水,其中DMA3与DMA4直接具有管道连通,供水较安全.应该加强其他单向供水DMAs的管理,提高供水安全性.表4说明不同DMAs规模有不同的用水量,根据DMAs的入流量和出流量以及管道管件可以选择合适的水表,提高计量准确性.

表2 分区前后压力统计参数Tab.2 Statistical pressure indexes of Jiulong WDS

表3 分区前后水力参数Tab.3 Hydraulic indexes of Jiulong WDS
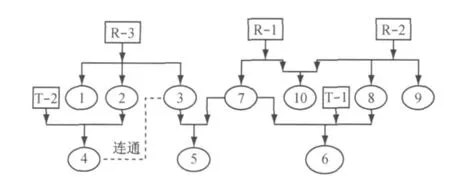
图4 DMAs连通示意Fig.4 Block Diagram of Interaction of DMAs
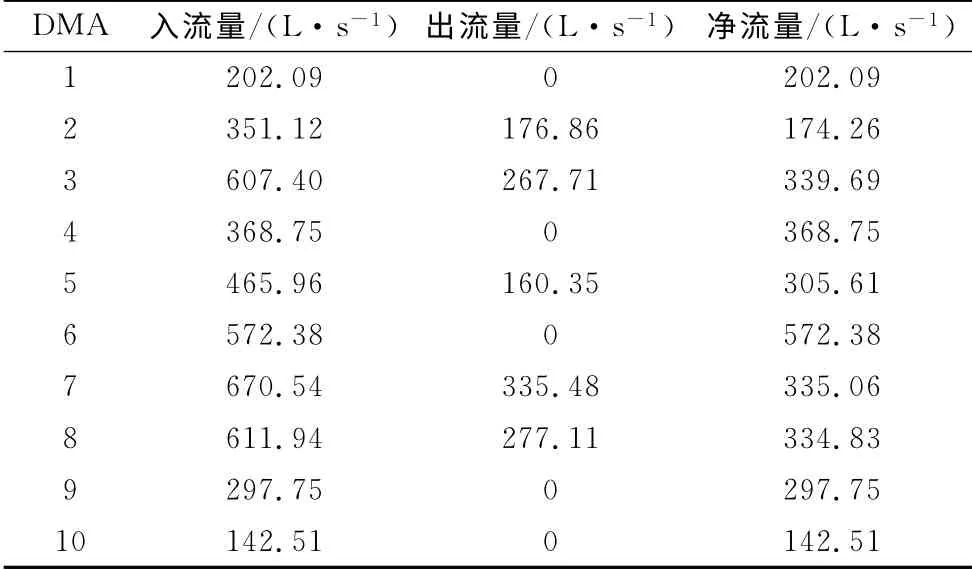
表4 DMAs流量分析Tab.4 Flow analysis of DMAs
4 结论
(1)DMAs作为新型的供水管网结构是漏损分析、日常监控的有效手段,但由于供水管网的复杂性,单纯靠人工经验难以实现合理的分区.
(2)最短路径算法结合地理信息系统可以简化供水管网结构并将其可视化,借助供水管网模拟并考虑分区影响因素,能实现满足设计要求的分区.
(3)管网分区通过安装水表和阀门来确定供水范围,水表应安装在主要供水路径上,阀门应安装在最短耗散路径经过次数较少的管道上.
(4)分区降低供水管网可靠性,因此在分区时考虑相互连通、双向供水,DMAs内设置水塔或高地水池等措施能最大程度降低分区对可靠性的影响.
(5)优先选择压力较大的DMAs进行压力管理,降低漏损.
(6)通过DMAs流入和流出流量以及安装管径可以选择合适的水表规格,提高计量精度.
[1] Hamilton S.When is a DMA not a DMA?[C]∥Proceedings of IWA Special Conference‘Water Loss 2007’.Bucharest:IWA,2007:47-56.
[2] 刘俊,孙佳,俞国平.分区供水技术在漏损控制中的研究现状与进展[J].中国给水排水,2010,26(16):7.LIU Jun,SUN Jia,YU Guoping.Current situation and progress of water distribution system zoning technologies for water loss control[J].China Water & Wastewater,2010,26(16):7.
[3] Grayman W M,Murray R,Savic D A.Effects of Redesign of Water Systems for Security and Water Quality Factors[C]∥Proceedings of World Environmental and Water Resources Congress 2009:Great Rivers.Reston:American Society of Civil Engineers,2009:504-514.
[4] Swamee P K,Sharma A K.Decomposition of a large water system and optimal zone size:design of water supply pipe networks[M].Hoboken:John Wiley &Sons Inc,2008.
[5] 黄茂林.供水管网漏损控制的DMA 技术及阀门布置的优化研究[D].长沙:湖南大学,2009.HUANG Maolin.DMA technology and optimal location of control valves in water distribution leakage control [D].Changsha:Hunan University,2009.
[6] Tzatchkov V G,Alcocer-Yamanaka V H,Ortiz.V B.Graph theory based algorithms for water distribution network sectorization projects[C]∥Proceedings of the 8th Annual water distribution systems analysis symposium.Reston:American Society of Civil Engineers,2006.1-15.
[7] Sempewo J,Pathirana A,Vairavamoorthy K.Spatial analysis tool for development of leakage control zones from the analogy of distributed computing[C]∥Proceedings of the 10th Annual Water Distribution Systems Analysis Conference.Reston:American Society of Civil Engineers,2008.676-690.
[8] Di Nardo A,Di Natale M. A heuristic design support methodology based on graph theory for district metering of water supply networks[J].Engineering Optimization,2001,43(2):193.
[9] Perelman L,Ostfeld A.Topological clustering for water distribution systems analysis[J].Environmental Modelling &Software,2011,26:969.
[10] 阎立华,刘丽英,马婷婷.图论法研究多水源管网供水分区[J].沈阳建筑大学学报:自然科学版,2007,23(1):113.YAN Lihua,LIU Liying,MA Tingting.Multi-source water supply network for subarea based on graph theory [J].Journal of Shenyang Jianzhu University :Natural Science,2007,23(1):113.
[11] 刁克功.分区管理模式给水管网的水力分析与模拟技术研究[D].北京:北京工业大学,2011.DIAO Kegong.Analysis and modeling of zonal management oriented water distribution system [D].Beijing:Beijing University of Technology,2011.
[12] Lzquierdo J,Herrera M,Montalvo I,et al.Agent-based division of water distribution systems into district metered areas[C]∥Proceedings of the 4th International Conference on Software and Data Technologies,Setubal:INSTICC Press,2009.83-90.
[13] Herrera M,Canu S,Karatzoglou A,et al.An approach to water supply clusters by semi-supervised learning[C]∥Proceedings of the 5th Biennial Conference of the International Environmental Modelling and Software Society:Modelling for Environment’s Sake.Manno:[s.n.],2010:1925-1932.
[14] Awad H,Kapelan Z,Savic D A.Optimal setting of timemodulated pressure reducing valves in water distribution networks using genetic algorithms[C]∥Integrating Water Systems.London:Taylor &Francis Group,2010:31-37.
[15] Todini E.Looped water distribution networks design using a resilience index based heuristic approach[J].Urban Water,2000(2):115.

