摆式陀螺寻北仪快速寻北的时差逆转点法

周召发，常振军，张志利

（1.西北工业大学，陕西 西安 710072；2.第二炮兵工程大学，陕西 西安 710025）

0 引言

陀螺寻北仪是近些年来兴起的常用定向仪器，其中的摆式陀螺寻北仪在航空、航天、探测、隧道、军事等领域得到广泛应用［1］。实际应用中，如导弹无依托快速发射，要求在保证精度前提下尽量缩短寻北时间，所以研究如何在较短的摆动过程中实现快速寻北具有重要应用价值。常用的寻北方法是粗寻北阶段利用磁敏感器确定大致北向方位，架设陀螺经纬仪，然后采用步进迭代法，在逆转点处改变扭力零位，逐步靠向真北；精寻北阶段采用逆转点法、时差法、中天法、积分法等，利用了摆动曲线的一些特殊点位信息寻得真北方向［2－3］。常用粗寻北过程中的磁方位法容易受到环境磁场影响，精度不高，即使与步进迭代法配合也只能达到角分量级的精度。文献［4］针对磁方位法的不足提出一种利用磁悬浮轴承检测陀螺力矩的粗寻北方法，有效缩短了寻北时间。本文提出一种新的快速寻北方法，即时差逆转点法，结合时差法和逆转点法对摆动曲线的分析。

1 摆式陀螺寻北

为了建立陀螺仪运动的动力学微分方程，求解陀螺仪转子轴的运动规律，我们首先建立如下坐标系［5］：惯性系；平动系Oξηζ；定向系（Oξ0η0ζ0）：以地球自转角速度ωe相对平动系Oξηζ转动；莱沙尔系（Oxyz）：转子坐标系。

莱沙尔系Oxyz的方位由定向系Oξ0η0ζ0二次转动达到，见图1。

图1 坐标系变换Fig.1 Relationship of coordinates

相应的变换矩阵为：

由坐标系变换关系知，莱沙尔系对平动系转动的角速度为：

由动量矩定理可得：

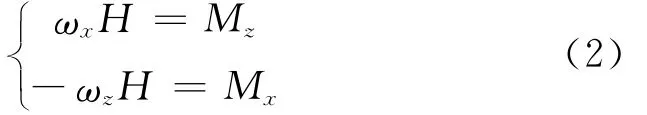
只考虑重力矩MP＝－mglsinβ的影响及式（1）代入得到运动方程：

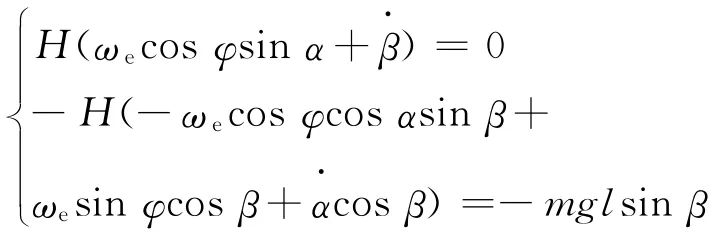
简化整理为：

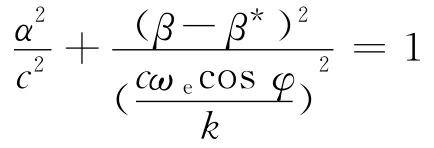
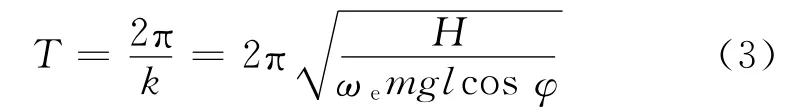
以上通过运动方程推导出周期T的计算公式，代入下文建立的时差逆转点法模型可解算出真北方向。

2 时差逆转点法

2.1 时差逆转点法原理

通过前面的分析可知，实际的摆动曲线是一个很扁的椭圆，可以认为是一条垂直于子午面作简谐振荡的直线，以时间为横轴可以得到一条正弦曲线。针对测量到的这条曲线，有很多寻北方法，本文涉及到两种：时差法由中天法演绎而来，通过测量与零刻线相对称的两刻划线在陀螺灵敏部通过的时间，求出陀螺真北方向，属于照准部固定状态下的有扭观测；逆转点法通过跟踪摆动的指标线，读取到达东西两个逆转点时度盘上读数，求出中间平衡位置，即真北方向。二者都至少需要一个周期左右的测量时间才能保证精度。

时差逆转点法结合这两种寻北方法，利用陀螺运动到一侧限位块后摆出，在出现逆转点后未出现速度最大值点及过零点就又靠到同侧限位块这个过程的角度信息，见图2，通过解算得到摆动平衡位置，具体原理如下。

1）由于限幅措施，陀螺只能在 （－αmax，αmax）的范围内摆动，α2为靠近－αmax的设定值，也可取α2＝－αmax，可得出正弦曲线的峰值：

2）由式（4）可得：

式（5）中，Δα＝α1－α2，Δt＝t2－t1。

3）则时差逆转点法计算的摆动中心为：

式（6）中，βmax为靠向限位块的读数，α1、α2分别为t1、t2时刻的摆幅值，－αmax为反向摆幅最大值，αm为初始摆幅，摆动周期T按式（3）获得。

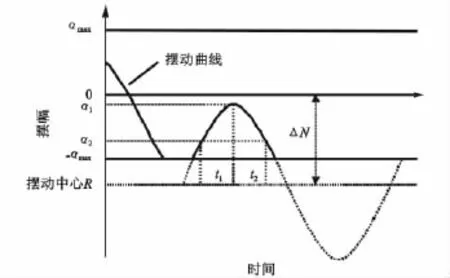
图2 时差逆转点法原理Fig.2 Theory of time difference and reversing point method

2.2 时差逆转点法步骤

具体步骤如下：

1）将地球自转速、纬度、陀螺仪参数代入周期公式（3），求得摆动周期。

2）测量逆转点及靠近限位块附近某点的时刻与摆角，利用式（5）解出振荡曲线的摆幅。

3）将测得的角度与时刻代入时差逆转点法模型即式（6），求出摆动平衡位置。

3 实验验证

粗寻北作为精寻北的铺垫，有一定的精度要求，而且在快速定向的发展趋势下，测量时间要尽可能短。时差逆转点法充分利用了半个周期以内曲线的信息量，测量上述三个点位的时刻与摆幅，结合地球自转角速度、纬度、陀螺角动量等参数解出周期，最后代入公式求出摆动中心位置。

实验过程中，为了与传统寻北方法比较精度，首先在实验室条件下预先利用方位传递确定了大致真北，即粗测真北，而后采用逆转点法和中天法精寻北，结果如表1所示，精寻北阶段测量时间约230s，精度约15″；然后直接使用时差逆转点法，得到的精度虽不如前两者高，但优于一般粗寻北方法（角分量级），且寻北时间缩短至90s，综合考虑，可以将此法作为粗寻北手段。最后利用时差逆转点法粗寻北，结合积分法精寻北，在7min内精度提高至7″。

表1 寻北测量结果Tab.1 The result of north－seeking testing

4 结论

本文提出一种摆式陀螺寻北仪快速寻北的时差逆转点法。首先计算摆动周期，然后测量逆转点及靠近限位块附近某点的摆角与时刻计算振荡曲线的摆幅，最后计算出摆动中心。实验表明：时差逆转点法更加充分地利用了摆动曲线的信息量，测量半个寻北周期内的相关点点位信息，解算出最后的摆动平衡位置，测量时间短，精度优于一般粗寻北方法，作为粗寻北手段，结合积分法等精寻北方法，能够得到更高的寻北精度。

［1］Chaumet B，Leverrier B，Rougeot C，et al.A new silicon tuning fork gyroscope for aerospace applications［C］／／Symposium Gyro Technology.2009，Karlsruhe，Germany：2009：11－12.

［2］林明春，夏桂锁，林玉池.积分法在智能陀螺寻北系统中的应用研究［J］.传感器与微系统，2007，26（10）：57－59.LIN Mingchun，XIA Guisuo，LIN Yuchi.Application of integral method in all automated intelligent gyroscope north finder［J］.Transducer and Microsystem Technologies，2007，26（10）：57－59.

［3］王缜，申功勋.摆式陀螺寻北仪的积分测量方法［J］.光学精密工程，2007，15（5）：746－752.WANG Zhen，SHEN Gongxun.Investigation on integral method of pendulous gyroscope［J］.Optics and Precision Engineering，2007，15（5）：746－752.

［4］田育民，刘思伟，白云超.摆式陀螺经纬仪粗寻北的新方法［J］.中国惯性技术学报，2009，17（4）：441－443.TIAN Yumin，LIU Siwei，BAI Yunchao.New method of rough north seeking applied in gyrotheodolite［J］.Journal of Chinese Inertial Technology，2009，17（4）：441－443.

［5］王缜，贾智东，丁扬斌，等.摆式陀螺罗盘的运动特性及其分析［J］.宇航计测技术，2006，26（4）：13－14.WANG Zhen，JIA Zhidong，DING Yangbin，et al.The motion analysis of gyrocompass［J］.Journal of Astronautic Metrology and Measurement，2006，26（4）：13－14.