考虑多径衰落的卷积编码参数确定方法

夏 彬，余孝安，成红涛，张 珂

（西安机电信息技术研究所，陕西 西安 710065）

0 引言

目前常规兵器遥测系统传输的是模拟信号或数字信号，而且不存在上行链路，对于误码率的要求仅限于10－4～10－5，通常对被传输信号进行放大／压缩、编码、调制、解调四步处理，就能实现正确的传输。

随着常规兵器的制导化发展，愈来愈多的常规武器系统呈现出多方式制导控制的趋势，使得无线传输信号种类也日趋复杂，除了传输大量的模拟、数字信号外，对数字图像信号的远距离传输也提出了要求，这就对遥测传输信道的质量（误码率）提出了更高的要求。不仅如此，战场无线传输信道的电磁环境日趋复杂，无线传输距离也在不断增加，无线信号载体的运动速率也在不停地加快，随之也会带来系统误码率过高的问题，从而无法达到可靠的传输要求。于是，在遥测系统设计中，越来越多地采用了信道编解码技术，以降低系统误码率，提高系统的可靠性。

卷积码是一种重要的抗干扰码，是一种在译码时能够自动纠错的码字。它是将k个码元划分为一段，再按一定规则产生r个校验元，最终输出n＝k＋r的一个码组，每个码组编出的校验元不仅与本组码元有关，而且与前m组的码元有关，表示为（n，k，m）。由于充分利用了码组之间的相关性，纠错能力强，所以常规兵器遥测系统中的信道编码器常常选用卷积码来进行编码。而卷积码参数的确定却一直是根据经验来进行选择，从未经过分析计算，量化得到，经常会造成系统设计余量过大，资源浪费的问题。不仅如此，现在公开发表的文献中，大多数文章往往只强调了卷积编码器的设计，而未对卷积码参数选择问题进行描述。少数文章在进行卷积码参数选择时，是按照接收端对码字的正确译码概率经验公式，将系统要求的误码率值代入公式，来估算参数值的，但是这种方法在公式的获得及应用过程中，并没有对实际传输系统的信道环境进行分析，也没有清楚地描述该公式适用的信道环境，只是进行了简单的代入求值应用，所以其准确性值得商榷，应用范围也是十分局限的。针对此问题，本文提出了考虑多径衰落的卷积编码参数确定方法。

1 传统常规兵器遥测系统卷积编码参数确定与信道计算

1.1 传统常规兵器遥测系统卷积编码参数确定方法

信道编码的基本思想是：通过对发送端信息序列作某种变换，使原来彼此独立，相关性较小的信息码元产生某种相关性，在接收端利用这种相关性来检查并纠正信息码元在信道传输中所发生的差错［1］。

信道编码的一般方法是：在待传输的信息序列中，通过一定的算法，人为地加入一些多余的码元，在接收端再按此规律对收到的码字进行检查，从而发现或者纠正传输过程中的错误。但新加入的码元不含任何有效信息，这样必然使信息率下降，增加传输带宽，即可靠性的提高是通过降低有效性来实现的［2］。

在 （n，k，m）卷积码中，参数n越大，可靠性会越高，但是有效性会降低，参数m越大，相关性会越高，可靠性也会越高，但是译码器的复杂程度也会成指数上升。所以针对可靠性和有效性的矛盾，如何构造出以最小冗余度代价换取最大抗干扰性能的“好码”就成为遥测系统设计的关键。

目前常规兵器遥测系统在确定卷积码参数的方法上并没有统一的分析计算方法，在进行信道编码器设计时，往往按照其它系统（未出现过失效的遥测系统）中卷积码的参数来进行设定，这样常常会造成在信道环境相对比较规则、地势开阔、强散射体密度低时，而依然选择了较大的n或m，使遥测系统的有效性未能达到最优，译码器的设计也更加复杂。反之，如果所处信道环境复杂，也会因为选择的n或m不够大，而达不到系统的可靠性要求。

1.2 信道电波损耗、多径衰落计算

常规兵器遥测系统采用S波段电波作为信号载体，属视距传播方式。常用投弹高度为6km，所以电波的传播途径主要部分在对流层中。此时，电波传播路径损耗Lf主要包括自由空间中电波损耗Lof和极化损耗Lif。电波损耗Lof可由式（1）计算：

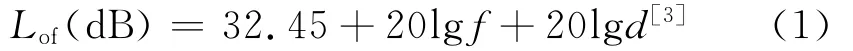
式中，f为载波频率（MHz）；d为传输距离（km）。

但是，在实际无线传输过程中，除了大气对传播进行影响外，其它如地形地貌也会对传输效果产生较大影响。例如树林、山丘以及建筑物会阻挡无线信号的传输并造成损耗；光滑的水面以及平坦的地面也会造成微波反射，反射波经叠加后可能会造成信号的衰减。在地面无明显障碍物时，反射也是影响无线传输质量的主要因素。常规兵器遥测属于低仰角条件下的数据传输链路，因此还需要对地－空链路中的多径效应衰落进行分析。

在电波的传输过程中，波阵面上的每一点都是一个进行二次辐射的球面波的波源，即二次波源。而空间任一点的辐射场都是由包围波面的任意封闭曲面上各点的二次波源发出的波在该点相互干涉、叠加的结果。封闭曲面上各点的二次波源到达接收点的远近不同，这就使得接收点的信号场强的大小发生变化，这也是产生多径效应的根本。

由多径引起的干涉型衰落，是由直射波和反射波在到达接收端时的行程差导致它们的相位不一致，而在叠加时产生的电波衰落。由于这种衰落与行程差ΔR有关，而ΔR是随大气的折射参数K值的变化而变化的。这种衰落在水面、湖泊和平滑的地面时显得特别严重。信号传输模型如图1所示。

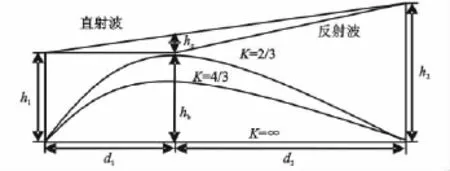
图1 低仰角传输链路模型Fig.1 The transmission link model of low elevation

图1中，h1为地面接收天线高度，h2为弹载天线高度，hc为菲涅尔余隙，hb为等效地球凸起高度，K为等效地球半径因子，标准大气折射条件下取4／3，d1为地面接收站至反射点距离，d2为飞行器至反射点距离。若传输系统要求电波的传输路径为视距，对于K＝Kmin、K＝4／3、K＝∞ 几种情况均应能满足余隙标准，即当K＝Kmin时，传输余隙最小，此时要保证电波的绕射损耗不会对通信系统带来较大的影响；但当K＝∞时，传输余隙最大，电波的反射情况最严重，此时就必须要考虑信号衰落对通信系统的影响。

假设多径衰落损耗为Fd，则Pe系统误码率与Fd关系的经验公式可以表达为式（2）：

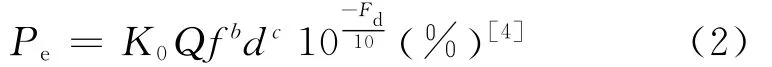
式中，

系统的实际增益值可由式（4）计算出。

式中，KR为接收增益；KT为发射增益；GT为发射天线增益；GR接收天线增益（含低噪放）。

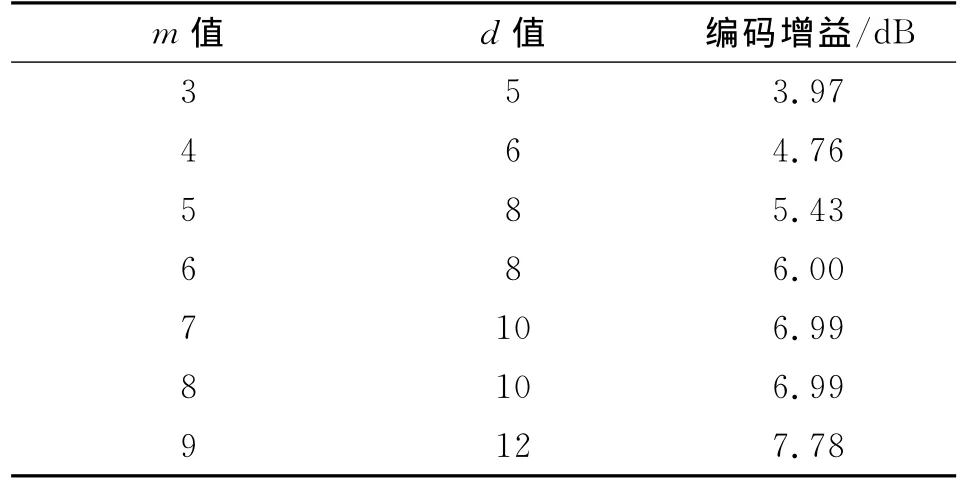
表1 R＝1／2卷积码编码增益［5］Tab.1 The convolution coding gain at R ＝1／2

通过对信道电波损耗、多径衰落的分析就可以计算出信道的损耗值，这个计算值与系统实际增益值的差就可以确定编码的实际最小增益值，再根据表1就能够确定卷积编码的参数了，这种方法确定的卷积码参数将更加准确。

2 考虑多径衰落的卷积编码参数确定方法

这种考虑多径衰落的卷积编码参数确定方法步骤框图如图2所示。首先由自由空间中电波损耗、极化损耗以及多径衰落损耗计算自由空间电波传播路径损耗；然后根据通讯距离方程计算系统实际增益值；接着由电波传输路径损耗与系统实际增益值算出信道编码增益的最小值；最后由计算出的编码增益，考虑设计余量后查表确定信道卷积编码的参数值。

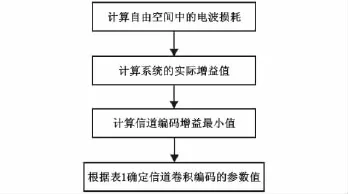
图2 考虑多径衰落的卷积编码参数确定步骤框图Fig.2 The flow chart of convolution code definition based on muti－path fading

2.1 计算电波传播路径损耗

经过前述信道分析，电波传播路径损耗Lf主要包括三部分损耗值：自由空间中电波损耗Lof、极化损耗Lif以及多径衰落损耗Fd。

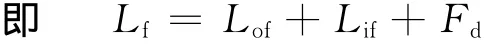
电波损耗Lof可由式（1）计算，代入实际f为载波频率（MHz）、d为传输距离（km）即可。

极化损耗Lif是由于弹载发射天线与接收天线的极化方式不同造成的损耗，在常规兵器遥测的信道中该损耗值通常取3dB。

多径衰落损耗的计算则较为复杂，对于常规兵器遥测信道的近似计算，一般要求菲涅尔余隙hc≥0.6F1，此时电波的传输路径可视为视距。根据系统误码率Pe与多径衰落损耗Fd关系的经验公式（2）来完成多径衰落损耗计算。

其中K0为气候条件因子，对于水面及衰落严重的地形K0＝3.25×10－3；b为频率因子，b＝1.3；c为距离因子，c＝3.1；f 为载波频率（MHz）；d 为传输距离（km）。由式（3）先计算出Q 值，再根据式（2）即可计算出传输信道的多径衰落损耗Fd。

2.2 计算系统的实际增益值

根据通信距离方程式（4）代入系统各项参数后，即可计算出系统实际增益值L′f。

2.3 计算信道编码增益最小值

将电波传输路径损耗Lf与系统实际增益值L′f进行差运算，二者的差值即为信道编码增益的最小值。通常，我们把在给定误码率下，编码与非编码传输相比节省的信噪比Eb／N0称为编码增益。所以编码后所增加的编码增益的值，就相当于编码后提高系统传输信噪比的值。

2.4 确定信道卷积编码的参数值

根据信道编码定理可知：误码率Pe是随着约束长度m或码长n的增加而呈指数下降的，但是码长n越大，编码效率R＝k／n将降低，信道带宽或码速率也将增加（n－k）／k倍，编译码设备也越复杂。所以n和k的值应结合实际传输系统特点进行选择，当遥测信道环境相对规则，地势开阔时，一般设定（n－k）／k＝1，即编码效率R＝1／2，则取n＝2，k＝1。当遥测信道环境非常复杂时，可根据复杂程度将n值增加。

当R＝1／2时，约束长度为m时具有最大自由距离的好码与对应的编码增益上界，如表1所示。由表1可看出，直接加长卷积码的约束长度m，可以提高编码增益，每增加一位约束长度可获得约0.5dB的编码增益。根据计算出的编码增益，考虑设计余量后，在表1中选出大于计算出的编码增益值所对应的m和d的值即为该系统所需卷积码m和d的值。

3 信道编码系统模型仿真

按照某常规兵器遥测系统参数（f为2 250.5 MHz，d为200km，极化损耗为3dB），根据式（1）计算出该系统电波传播路径损耗为148.52dB，再按照系统误码率Pe要求为10－5，根据式（2）计算出多径衰落损耗Fd为57.9dB，再由式（4）计算出系统实际增益值为201.8dB，最后根据损耗值与系统增益值的差即可计算出该遥测系统最小编码增益为4.62 dB，考虑设计余量后，根据表1确定该遥测系统信道编码码型为（2，1，5）卷积码。

为了确定所选（2，1，5）卷积码是否能够带给该遥测系统大于4.62dB的编码增益，建立了如图3的系统模型，通过Matlab仿真，进行分析。该仿真系统参数及工作过程完全模拟实际遥测系统参数及工作过程。

图3 仿真系统模型框图Fig.3 The model diagram for system simution

该遥测系统主要配挂飞机，试验通常选择在人烟稀少的沙漠戈壁上，信道环境相对比较规则，地势开阔，但由于是远距离传输，存在多径衰落及电波损耗，所以图3中的模拟信道采用多径瑞利衰落信道。调制方式采用该遥测系统实际应用的FM方式。

图3中的信号源是由Matlab的随机函数产生的二进制码序列，该码序列作为模拟遥测基带信号，经过（2，1，5）卷积编码后，以调频方式调制，进入模拟信道，经信道衰减后的信号再通过FM解调、Viterbi译码，从而还原出二进制码序列，将此码序列与原码序列进行对比，误码个数与码字总数之比即为误码率Pe。

在仿真过程中，先固定模拟信道噪声功率，然后改变发送信号功率，来获得一系列信噪比值。此处用信噪比值的变化来反应系统增益的变化。发送信号功率从－10dB开始，每2dB一个间隔取值，经过图3的仿真系统后，通过对译码后数据与信号源数据比较，计算出相对应的系统误码率，描点画图得到二者的关系曲线，如图4中“○”号曲线所示。

为了与未加（2，1，5）卷积编码的传输系统误码率性能进行比较，将图3所示的仿真系统模型中的卷积编码与Viterbi译码部分删去，直接将二进制码流经调频调制后送入多径瑞利衰落信道，接收解调后，计算误码率。在仿真过程中，同样固定噪声功率，而改变发送信号功率，完成不同信噪比取值，经过删去信道编解码的仿真系统后，计算相对应的系统误码率，描点绘出二者关系曲线，如图4中“＊”号曲线所示。

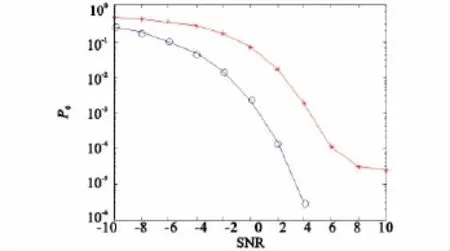
图4 误码率性能曲线Fig.4 The characteristic curve of BER

由图4可看出，“○”号曲线中，随着系统信噪比的提高，系统的误码率急剧下降。“＊”号曲线中，随着系统信噪比的提高，系统的误码率下降较慢。也就是说在相同的信噪比下，加了信道编解码传输系统的误码率均低于未加信道编解码传输系统的误码率，而且可以看出，在信噪比较差时，添加信道编解码提升的误码率性能并不明显，随着系统信噪比的提升，添加信道编解码提升的误码率性能也愈加明显。充分说明，在传输系统中，如果需要通过信道编解码来有效提升系统误码率性能，那么该传输系统应当具备较好的信噪比。也就是说系统信噪比的优化对系统误码率性能的提升至关重要。

由于实际遥测系统的误码率Pe要求为10－5，从图4中可看出，当误码率为10－5时，添加（2，1，5）卷积编码的传输系统所要求的信噪比仅为3，而未添加（2，1，5）卷积编码的传输系统所要求的信噪比已经超过8，也就是说误码率Pe要达到10－5，在不添加（2，1，5）卷积编码的条件下，系统的发射功率要增加5dB以上。反过来也就是说，添加了（2，1，5）卷积编码的系统比未加编码的系统，增加了5dB以上的编码增益，编码增益大于4.62dB，满足了此前系统的最低编码增益要求，从而进一步说明，用该方法确定的卷积码的参数能够准确有效地提供系统所需的编码增益。

4 结论

本文提出了一种考虑多径衰落的卷积编码参数的确定方法。该方法首先由自由空间中电波损耗、极化损耗以及多径衰落损耗计算自由空间电波传播路径损耗；然后根据通讯距离方程计算系统实际增益值；接着由电波传输路径损耗与系统实际增益值算出信道编码增益的最小值；最后由计算出的编码增益，考虑设计余量后查表确定信道卷积编码的参数值。仿真结果表明：该方法确定的卷积码的参数能够准确有效地提供常规兵器遥测系统所需的编码增益，从而避免了盲目选择参数时造成的系统资源浪费和系统有效性的降低。

［1］王新梅，肖国镇.纠错码——原理与方法［M］.修订版.西安：西安电子科技大学出版社，2001.

［2］王育民，李辉，梁传甲.信息论与编码理论［M］.北京：高等教育出版社，2005.

［3］樊昌信.通信原理［M］.第四版.北京：国防工业出版社，1995.

［4］《通信工程新技术实用手册》编委会.通信工程新技术实用手册——数字数据通信技术分册［M］.北京：北京邮电大学出版社，2002.

［5］吴沫，杨华，卢伟.几种信道编码方式的编码增益比较分析［J］.通信技术，2007，40（11）：220－225.WU Mo，YANG Hua，LU Wei.Research on coding gain of channel coding［J］.Communications Technology，2007，40（11）：220－225.