基于HHT算法的轨道信号解调研究

杨菲菲，杜普选

（北京交通大学 国家电工电子教学基地， 北京 100044）

目前，轨道信号主要使用FFT（Fast Fourier Transform）和ZFFT（Zoom-FFT）结合的方法得到信号的调制频率、上下边频，这些方法不能同时从时域和频域2方面对信号进行分析，信号的上下边频不能从频谱图上直接观察到。为此，本文采用一种新的时间序列信号分析方法解调轨道信号，即希尔伯特-黄变换（Hilbert-Huang Transform，HHT）算法。

1 ZPW2000轨道信号模型

ZPW2000轨道信号的低频和载频采用频偏为11 Hz的UM71技术。该信号的频谱特征是载频附近的能量最大，上下边频附近的能量次之。信号载频有4种并且每种又分为1型和2型，4种载频分别为上行2 000 Hz、2 600 Hz，下行1 700 Hz、2 300 Hz。低频调制信号共18种，以1.1 Hz的频率从10.3 Hz～29 Hz递增[1]。

采用相位连续的FSK信号的ZPW2000轨道信号，其时域表达式为[2～4]：

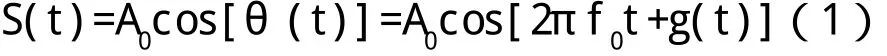
其中：

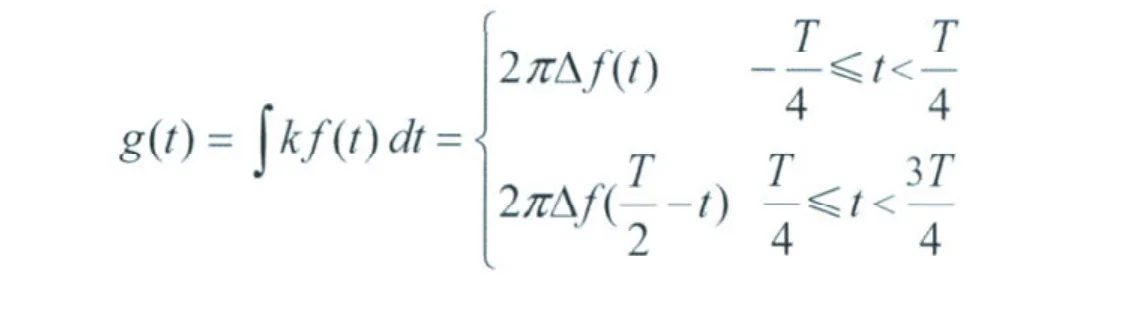
轨道信号的解调就是通过某种算法得到该键控移频信号的载频f0，调制频率f1=1/T，上边频Fh=f0+△f，下边频Fl=f0－△f。

2 HHT原理

HHT由经典模态分解（Empirical Mode Decompo-sition，简称EMD）和Hilbert谱分析构成。HHT算法就是用EMD方法按照信号含有的信息量的不同，逐级分解成一系列的本征模态函数（Intrinsic Mode Function，IMF），然后求得每个IMF分量的解析函数，由解析函数求得其瞬时频率和振幅[5]。

在HHT算法中，瞬时频率的表达式为：

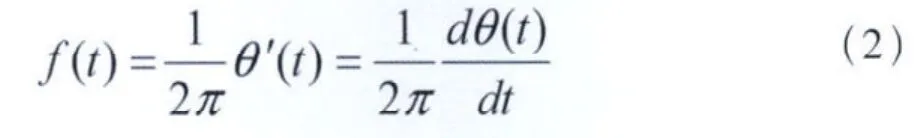
EMD通过自动调节时间尺度得到满足要求的IMF函数。IMF函数满足的性质为：（1）函数中所有的过零点的个数和极值点的个数之差的绝对值≤1；（2）在整个序列中，分别由信号的局部极大值和局部极小值形成的上下包络的平均值处处为零或几近于零。

EMD的筛选过程如下：首先分别求出原始信号y(t)的极大值和极小值点的上下包络线，用y(t)减去上下包络线的均值得到第一个残余函数，如果该残余函数满足IMF函数的条件，则记为第一个IMF分量c1(t)。如果不满足条件，则把该残余函数视为一个新的信号重复上面的操作，直到找到符合IMF函数条件的残余函数，把这个残余函数记为第一个IMF分量，然后用y(t)减去c1(t)得到一个新的信号，重复上面的操作，得到其他IMF分量。分解停止的条件是直到找到的残余函数是一个单纯的递增或递减函数。得到EMD的最后分解式为[6]：

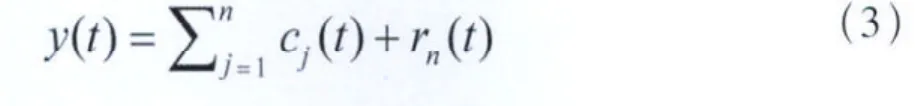
其中rn(t)为残余函数，cj(t)为IMF分量。

3 用HHT算法对ZPW2000轨道信号解调

不同于以往用EMD分解和FFT算法结合的方法解调轨道信号，本文通过EMD分解得到正交的IMF分量，同时应用其瞬时频率较为精确地解调出轨道信号的有用信息。

在实际环境中，铁路信号不是纯粹的FSK信号，所以在对信号的分析中加入了频率为1 950 Hz和2 050 Hz的正弦噪声。本文以载频2 000 Hz、调制频率22.4 Hz、频偏11 Hz、信噪比为5 dB的轨道信号为代表进行分析。具体分析步骤如下：

（1）采用频域滤波法对加入的正弦噪声信号进行滤波。

（2）信号的EMD分解。求出滤波后的信号y1(t)的所有极值点（极大值点和极小值点），用3次样条插值法进行曲线拟合，构造信号的上下包络，求出两者的均值m0(t)。用信号y1(t)减去m0(t)均值得到h1(t)，判断h1(t)是否满足IMF的2个性质，如果不满足，则把h1(t)视为新的信号，重复上面的操作，直到找到满足IMF条件的信号hk(t)，令c1(t)=hk(t)，得到第一个IMF分量，和残余信号r1(t)=y1(t)－c1(t)。对残余信号继续进行EMD分解，直到残余分量为常量或者是单调函数。这样就得到了全部的IMF分量。

（3）求IMF分量的解析函数，并得到其瞬时频率（简称IF）。

（4）求出上下边频和载频。由瞬时频率图可以看出上下边频以某个值上下波动，为了求出准确的值，对瞬时频率做一些数据上的处理。首先求出瞬时频率IF在规定的时间窗口上的平均值f，以均值f作为中心把IF分为2个部分，即所有大于f的频率为一部分，所有小于f的频率为另一部分；对这2部分分别设置一个合适的范围，求出该范围以内的所有数据的平均值，所得的均值就是上边频fh和下边频fl；载频f0=(fh+fl)/2。

（5）求调制频率。由于从瞬时频率图形中不能直接求出调制频率，所以本文对瞬时频率做归一化处理。即对频率大于均值f的频率置为1，对频率小于均值f的频率置为0，从而构成了一个方波信号。找到该方波中每个上升沿对应的位置，记为ki(i=1,2,…），则调制频率为1/[(ki－ki－1)●△t]，使用8 192 Hz的采样频率，所以采样周期△t为1/8 192 s，为得到精确的结果，对得到的所有调制频率求平均值，得出最后的调制频率。

4 Matlab仿真结果分析

载频为2 000 Hz、调制频率为22.4 Hz、频偏为11 Hz、 信噪比为5 dB的轨道信号，经EMD分解得到10个IMF分量，如图1。可知当分解到第10个IMF分量时，分量值基本接近于0，所以分解完毕。

图1 EMD算法分解出的IMF分量

为了简化计算量，有些IMF分量所含的信息量很少可以舍去。本文通过对IMF分量的频谱与原始信号的频谱作对比，找到和原始信号频谱几乎相同的IMF频谱，如图2。图2中（1）、（2）、（3）分别是第1个IMF分量的频谱、第2个IMF分量的频谱、原始信号的频谱。通过图可知第1个IMF分量几乎和原始信号相同，这样只需取第1个IMF分量作为研究对象即可，可以减少运算量，加快解调的速度。

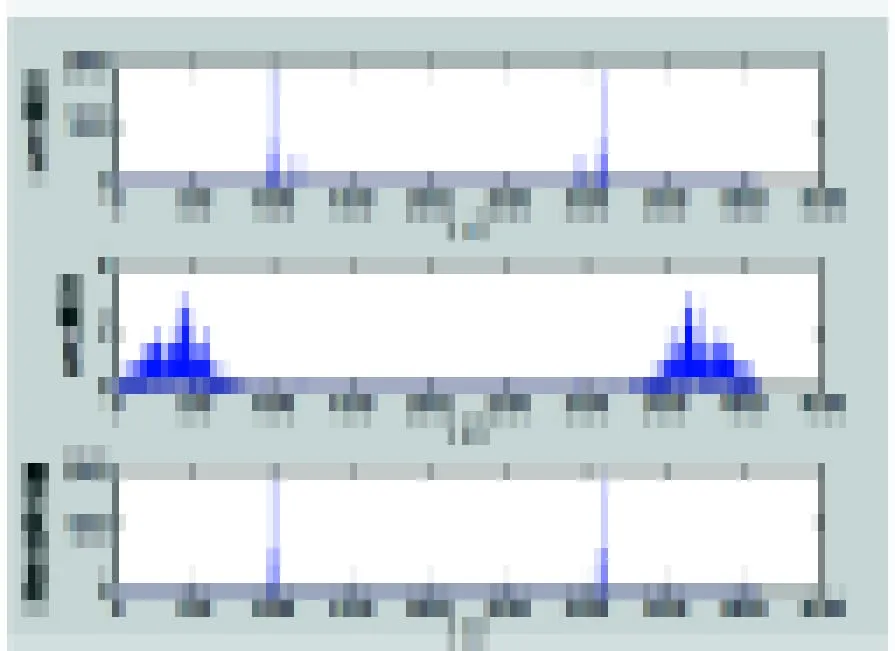
图2 前2个IMF分量的频谱与原始信号的频谱对比图

求得的第1个IMF分量的频谱，如图3，由图可知，该信号的中心频率在2 000 Hz，上边频以2 011 Hz为中心震动，下边频以1 989 Hz为中心震动。采用上述介绍方法可求出实际的上边频为2 010.948 4 Hz，下边频为1 988.852 1 Hz，中心载频为1 999.867 1 Hz。误差在0.15 Hz以内，达到轨道信号解调精度的要求。为了得到精确的调制频率，采用归一化处理，并对信号多个周期的调制频率求平均值，如图4。最后得到的调制频率为22.400 9 Hz，误差为0.000 9 Hz，解调结果非常理想。

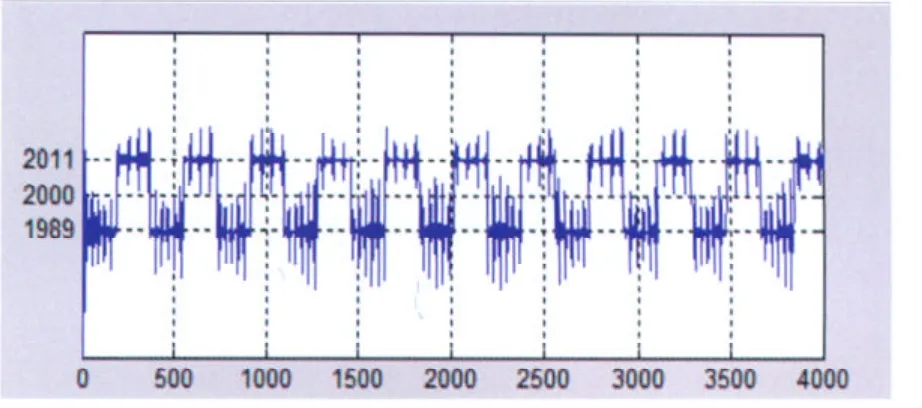
图3 第1个IMF分量的瞬时频率

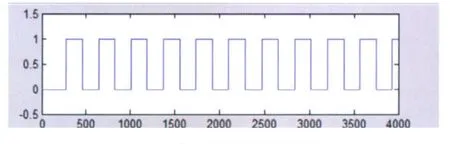
图4 第1个IMF瞬时频率归一化

通过对ZPW2000轨道信号其他载频的解调仿真，得到的解调结果和载频为2 000Hz的解调结果具有相似的精度，调制频率的解调结果比以往的解调精度高出很多，可见用HHT算法解调轨道信号是行之有效的。

5 结束语

本文采用HHT算法解调轨道信号，用HHT算法的核心经典模态分解法（EMD）得到本征模态函数（IMF），并求得瞬时频率，通过瞬时频率并结合信号的归一化处理，实现了在信噪比较低的情况下对轨道信号的精确解调。与已有算法比较，本算法简单，解调精确，可以直观地得到信号的上下边频。

[1]林瑜筠，李 鹏. 铁路信号新技术概论[M]. 北京：中国铁道出版社，2007.

[2]柳艳红，马瑞军，魏学业. EMD算法在移频信号解调中的应用研究[J]. 电子测量与仪器学报，2006，20（5）：34-38.

[3]周明晰，卢 迪，刘晓辉. 基于EMD和ZFFT的UM71轨道信号解调算法研究[J]. 自动化技术与应用，2008，27（9）.

[4]王雪丽. 基于TMS320C6720的轨道信号解调方案研究[J].北京交通大学，2010.

[5]N.E.huang, Z.Shen, S.R.Long, etai. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proc.R.Soc.Lond.A, l998.