遗传算法在树枝型专用线取送车作业中的应用研究
潘东亮
(神华包神铁路有限责任公司 科技信息部,包头 014014)
专用线取送车作业是铁路货运站的一项重要工作内容。合理地安排取送车顺序,有利于加速车辆的周转,缩短车辆的非生产停留时间,从而有效地提高铁路货物运输的效率。对于求解树枝型专用线取送车优化问题,提出了很多方法,也取得了一定的成果,其中遗传算法的贡献尤为显著。遗传算法(Genetic Algorithm-GA)是借鉴生物界自然选择和自然遗传机制的随机搜索算法。遗传算法作为一种搜索算法有着无可比拟的优点,表现在鲁棒性强、全局搜索、并行性和高效性。
(1)文献[1]和文献[2]将取送车作业问题转化成旅行商问题,以调车机车行走时间最短为优化目标,采用固定的交叉概率和变异概率,降低了搜索到问题最优解的效率;
(2)文献[3]和文献[4]利用哈密尔顿图求解树枝型专用线取送问题,该方法简单直观,但是当问题的规模较大时,却难以找到最优解;
(3)文献[5]以调车机车在整个取送作业中总耗时最少为最优目标,提高了铁路货物运输的效率,但是只求得了送车顺序,没有求得取车顺序,当以调车机车在整个取送车作业中总耗时最少为最优目标时,取车顺序不是简单地由送车顺序决定的,取车顺序与装卸车时间有很大的关系。
上述文献都将取车作业和送车作业分离开,没有把它们看成是一个完整的作业,这样不利于合理地安排取送车计划。结合以上文献的成果,对树枝型专用线取送车问题进行了更深一步的研究,将取送车作业看成是一个完整的作业,不但得到送车顺序,而且得到取车顺序,同时建立了以调车机车在整个取送车作业中总耗时最少为最优目标的数学模型。采用改进的遗传算法求解该问题,能够得到合理的取送车顺序,从而得到问题的最优解或近似最优解。
1 树枝型专用线取送车问题的描述
1.1 树枝型专用线取送车的特点
树枝型专用线取送车作业的特点是:调车机车向某一专用线送取车完成之后不必返回车站,就能去其他专用线送取车,各专用线车辆的入线时刻不同,取回站内的时刻相同。本文讨论的树枝型专用线如图1。
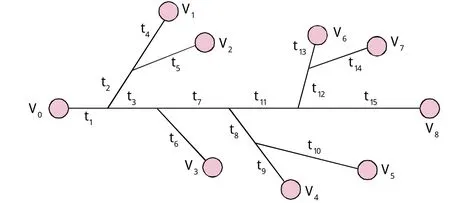
图1 树枝型专用线布置示意图
图1中V0代表调车机车的出发点和终点,Vi(i=1, 2,……, 8)代表各专用线的作业地点,ti(i=1, 2, ……, 15)代表调车机车在各路段的行走时间,这是已知的条件。由于现实中的取送车作业还受人为、天气等众多因素所影响,为了便于问题的讨论,还需做如下假设:
(1)送往各专用线车辆的作业时间是已知的,其他辅助作业时间忽略不计;(2)有且仅有一辆调车机车负责一次取送车作业。
1.2 树枝型专用线取送车数学模型
数学模型建立的好坏直接影响到是否能正确地搜索到问题的最优解。本文追求的最优目标是调车机车在一次作业中耗时最少,将取送作业看成是一次完整的作业,所以调车机车在一次作业中的耗时由送取车时间和等待完成作业时间决定,由此得到树枝型专用线取送车数学模型:

其中,tij代表调车机车从专用线i到专用线j的行走时间(i=0, 1, 2,……, n;j=0,1, 2,……, n;n代表专用线),由于调车机车从站内出发,最后回到站内,所以一共有2n+1项tij,这样就能保证把送往各专用线的车辆都能取回;tn'代表等待作业完成时间。设tn代表调车机车第2次到达专用线n与第1次到达专用线n的时间差,tn''代表调车机车第2次到达专用线n用的时间,tn'代表调车机车第1次到达专用线n用的时间,Tn代表专用线n的作业时间,则有如下关系:

如果Tn>tn,则调车机车取回专用线n的车辆时,等待作业完成时间公式如下:

如果Tn 用(0,a1, a2,……, an-1,an, a1, a2,……, an-1, an,0)表示一条染色体,基因ai(i=1, 2, ……, n)为[1, n]之间互不重复的自然数,代表专用线。例如:染色体(0, 1, 2, 3, 2, 3, 1, 0),第1个0代表调车机车从站内出发开始作业,第2个0代表调车机车完成作业回到站内;第1个1代表调车机车将车辆送到专用线1,第2个1代表调车机车将车辆从专用线1取回,那么这条染色体的送车顺序就是1、2、3,取车顺序是2、3、1。 由于遗传算法的初始种群随机产生,优良染色体较少,极大地降低了算法的搜索效率。为提高算法的搜索效率,算法按照以下步骤生成染色体。 (1)送车时将作业量大的专用线尽量排在前面,作业量小的专用线排在后面;取车时将作业量小的专用线尽量排在前面,作业量大的专用线排在后面,减少调车机车的等待时间。 (2)设种群规模为M,则产生2 M个染色体,计算每条染色体的适应度,按照适应度大小将2 M个染色体进行排序,保留前M个染色体作为初始种群,淘汰后M个染色体。 在遗传算法中,用适应度来确定某个体能进行遗传操作的概率。适应度较大的个体遗传到下一代的概率大,而适应度较小的个体遗传到下一代的概率就小。度量个体适应度的函数称为适应度函数。本文求解的最优目标是调车机车在一次作业中耗时最少,所以适应度函数f(x)为: 2.3.1 选择运算 选择运算采用精英比例选择。记忆当前最优的个体,用它来替换本代群体经过交叉、变异后适应度最低的个体,对其他群体进行比例选择运算。这种选择运算的优势是个体适应度大小与个体被选择的概率成正比,利于种群的优化,能保证搜索到问题的最优解。 2.3.2 交叉运算 交叉运算采用两点交叉。在(1,染色体长度-2)之间随机产生两个交叉点,交换待交叉两条染色体两个交叉点之间的基因,得到两条新的染色体。判断新的染色体是否合法,如果合法进入后续的运算;不合法将两条新的染色体调整成合法的染色体,进入后续的运算。本文采用自适应的交叉概率。设f为某条染色体的适应度,favg为种群的平均适应度,随机产生(0,1)之间的小数r1,(0.5, 1.0)之间的小数r2。 (1)当f≥favg,r1 (2)当f 染色体采用自然数编码,交叉运算容易产生非法染色体,但是交叉运算能产生很多新的染色体,极大地维护了种群的多样性,为更新种群、搜索到最优解做出了巨大贡献。设待交叉的两条染色体为A、B,交叉后的染色体为A'、B',交叉点为3和6,交叉结果如下: A'(0,1,3,4,5,2,1,4,5,2,3,0)B'(0,3,1,2,5,4,1,3,5,2,4,0) A(0,1,3,2,5,4,1,4,5,2,3,0)B(0,3,1,4,5,2,1,3,5,2,4,0) 2.3.3 变异运算 变异运算采用基本位变异。本文采用固定的变异概率。如果是取送结合的作业方式,在(1,染色体长度-2)之间随机产生两个变异点,交换两点的基因。设待变异的染色体为A,变异后的染色体为A',变异点为2和6,变异结果如下: 如果是取送分离的作业方式,则随机产生(0,1)之间的小数r1,当r1≥0.5时,两个变异点在(1,染色体长度/2-1)之间产生;当r1<0.5时,两个变异点在(染色体长度/2,染色体长度-2)之间产生,然后按照取送结合的变异方式进行变异。 按照改进的遗传算法,可以解决树枝型专用线取送车优化问题,算法流程图如图2。 图2 算法流程图 假设某车站衔接树枝型专用线7条,且该站仅有一台调车机车担当取送车作业。现有一批列车组要送往各专用线进行作业,各专用线作业完成之后,调车机车要将列车取回,同时回到出发点。已知调车机车到各专用线的走行时间,如表1所示。各专用线的作业时间如表2所示。 表1 调车机车到各专用线的走行时间 表2 专用线作业时间 利用遗传算法和本文提出的改进遗传算法分别求解树枝型专用线取送车优化问题,要求确定合理的取送车顺序,使得调车机车在一次完整的作业中(包括取和送)耗时最少。设种群规模为50,进化代数为100,改进的遗传算法采用本文提出的自适应交叉概率,遗传算法的交叉概率为0.8,变异概率都为0.02,对取送车分离的作业方式分别进行100次实验,算法效果对比如表3所示。 表3 两种算法对比图 由表3可以看出改进的遗传算法搜索效率和准确率明显优于遗传算法,验证了改进算法的有效性。利用改进的遗传算法求得调车机车在一次完整的作业中最少的耗时为280,同时得到多条最优取送车顺序,记录了其中的10条最优取送车顺序,如表4所示,作业时间包括机车取送车走行时间和等待作业完成时间。 由表4可以看出,虽然10种不同的取送车计划都能使调车机车在一次完整的作业中耗时最少,但是机车的走行时间却不完全相同。如果不但追求调车机车在一次完整的作业中耗时最少,而且希望机车的走行时间最少,则可以选择方案8和方案10;还可以根据专用线的具体情况选择不同的方案,因此利用改进的遗传算法求解树枝型专用线取送车优化问题利于铁路货运站效率的提高。 表4 最优的取送车顺序 本文结合树枝型铁路专用线取送车的作业特点,建立了取送结合的作业模型,而不同于以往研究者只单方面研究送车作业或者取车作业。取送结合的作业方式符合现代铁路运输的需求,同时有利于加速车辆的周转,缩短了车辆的非生产停留时间。本文改进的遗传算法提高初始种群的适应度,优良的个体在种群中被遗传的概率大,不良的个体被遗传的概率小,从而提高了算法的搜索效率。仿真实验验证了模型和算法的优越性。由此可见,利用改进的遗传算法求解树枝型专用线取送车优化问题有较大的潜力。 [1]雷友诚,涂祖耀.基于遗传蚁群算法的树枝型铁路取送车问题优化[J].中南大学学报,2011,42(8):2356-2362. [2]杨运贵,王慈光.树枝行铁路专用线取送车问题的遗传算法研究[J]. 计算机工程与应用,2008,44(12):210-211. [3]张 健,宋建业. 货物作业车取送模型的优化[J]. 铁道货运,2008,26(10). [4]余少鹤,李夏苗. 货物作业车取送模型及算法研究[J]. 铁道运输与经济,2002,24(12):46-48. [5]王雅琳,李开峰. 遗传算法在企业铁路取送调车作业优化中的应用[J]. 系统工程,2007,25(3):94-99. [6]杨 浩. 铁路运输组织学[M]. 北京:中国铁道出版社,2006:157-163. [7]周 明,孙树栋. 遗传算法原理及应用[M]. 北京:国防工业出版社,1998:11-24.2 改进的遗传算法求解树枝型专用线取送车问题
2.1 初始种群的生成
2.2 适应度函数
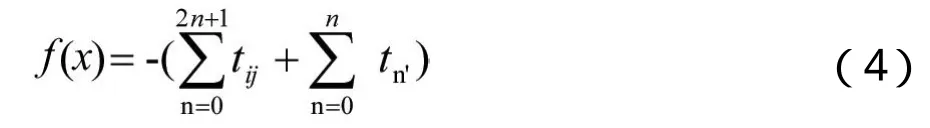
2.3 遗传操作
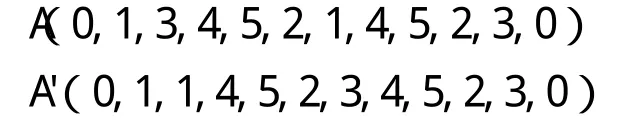
2.4 算法流程图
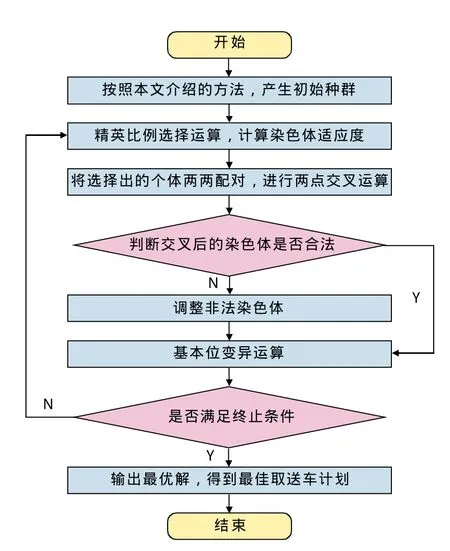
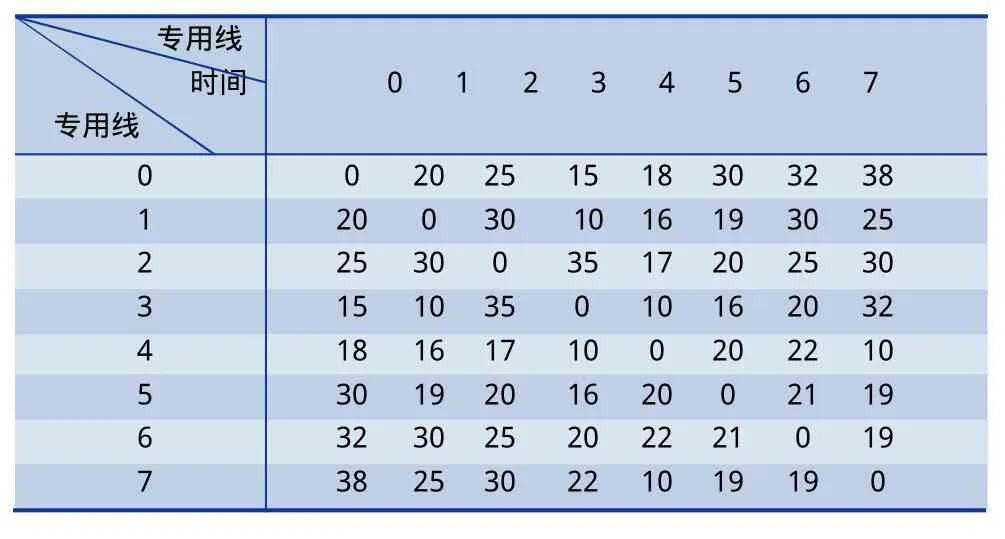
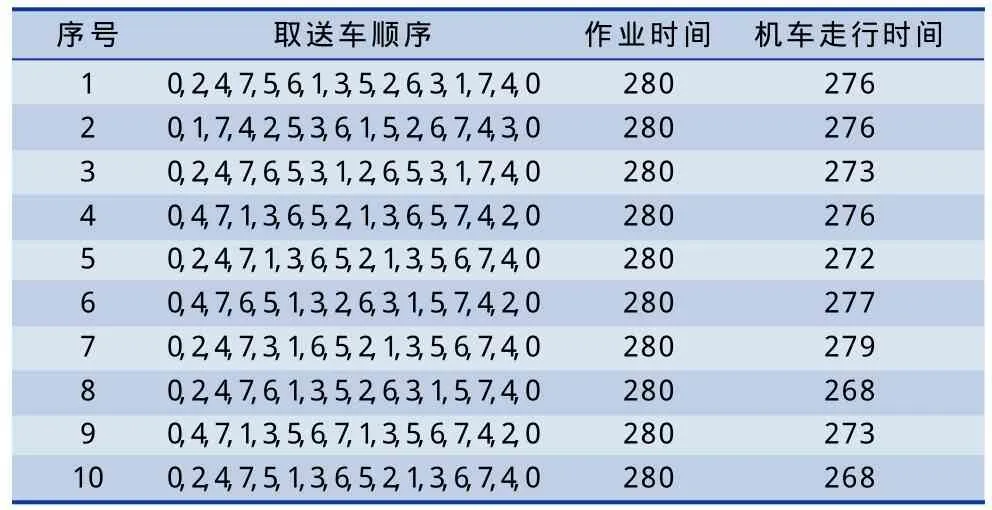
3 仿真实验与结果分析


4 结束语

