哈尔滨站售票窗口分配仿真研究

武中凯

(上海交通大学 软件工程学院，上海 200240)

哈尔滨站承担着哈尔滨铁路局 25% 的旅客运输任务和一定数量的货物运输任务。年发送旅客约2 500万人；日均图定旅客列车 91.5 对，日均发送旅客6.2万人，最高峰日发送旅客达到 11万人；日均乘降旅客 13万余人，高峰时乘降旅客达 22万人。通过分析哈尔滨站节假日(五一、十一、暑运及春运期间)的客流数据发现，哈尔滨站的客流量大、波动性强。因此，在考虑满足旅客购票需要的同时，也应考虑合理使用客运站的既有资源。

基于排队论及仿真相关理论，开发售票窗口分配仿真系统。结合哈尔滨站的实际客流情况，优化配置哈尔滨站售票资源，合理分配售票窗口，提高服务质量。

1 铁路售票排队系统特征及流程

1.1 系统特征

结合铁路客流的特点，考虑铁路旅客的到达情况，设计 M/M/c/N/∞/FCFS 型随机服务系统，系统中的数据具有如下特征。

（1）购票旅客的到达服从参数为 λ 的泊松分布，并且到达车站的时间相互独立。

（2）各窗口的服务时间服从负指数分布。规定各个窗口的服务效率相互独立，并且平均服务率 μ相同。

（3）服务台有多个，表示售票窗口数大于 1。

（4）售票厅容量为 N，当系统中购票人数 n 达到 N 时，再来的顾客被拒绝。

（5）假设旅客数量没有限制。

（6）针对排队旅客，做到先到先购票。

在实际的铁路售票排队系统中，一般 n≥c (c为售票窗口数)，系统的平均服务率为 ρ＝λ/cμ，系统状态 P0、Pn及运行指标的确定如以下公式所示。

式中：Lq为售票系统中排队等待服务的旅客数；Ls为售票系统中的旅客数；Wq为旅客在系统中排队等待的时间；Ws为顾客在系统中停留的时间。

在程序开发时，以旅客在售票系统中停留时间不超过其可接受的最大购票等待时间 T 为目标，保证服务质量，合理利用售票资源。

1.2 系统流程

售票排队系统流程如图1所示。旅客进入排队系统，首先判断各个售票窗口目前的状态，根据排队人数的多少选择售票窗口，进入该队列等待队首旅客服务结束离去，排队位置前移，继续等待。当到达队首时，开始接受服务，服务结束后离去，下一旅客继续接受服务。

2 系统开发及仿真

售票服务系统由顾客和车站两部分组成，涉及到顾客、售票窗口 (包括设备和工作人员)、车站的基础设施。系统状态变化只在时间离散时刻发生，并且具有随机性，是比较典型的离散时间系统[1]。因此，采用离散系统仿真方法对车站售票排队情况进行模拟。按照单位时间 (1 h) 内到达旅客的实际数据，模拟旅客在单位时间内到达的情况，在仿真结束后，输出开放窗口数量与平均排队时间的计算结果。

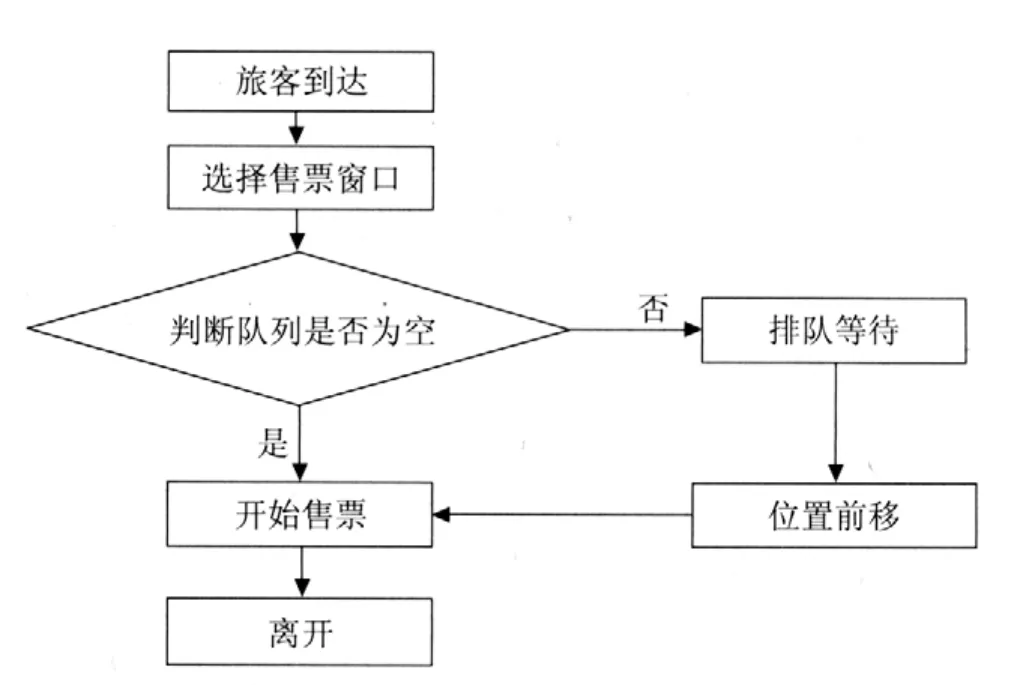
图1 旅客购票排队系统流程图

2.1 模型设计

车站售票应达到购票平均等待时间小于购票者可接受的最大排队时间。假设在极限状态下，当单位小时计时开始时，车站售票大厅已经达到饱和，即每个队列末乘客预计购票等待时间等于最大可忍受时间。由此可知，车站开设窗口数必须满足如下条件。

式中：Nq为单位小时内售票大厅排队买票人数；V为平均售票时间， min/人。

式中：T 为旅客可接受的最大购票等待时间。

由式⑴、⑵可以求得所需最小窗口数量为：

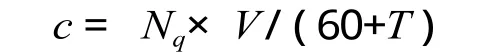
2.2 系统参数说明

2.2.1 输入参数

（1）普通旅客人数。普通旅客人数为单位小时内到达车站购买普通旅客列车车票的人数，根据实际统计数据输入。

（2）高速铁路旅客人数。高速铁路旅客人数为单位时间内到达车站购买高速铁路旅客列车车票的人数，根据实际统计数据输入。

（3）平均售票时间。平均售票时间的取值范围通常为 0~5 min，过大取值会使仿真结果误差较大，根据统计数据得到哈尔滨站平均售票时间为1 min/张。

（4）普客最大排队时长。因购票时间 (节假日和平时) 和购票时段 (早、中、晚) 的不同，普通旅客列车乘客可以接受的排队时长不同，通过调查发现，该类乘客可以接受的最大排队时长均值为15 min。

（5）高铁最大排队时长。高速铁路旅客列车乘客在不同时段可接受的排队时长不同，由于高速铁路旅客列车售票的服务质量高于普通旅客列车，通过调查发现，此类旅客可以接受的最大排队时长大约为 10 min。

2.2.2 输出参数

输出参数包括普客售票窗口数量及平均等待时间、高铁售票窗口数量及平均等待时间、增开代售点数量。对于增开代售点数量的计算，假设1个代售点可以分流替代1个售票窗口。

2.3 系统仿真

运用 Visual Basic 语言开发车站售票排队仿真系统，系统运行界面如图2所示。

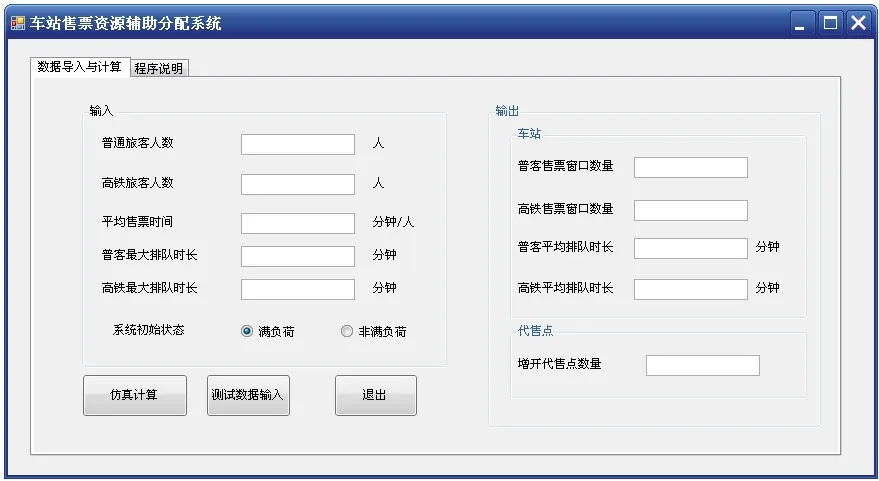
图2 售票排队辅助系统的运行界面

仿真系统初始状态分为满负荷和非满负荷 2种。满负荷即系统内旅客数量已经达到最高值，下一个进入系统的旅客需要等待最大排队时间；非满负荷即系统内旅客数为 0。仿真以旅客进入系统为触发事件，仿真过程如下。

第1步：记录该旅客到达时的系统状态，即系统内旅客人数。

第2步：判断系统状态，有空闲窗口，将等待时间记为 0；无空闲窗口，计算旅客等待时间。

第3步：系统内旅客加1人。

第4步：如果未达到指定乘客数，转到第1步；否则，停止仿真。

在仿真过程结束后，系统内仍会留有购票旅客，即部分在仿真的 1 h 内进入系统的旅客，需要等到下1个小时才能被服务。

仿真结果表明，在非满负荷状态下，平均等待时间要短于满负荷状态。在考虑随旅客人数增减售票窗口的情况下，系统中时刻都可能出现接近满负荷的状态，因此，满负荷状态的仿真更接近实际情况。如果仿真结果显示车站的既有售票窗口不能满足需要，则需增加售票窗口数量，并优先开设高铁售票窗口。

3 仿真计算分析

以 2010年“五一”期间哈尔滨站售票厅的售票情况为例，计算售票窗口需求数量。哈尔滨站实际售票窗口数为 33个，售票大厅开设 30个窗口，动车组售票厅开设3个窗口，并且不再扩建，当不能满足需要时，则应增加售票点的设置。车站平均售票时间为 1 min/ 张，高铁购票人数约占总购票人数的 30%。调查所得售票厅排队购票旅客数量如表1所示。从0:00—24:00，每小时设为1个时段。

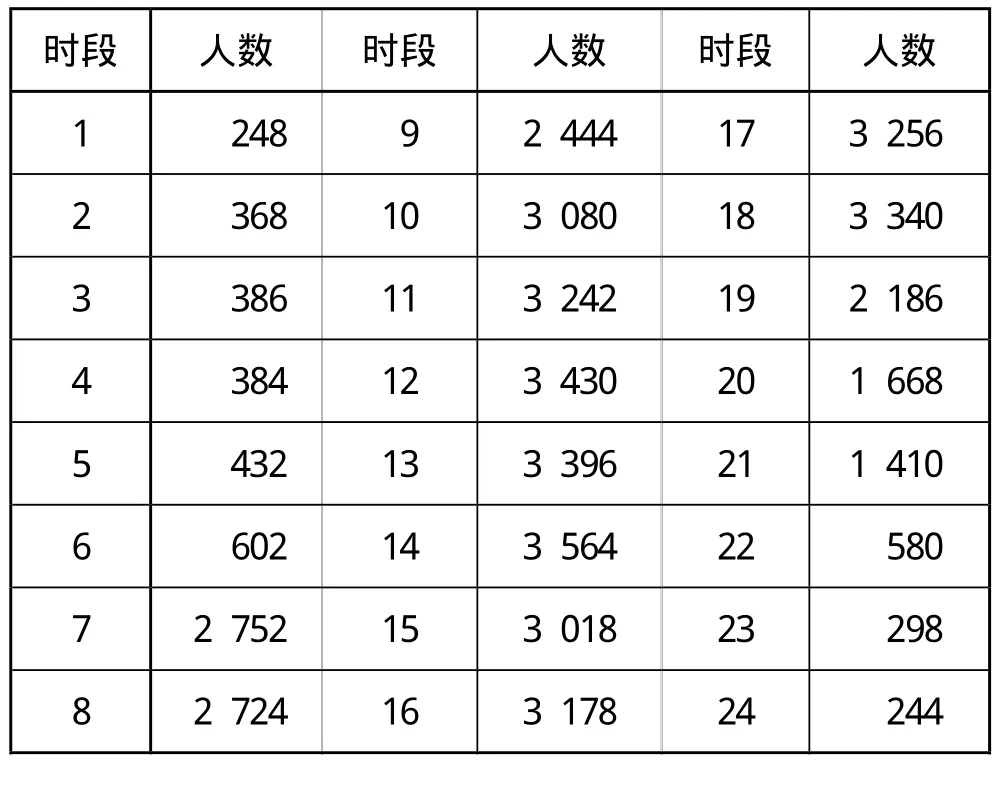
表1 2010年“五一”期间哈尔滨站各时段售票大厅旅客排队人数

选取表1中 6:00—18:00 这个时段，即时段 7—18，进行模拟仿真，得到如表2所示的指标计算结果。受哈尔滨站资源限制，站内售票窗口不能满足某些时段的购票需求，因此，需要在哈尔滨市内增设售票点，或在车站附近增加临时售票窗口，以满足旅客需求。

从表2可以看出，普通旅客列车与高速铁路旅客列车售票窗口的平均排队时间均不超过各自旅客可接受的最大排队时间，能够最大化满足购票需求，有效利用车站资源。因此，车站可以根据排队人数，合理开设售票窗口数量。如果出现车站售票资源不足的情况，可以增开代售点。

在窗口设置上，高铁售票窗口与普客售票窗口分开，可以保证高铁售票服务的质量。高铁售票窗口一般在固定几个时段开放，在其他时段，这些窗口也可以为普通列车售票服务，保证售票工作顺利进行。

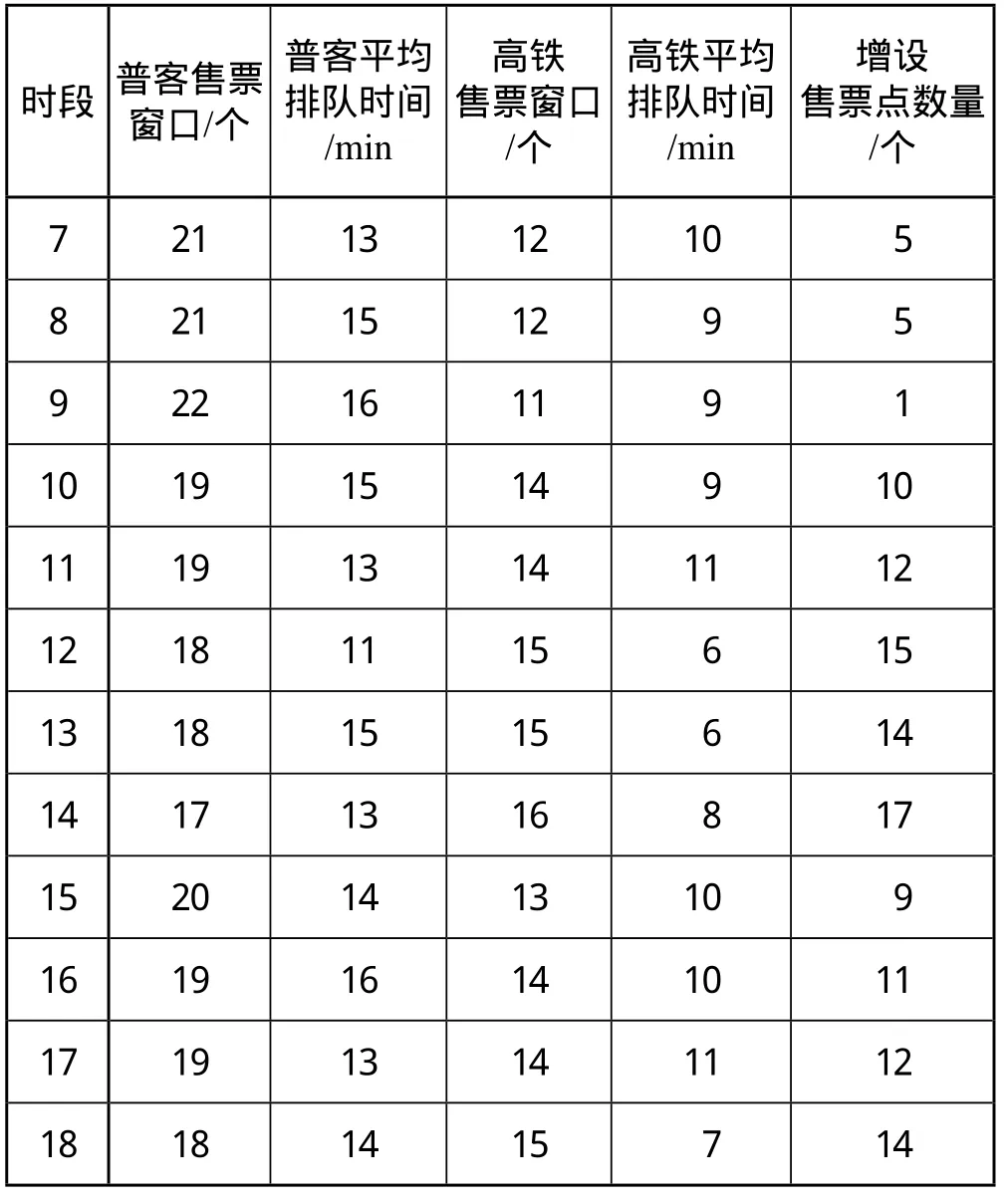
表2 仿真结果

4 结束语

基于排队论建立车站售票排队服务系统模型，选用VB语言开发系统仿真软件。以哈尔滨站为例，根据实际到达的旅客人数计算需要开设的窗口数量，以保证旅客平均等待时间不超过最大接受排队时间，合理利用售票资源。

[1]徐瑞华. 运输与物流系统仿真[M]. 上海：同济大学出版社，2009.