基于整数规划模型的高速客运站选址方案及数量研究

姜大元

（中铁第四勘察设计院集团有限公司 线站处，湖北 武汉 430063）

0 引言

铁路枢纽客运站选址及数量确定是一个复杂的系统工程。在进行铁路枢纽规划或线网规划时，通常需要对枢纽内的既有客运站及旅客出行分布情况进行全面的综合分析，从整体上系统地确定枢纽内客运站的位置及数量，从而最大化地发挥客运站的功能，方便旅客乘车，节约社会资源和建设投资。设置较多的客运站可以方便旅客出行，有利于吸引更多的客源，但设备分散、投资大，不利于管理和利用，同时需要大量的社会资源与之配套，而且旅客换乘不方便；如果客运站设置过少，虽然旅客换乘方便，客运设备集中，便于管理和使用，但运输组织干扰严重，客流集中组织困难，易造成局部交通拥堵等问题。因此，合理确定枢纽内高速客运站的位置及数量，更好地优化枢纽内客运站布局，是大城市铁路枢纽规划的重要问题之一[1-2]。

目前，铁路枢纽规划及设计实践大多根据设计者的经验，人为及主观因素较多，尚无定量确定枢纽内高速客运站选址及数量的评判方法。因此，建立数学模型，科学、定量确定枢纽内高速客运站位置及数量成为亟待解决的课题。为此，利用整数规划模型，从建设成本、运营成本、枢纽客运站设计能力、城市规划等因素综合考虑，科学确定枢纽内高速客运站的位置及数量方案。

1 模型的建立

在铁路枢纽换乘的旅客，其出发地、目的地多种多样，与所有铁路客运站构成一个复杂的系统，为使模型不过于复杂，又能具有广泛的代表性，从而方便研究，对系统进行以下简化[3-4]。

（1）由于枢纽内相当长的一段时间 (一年或更长) 内，出发与到达的单向客流量基本相等，因此可以只考虑从枢纽吸引区域出发的单向客流。

（2）中转客流对于枢纽的规划影响较大，为简化模型可以将枢纽内每个客运站作为一个出发地。

（3）以旅客出发数量相对集中的长途汽车站、公共汽车站、大型企业单位、居民区、铁路客运站等为出发地进行细化。由于旅客出行目的地众多，为简化计算，将枢纽衔接方向上的第一站作为此方向上的总目的地，因为每种方案从该站到旅客真正目的地的运输费用是相同的。

（4）由于目前高速铁路引入枢纽多采用高速、普速分站作业形式，因而以此为基础，对高速铁路客运站选址及数量进行研究。

综上所述，可将不同出发地、目的地旅客径路简化[5]，如图1所示。

图1 不同出发地、目的地旅客简化径路示意图

从经济最优的角度出发，目标函数要求高速客运站选址应满足旅客集散费用、客运站基本建设费用及建成后运营费用、社会综合费用之和最小[6]。因此目标函数可以表示为：

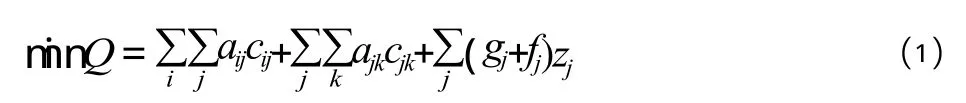
式中：i 为目的地序号，i＝1，2，…，m；j 为客运站编号 (含拟建的高速客运站)，j＝1，2，…，n；k 为出发地序号，k＝1，2，…，l；aij为年均每日从客运站j 至衔接方向 i 的客流量，人次/d；ajk为年均每日从出发地 k 至客运站j 的客流量，人次/d；cij为从客运站j 至衔接方向第一站 i 的人均交通费用，元/人；cjk为从出发地 k 至客运站j 的人均交通费用，元/人；gj为客运站j 的日均基本建设费用，元/d；fj为客运站j的日均运营费用，元/d；zj为选择参数，zj＝{0，1}，若新设高速客运站站址与备选站址相同时 zj取 1，否则取 0。

客运站的任务是将集中于客运站的旅客全部运送到指定的目的地，因此客运站的旅客发送量应与集中于客运站的旅客总量相等，即：

客运站设计的总规模应满足客运需求，即设计日均旅客到发量应大于客运站实际办理的日均旅客到发量之和：

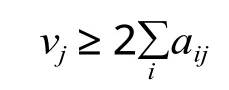
式中：vj为客运站设计的最大日旅客发送量，人次/d。枢纽内需设置的客运站数量为：j∑zj≤r

式中：r为枢纽内应设置的客运站数量，该数量不大于总图规划的客运站数量，即 r≤n。

对于枢纽内既有的客运站，为充分利用既有设置，节省工程投资，按保留考虑。因此，

式中：S为既有客运站组成的集合。

模型中cij、cjk、aij、ajk、gj、fj、vj可以通过统计、分析、调查等方法确定，zj需人为确定。

2 参数的确定

参数的选择是否合理对于模型能否得出正确的结论影响重大，由于枢纽吸引范围内旅客出发地、目的地众多且分散，因此精确确定每一出发地、目的地至客运站的参数极为困难，故可参考公路运输OD 调查法并结合铁路已有的统计数据，采用以下方法确定模型参数。

2.1 aij、ajk 的确定

年均每日从出发地 k 至客运站j 的客流量 ajk可按以下方法确定。

（1）将枢纽内旅客出发较集中的长途汽车站、公共汽车站、大型企业单位、居民区、铁路客运站作为出发地，而其他区域分成若干小区，以每个小区的中心作为出发地。

（2）通过发放旅客出行意愿调查表等方式确定区域内人均旅客乘车系数，并根据政府及有关部门的人口统计数据和规划资料确定服务区内常住总人口数，由以下公式算出每个出发地辐射范围内的年均日出行旅客量 Qk：

式中：Ak为出发地 k 吸引范围内人口总数；Fk为出发地 k年平均乘车人数，次/人；Fk的大小取决于当地经济发展水平和人们的出行习惯，可参照统计资料和发展因素综合确定；ajk由出发地 k 至客运站j的所有出行人数乘以选择铁路出行的比重得出。

aij可根据铁路统计资料，并根据实际情况进行适当修正确定。

2.2 cij、cjk 的确定

（1）cij可通过客运站j 至 i 方向上第一站的铁路票价和去往该方向的客流统计资料计算得出。由于铁路存在不同等级的列车，因此可以根据以往的客流统计资料，采用加权平均的方法计算平均每人从枢纽客运站j至衔接方向第一站i的交通费用 cij。

拟建客运站至其衔接方向第一站的交通费用可根据该线引入后转移的客运量与新增客运量之和乘以该方向不同等级列车票价加权平均计算。

（2）每人从出发地 k 至客运站 j 的交通费用 cjk可以根据出发地 k 至客运站j 的各种交通运输方式的乘车费用乘以其相应的乘车人数加权平均确定。

2.3 vj的确定

新建高速客运站设计日均最大旅客发送量 vj应根据经济及运量调查的客流量预测结果，并结合该地区的经济发展水平，综合考虑该客运站的作业性质，通过比较分析确定。既有客运站的最大日旅客发送量等于其设计能力与可行的改扩建规划能力之和。

2.4 gj 的确定

根据《铁路基本建设工程投资预估算编制办法》对不同站址方案按同等精度进行站前、站后主要工程估算，汇总得出总费用 F，经济评价计算期取 25年，可得到客运站日均基本建设投资费用，其计算公式为：

2.5 fj 的确定

客运站日均运营费用 fj可选取客运站日常运营所需要的关键费用，如人员工资、管理费、设备运营维护费、日常修理费、水电费、税费等。各选址方案的运营费用计算方法及相关参数应相同，相同部分可省略。

新建高速客运站数量应按照以下原则确定[7]。

3 高速铁路条件下模型的修正及求解

3.1 新建高速客运站数量的确定

（1）新建高速客运站的个数不超过枢纽内应设置的客运站数量。

（2）新建高速场与既有站并站或高架在既有站之上，或者在既有站地下新建高速场，因工程量大，普速场与高速场相对独立，客运设备也自成系统，故按照2个车站计算。

（3）新建高速线按线路别引入既有高速站的，对既有车站客运设备无改动或改动较小的，只按1个车站计算。

（4）枢纽内既办理客运作业也办理货运作业的车站，只计算其客运能力，并按1个既有客运站计算。

3.2 模型的求解思路

设既有客运站集合 S 的元素个数为 nj，则拟建高速客运站的数量为 r－nj，模型的求解思路如图2所示。

图2 模型的求解思路

4 模型的计算

在确定模型中涉及的参数后，建立枢纽客运站布置的整数规划模型，应用枚举法求解，可计算高速客运站不同布置方案的总费用 Q，取 Q较小的若干方案作为备选方案，Qmin方案为理论最优方案，其计算步骤如下。

（1）为方便计算，可假设备选新建高速客运站个数为 r (从r＝nj开始，r≤n) ，共有种方案组合，得到拟建客运站数为 r 情况下的满足约束条件的方案集 Dr，并计算每种方案的总费用 Q。

（2）增加拟建高速客运站的个数，计算客运站数在 r＋1个情况下的总费用，重复步骤 1，得出客运站数为 r＋1 情况下且满足约束条件的方案集Dr＋1和在此条件下每种布置方案的总费用 Q，如此循环，直至 r＝n。

（3）比较方案集 Dr(r＝1，2，…，n) 中每种方案总费用 Q，Qmin方案可作为近似最优方案，此方案可作为高速客运站设计选址的备选方案，为避免偶然错误，取 Q 较小的几个方案组成下一步研究备选集 D，可再进行下一步必要的甄选。

在大型枢纽有多个客运站、备选的方案又较多时，模型参数的确定和费用指标求解过程计算工作量巨大，因此可在模型、参数确定后，利用计算机技术根据整数规划模型计算方法和步骤编制程序，以提高求解精度和计算效率。

5 算例

某地区铁路枢纽如图3所示，既有线衔接4个方向，Z1、Z2、Z3为枢纽内3个既有客运站，现有1条高速铁路即将引入该枢纽。结合城市规划，选定了 B1、B2、B3、B4共4个备选站址。

既有客运站集合 S＝{Z1，Z2，Z3}；备选站站址集合B＝{B1，B2，B3，B4}；出发地集合 D＝{d1，d2，…，d17}；所衔接的方向上第一站集合Q＝{Q1，Q2，…，Q6}。

根据文中的原则通过调查依次确定cij、cjk、aij、ajk、gj、fj、vj，针对每个方案组合依次按模型公式依次求得每种方案的总费用，并判定是否满足约束条件，选择满足约束条件且总费用最小的方案作为近似最优解。现以方案S14'＝{Z1，Z2，Z3，B1}为例进行说明，其他方案的计算方法相同。

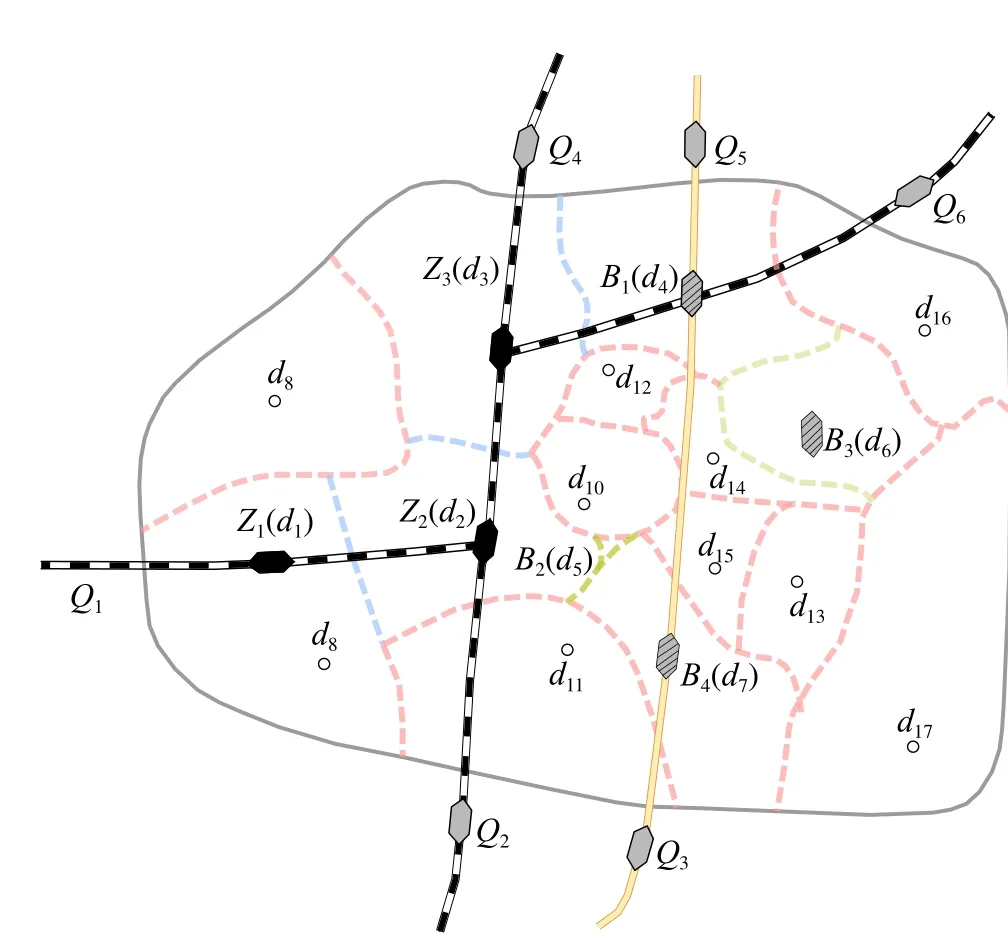
图3 某地区铁路枢纽

5.1 aij、ajk的确定

（1）ajk的确定。根据统计及规划部门的资料得dk吸引范围内的人口总数 Ak，结合当地经济发展水平、出行习惯确定出发地k的平均乘车人数Fk，根据式⑵，得出各出发地的乘车总人数，再根据 dk吸引范围内所有乘车人数乘以选择铁路出行的比重并结合铁路客运站衔接方向的分工确定得出ajk，详见表1。

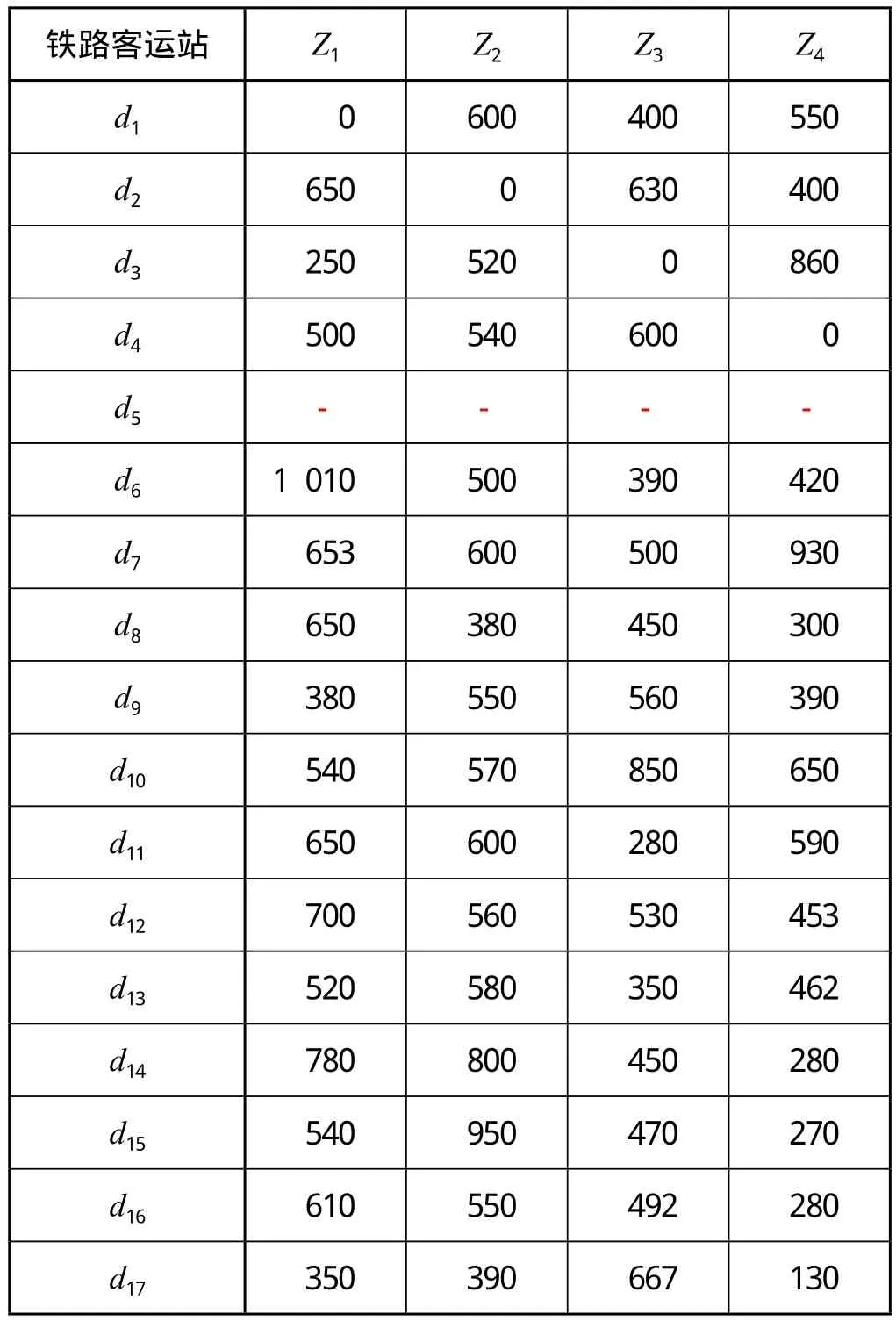
表1 铁路客运站年均旅客发送量 人/d

（2）aij的确定。根据铁路部门的统计资料，得到 aij如表2 所示。

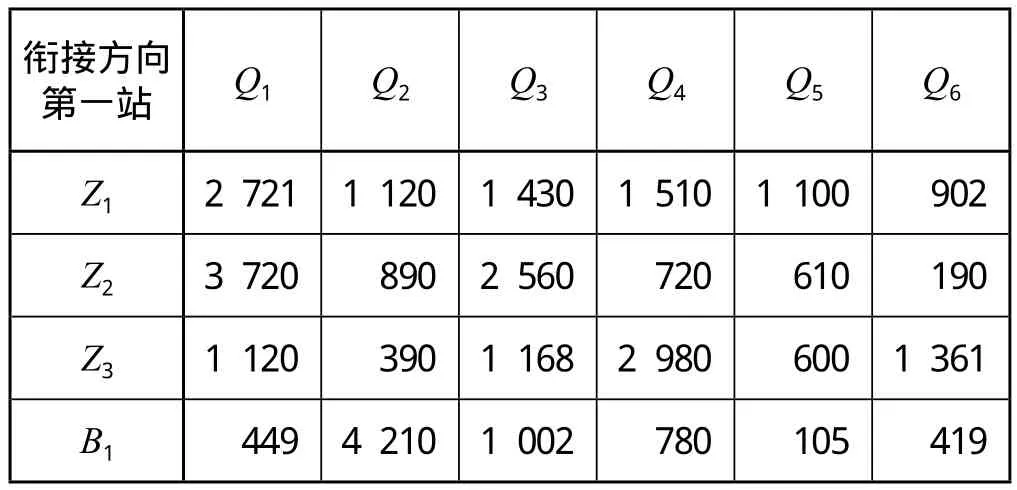
表2 铁路客运站至衔接方向的旅客量 人/d

5.2 cij、cjk的确定

（1）cij的确定。根据客流统计资料，采用加权平均方法得到 cij值，汇总见表3。

（2）cjk的确定。通过调查，计算从各出发地到各客运站的平均乘车费用 cjk，详见表4。

5.3 vj的确定

根据 B1的站址面积及客流量预测，结合该地区的经济发展水平，综合考虑该客运站的作业性质，通过比较分析确定。得到：v1＝15 000人/d，v2＝12 000人/d，v3＝18 000人/d，v4＝19 000人/d。

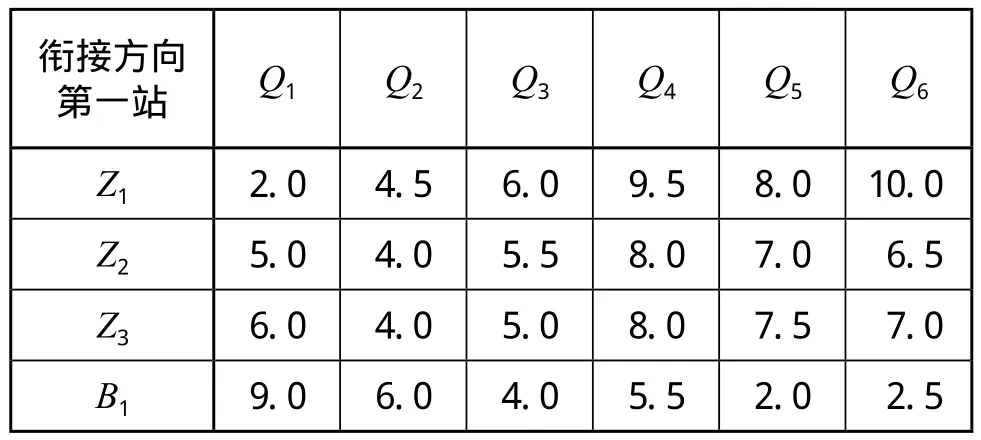
表3 客运站到衔接方向第一站的平均乘车费用 元

表4 出发地到铁路客运站平均乘车费用汇总表 元

5.4 gj的确定

根据《铁路基本建设工程投资预估算估算编制办法》，确定 B1的总工程费用为 35.2 亿元，据式⑶计算：g4＝35.2×10 000/(25×365)＝48.2(万元/d)，同理可求出：g1＝24.5(万元/d)，g2＝19.6(万元/d)，g3＝32.1 (万元/d)。

5.5 fj的确定

参照国内外与 B1规模等级类似的车站，计算相关要素总费用，并确定日均总费用4=30.7(万元/d)，同理可以求出：f1＝21.3(万元/d)，f2＝15.8(万元/d)，f3＝27.8(万元/d)。

5.6 模型计算

确定所需的各项参数后，根据式⑴计算各方案总费用，并检查是否满足约束条件，计算结果见表5。

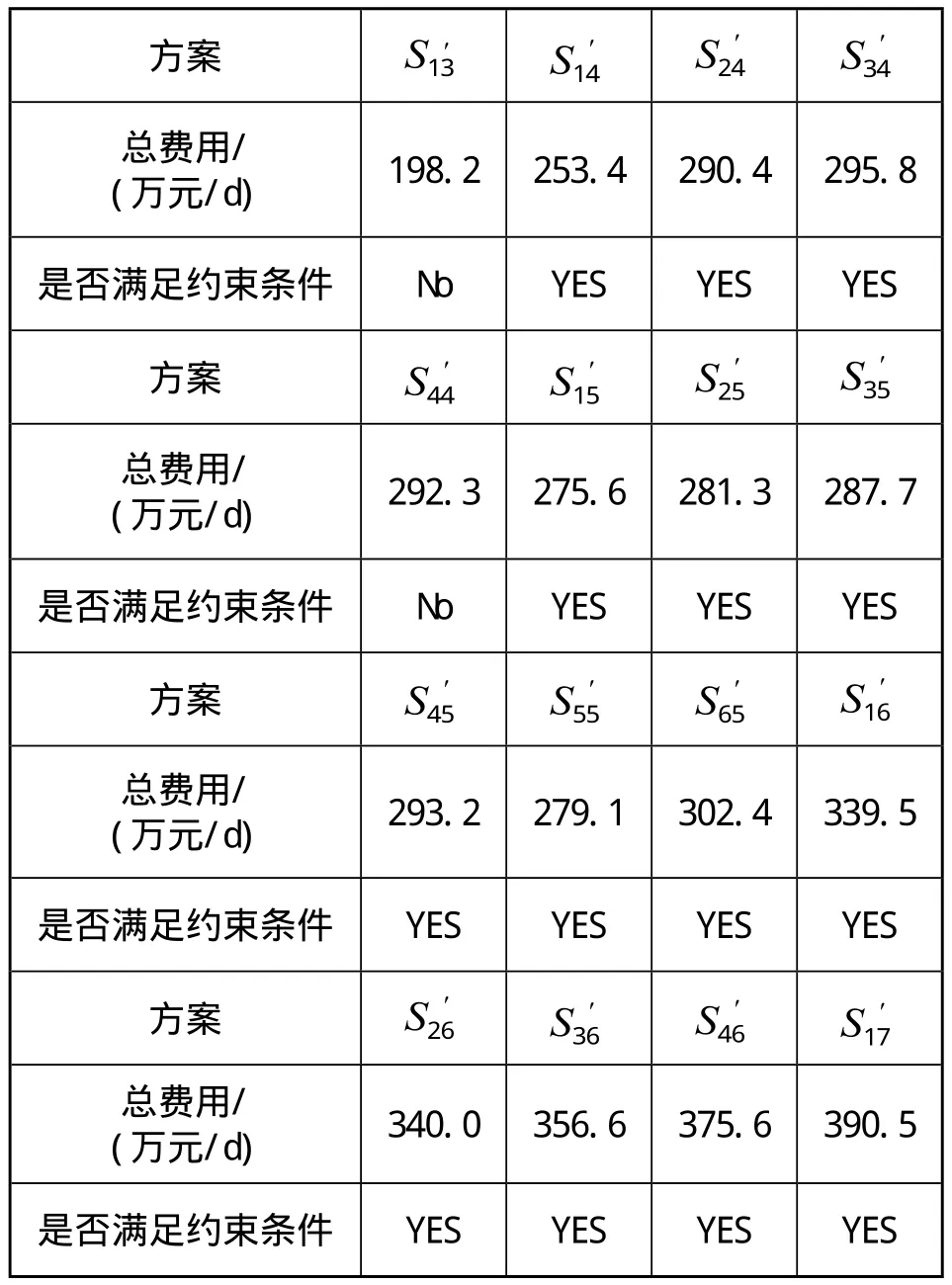
表5 各布置方案总费用及约束条件检验表

6 结论与建议

整数规划模型将整个枢纽客运系统作为一个整体考虑，以工程建设费、日常运营费、旅客集散费等总费用最小作为评判标准，兼顾了铁路与旅客的双方利益，为确定枢纽高速客运站的初步位置及数量提供一种新思路，可为枢纽总体设计决策时提供参考。

运用整数规划模型确定高速客运站初步位置及数量时，确定参数值的工作比较烦琐，需要进行大量的调查分析，参数值确定得越准确，计算的结果对枢纽客运站规划与设计就越有参考价值，由于模型维数多，求解过程计算工作量很大，因此应采用计算机辅助计算以提高求解效率。

该模型以费用最小作为惟一评判指标，没有考虑高速客运站布置的其他影响因素，因此所求的最优解只能认为是近似最优解，对此可以通过这一模型得到几个相对比较优的方案作为备选方案，然后利用其他数学模型 (如 AHP-FUZZY 模型等) 进行甄选，以保证最终方案科学合理。

[1]王 南，朱志国，胡 岩. 客运专线条件下铁路枢纽客运站布局优化[J]. 同济大学学报，2005，33(5)：631-634.

[2]陈焕江. 公路铁路客运站布局和选址方法的研究[J]. 公路交通科技，2001(6)：109-112.

[3]李旭宏. 城市交通方式预测实用方法研究[J]. 东南大学学报，1997(6)：138-141.

[4]徐永能，李旭宏，朱彦东，等. 走廊内各交通方式优化组合模型分析[J]. 交通运输系统工程与信息，2005(4)：36-38.

[5]刘灿齐. 现代交通规划学[M]. 北京：人民交通出版社，2001.

[6]陈应先. 高速铁路线路与车站设计[M]. 北京：中国铁道出版社，2001.

[7]Yoshihiro AKIYAMA.High-speed Railways in the World[J].Japanese Railway Engineering，1994，3(3)：34-38.