高速铁路列车运行图的均衡性研究

鲍晶晶，徐培娟

（西南交通大学 交通运输与物流学院，四川 成都 610031）

1 列车均衡性的定义及意义

列车均衡性是列车运行图评价的重要指标之一。列车运行线分布是否均衡是评价列车运行图编制质量的主要指标，尤其是列车在车站到发的均衡性，将直接影响车站通过能力和作业进程、运行图的稳定性和运营调度、列车的区段旅行速度和动车组 (机车) 的运用，以及车站设备的合理利用等质量指标。

目前，关于既有线列车运行图均衡性的研究，主要有在给定列车运行图情况下，运用偏差和偏差离差建立评价矩阵，通过模糊决策矩阵完成对运行图均衡性的综合评价[1]；运用标准偏差和相对标准偏差对某一技术站列车的到发均衡性进行分析量化[2]；提出用列车相邻间隔方差和相间间隔方差来描述既有线列车运行图的均衡性[3]。

由于高速铁路旅客需求的多样化，客流在时间上有较大的波动性，在铺画高速铁路列车运行图时，不仅应满足旅客全天对出行的需求，更应突出高峰时段、节假日期间的通过能力。因此，既有线列车运行图均衡性评价理论和评价方法不能满足高速铁路列车均衡性的要求，应通过结合高速铁路独有特点，建立高速铁路列车均衡性评价体系。在研究中，主要将列车运行图中涉及的两类列车按其速度高低分为 A 类列车与 B 类列车。

2 高速铁路运行图均衡性描述

在对既有铁路列车运行图的均衡性评价中，时间范围都是以列车运行图的 24 小时为标准来评判列车运行图的均衡性[2]。而高速铁路列车运行图是一张非闭合的列车运行图，由于线路检修的需要，并考虑电气化铁路施工和高速铁路列车运行的特点，一般在夜间预留 4～6 h 矩形施工“天窗”，在天窗时间内没有列车运行。另外，在一天中存在因旅客出行需求造成的高峰时段和平峰时段。因此，在扣除天窗时间的基础上，将高速铁路列车运行图划分为几个高峰时段和平峰时段，分别考虑计算其均衡性。以高峰时段的 A 类列车为例，计算列车运行图的均衡性指标。

列车运行图中存在 H个高峰时段，设第 h个高峰时段的时间为 Tg,h，该时段的时间范围为：

设高速列车运行图上某一高速铁路车站 O，A 类列车在高峰时段 Tg,h的出发时刻集合记为：到达时刻集合记为：，其中，nh、mh分别为 O 站高峰时段 Tg,h中A类列车出发和到达的数量。

以出发列车为例，设集合XFHA，O为升序排列，使其满足其中i代表Tg,h时段内从O站出发的 A 类列车。

2.1 A 类列车在O站高峰时段发车间隔偏差及偏差离差

Tg,h时间段内相邻两列 A 类列车的发车时间间隔为：应满足约束条件：

则 O 站在高峰时期 Tg,h内相邻 A 类列车发车间隔时间为：

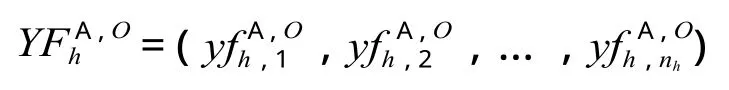
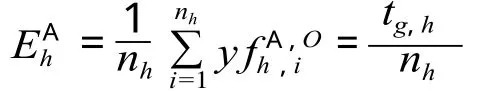
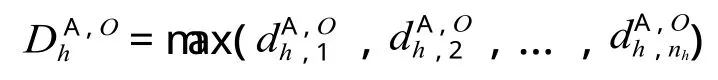
是

偏离均值

的最大程度，称为

的偏差，这样可以计算出 A 类列车出发的均衡性。显然

越大，表示

偏离均值

的程度越大，即 A 类列车出发时刻

的时间间隔波动性越大，但

越大，只能代表列车运行图中某一个或几个元素的偏离均值越大，而不能完整地描述该时段内所有列车的均衡性，于是引入偏差均值和偏差离差的概念：

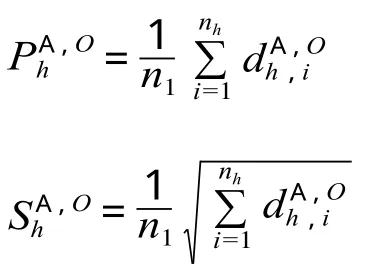
如图1所示，虽然两图的发车间隔偏差相同，但图1 a 中列车铺画的均衡性更好。因此，由求解和的公式可以看出，其值大小只与有关，与的排列次序无关，不能反映 A 类列车发车间隔的排列次序。

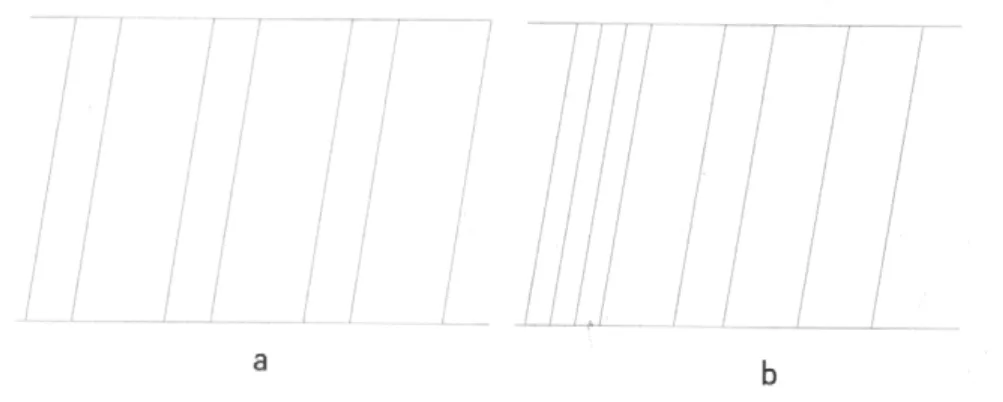
图1 列车发车间隔示意图

2.2 A类列车在 O 站高峰时段发车相间间隔偏差及偏差离差

将列车发车间隔的排列顺序考虑在内，引入一个列车发车相间间隔分布来描述列车发车间隔的排列顺序：

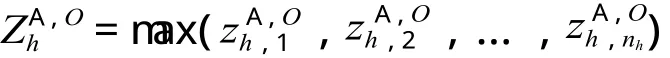
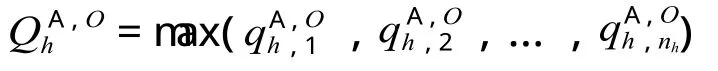
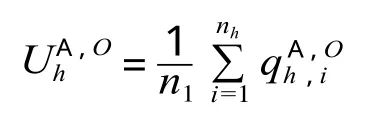
2.3 高峰时段 A 类列车在O站发车的均衡性评价指标体系

通过计算可以得出 O 站在第 h个高峰时段 Tg,h内，A 类列车的均衡性评价指标由此建立 A 类列车在各个高峰时段的均衡指标矩阵：

根据列车运行图，统计出全天各高峰期内A类列车发车次数的行矩阵：N＝(n1，n2，…，nH)，根据加权平均原理，计算总高峰期 A 类列车发车均衡性的总评价指标用矩阵 AG表示：

2.4 A 类列车在 O 站全天的发车均衡性指标

与既有铁路相比，高速铁路需要较好地应对客流高峰期，实现客流高峰期高密度、高速度、高安全运营，在对高速铁路列车运行图的均衡性评价中更看重客流高峰期的列车到发时间安排，因此在计算 A 类列车高峰时段和平峰时段均衡性指标的基础上，根据实际需求分析和专家评价，对高峰时段给予权重 α，平峰时期的权重为 (1－α)，则 A 类列车在O 站全天(综合维修天窗除外)的发车均衡性指标 (DA,O，PA,O，SA,O，QA,O，UA,O，RA,O)，用矩阵 A 表示：

2.5 全天 O 站均衡性综合评价指标

由于高速铁路采用 A 类列车和 B 类列车混合运营模式，根据上述原理，将 B 类列车按高峰时段和平峰时段分别计算出发间隔和相间间隔偏差及偏差离差，通过加权平均、赋值权重方法，得到 B 类列车在 O 站的均衡指标 (DB,O，PB,O，SB,O，QB,O，UB,O，RB,O)。

图2为 A、B 类列车铺画示意图，在图2 a 中A、B 类列车是集中到发，在图2 b 中 A、B 类列车是成组交替到发。在相同的开行对数下，为满足旅客在同一时间段内对不同种类列车的需求，图3 b 的铺画方案更加合理，同时能节省机车车辆。因此，在考虑同类型列车发车均衡性的同时，也要考虑不同类型列车相互协调的整体均衡性，即在划分高峰时段和平峰时段的基础上，不考虑列车等级统一进行均衡性分析，同理，得到不同类型列车在 O 站的均衡性指标 (DAB,O，PAB,O，SAB,O，QAB,O，UAB,O，RAB,O)。

图2 A、B类列车铺画示意图

通过以上分析论证及计算，得到 O 站发车均衡性指标，包括 A 类列车发车均衡性指标、B 类列车发车均衡性指标，以及 AB 类列车发车均衡性指标，根据以上3个指标系建立 O 站的发车均衡性指标矩阵FO¢：

运用层次分析法，建立 A 类列车、B 类列车、AB 类混合列车均衡性相对重要度的判断矩阵，通过相对重要度计算和一致性检验，得到 A 类、B类、AB类列车的均衡性重要度权重 W：

计算 O 站全天发车的综合性均衡指标：

同理，对 O 站的到达列车按以上原理分析计算，得出 O 站到达列车的均衡性指标 OD：

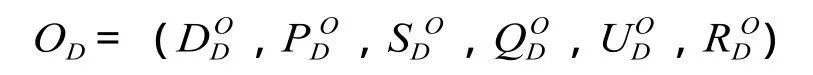
对于 O 站，到达列车和出发列车的数量一般不相同，设出发列车和到达列车的总数分别为 N、M列，根据到发列车的比重，计算 O 站接发列车均衡性综合指标 OZ：

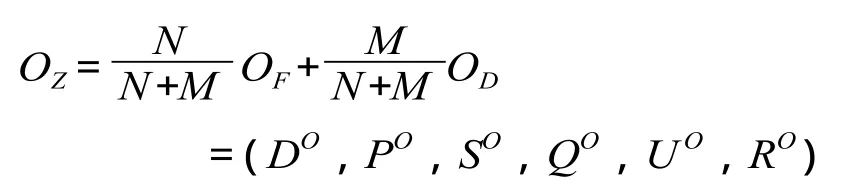
因此，可以根据 O 站的各均衡性指标来衡量列车到发的均衡性，该指标越小，列车到发的分布越均衡；反之，列车到发越不均衡。

3 高速铁路运行图列车均衡性评价方法

3.1 评价指标矩阵

列车运行图的均衡性需要将沿途各站的列车到发的均衡指标考虑在内。因此，可考虑将列车运行图中起始站和重点中间站分别计算相关均衡性指标D、P、S、Q、U、R，组成评价指标矩阵：

评价一个客流区段高速列车运行图的均衡性，需要对矩阵 G 中各元素gij(i＝1，2，…，6；j＝1，2，…，6) 进行综合处理，得出评价运行图均衡性是否满意的评判点PB，根据评判区间[0，1]，评价评判点 PB在区间的位置，得出列车运行图均衡性的优劣。例如，0≤PB＜X1时，为不满意；X1≤PB＜X2时，为较满意；X2≤PB≤ 1时，为满意。其中，X1和 X2可以通过专家和决策者打分得到。

3.2 决策矩阵

得到列车运行图均衡性描述的指标矩阵后，还需要一个决策矩阵，即为指标矩阵中的每一个元素 gij赋予一个评价标准[3]。这个标准可以由专家和决策者通过对线路通过能力利用率、旅客列车开行数量等的总体考虑，根据其性质和作业量，对每一个指标建立以物理性数据为论域的决策者满意程度的模糊集合。现以 gi1为例，讨论以偏差为论域的满意程度模糊集合

如图3所示，当gi1(即D) ≤Da时，满意程度为1，即决策者完全满意；当 Da＜gi1＜Db时，决策者的满意程度在 (0，1) 区间内；而当 gi1≥Db时，满意程度为 0，决策者完全不满意。其中，Da、Db的取值可以根据高峰时段与平峰时段客流需求差，列车平均最小间隔时间，列车平均缓冲时间，通过能力利用率，A、B 类列车开行比例等因素，由专家在分析以往列车运行图的基础上确定。

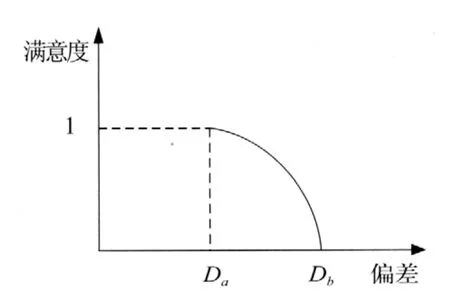
图3 满意度偏差示意图

由此，可以得到关于 gi1的模糊评判集合。同理，可以得到 gi2、gi3等各因素的模糊评判集合。从而得到评判决策矩阵A为：

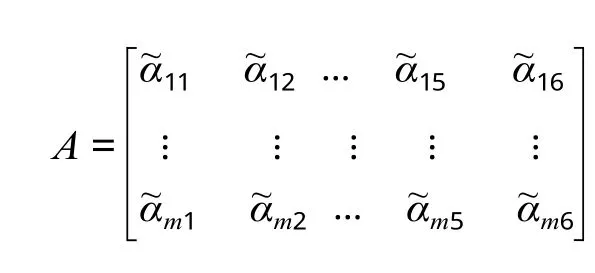
得到区段内均衡性评价的指标矩阵和决策矩阵后，可以计算区段在 Ti时间段内的均衡性满意程度。其计算步骤如下。

（1）根据每个车站的性质和任务，通过专家打分和统计分析相结合的方式，建立列车运行图指标矩阵中各项指标的权重系数bk(1≤k≤6，且k 为整数)。同理，建立区段内各车站的权重系数kb¢(1≤k≤m，且 k 为整数)。

（2）对于每个指标的模糊评判集合α~ij，都满足当 gi1(即D)≤Da时，满意程度为 1，即决策者完全满意；当 Da＜gi1＜Db时，决策者的满意程度在(0，1) 区间内；而当gi1(即D)≥Db时，满意程度为0，决策者完全不满意。令 ω＝(Db－Da)/n (其中，n的取值根据对均衡性评判的精度要求而定)，则 gij所对应的满意度评判值fij的计算公式为：

当 gij≤Da时，fij＝1

当 Da＜gi1＜Db时，fij＝

当 gij≥Db时，fij＝0

（3）对于每个车站计算均衡性的评判值 Ci的计算公式为：

计算运行图在时间段 Ti上的均衡性评判值 PB：

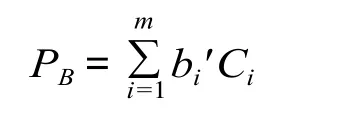
依据评判度 PB落入区间 [0，1]的位置，给出高速列车运行图的均衡性评判结果 (满意、较满意和不满意)。

4 结束语

通过以上分析，针对高速铁路的运营特点，对列车运行图的均衡性进行评价研究，将列车类型分为 A 类、B 类和 A、B 类混合型三大类，并综合考虑列车运行图服务质量的评价要求和适应性，将列车运行图的均衡性评价研究分为高峰时段和平峰时段，分别计算列车出发及到达的6个均衡性指标，建立指标模糊评价矩阵，确定相应权重，计算列车运行图的均衡值。研究提出的均衡性评价指标体系符合高速铁路运营的特点及性能，能更加准确地对列车运行图均衡性进行评价。

[1]史 峰，邓连波，黎新华. 客运专线相关旅客列车开行方案研究[J]. 铁道学报，2004，26(2)：16-20.

[2]何知明. 客运专线列车运行图的评价研究[D]. 成都：西南交通大学，2009.

[3]彭其渊，张羽成，李 孟. 列车运行图均衡性评价方法研究[J]. 西南交通大学学报，1998(8)：14-19.