列车区间运行安全的Petri网模型研究

李智基，代振环，张春民

（兰州交通大学交通运输学院，1.硕士研究生；2.副教授，甘肃 兰州 730070）

列车在区间的运行是一个循环过程，即在一定的闭塞条件下，列车在区间运行时由一个闭塞分区运行到前方另一个闭塞分区。在这个过程中，司机对列车在区间的行车状态需要不断地判断，并对设备可能出现的状况采取相应的措施，以保证行车安全。可见，列车区间运行安全的系统涉及了司机和多项行车控制设备，具有相对动态和复杂性、整体性的特点。由于列车在区间运行的安全直接影响着铁路的运输能力，以及列车运行的安全正点等，对铁路运输生产任务的完成起着决定性的作用，为此，研究列车区间运行安全问题具有重要的现实意义。

目前，对铁路事故安全的分析方法较多，如灰色关联分析法、事故树分析法、Petri网等[1-6]。灰色关联分析法是对系统动态发展过程态势的比较分析，即通过对有限的事故结果分析，从总体上得到对事故特性的认识，适用于寻求分析系统中各子系统（或因素）之间的数值关系，但不适合分析整体性的、不可分的系统。事故树分析法应用较为普遍，但它仅适合描述规模不大的静态系统，无法分析动态系统。Petri网描述问题的能力很强，且非常适合分析系统变化的动态行为。考虑Petri网所具有的优点及列车在区间运行的特点，本文采用Petri网对铁路列车在区间运行安全状况进行动态分析。

1 Petri网的基本理论

1.1 Pe tri网定义 Petri网为一个有向图，可以用一个六元组来表示。即

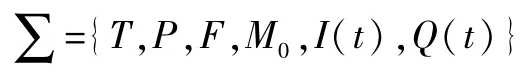
式中：T=｛t1，t2，…tn｝为变迁集，ti为一个事件或系统行为，i=1，2，…n；

P=｛P1，P2，…Pl｝为库所集，Pi为事件发生的状态或结果，且能容纳一个或多个托肯，i=1，2，…l；

F是连接变迁与库所，以及库所与变迁之间的有向弧集合，满足P∩T=Φ，P∪T≠Φ，F⊆（P×T）∪（T×P）；

M0∶P→N0为系统的初始标识，可以用 M=｛m1，m2，…，ml｝来描述系统在某个时刻的状态，其中，mi表示库所Pi中所含有托肯的数目（托肯用圆点来表示，它们在库所中的动态变化反应了系统的不同状态）；

I（t）=｛P│（p，t）∈A｝以及 Q（t）=｛p│（t，p）∈A｝分别代表变迁的输入库所集和输出库所集。

库所与变迁的变化状态，如图1所示。

图1 库所与变迁的变化状态

图中（a）反映了变化前的状态，库所 P1，P2分别有2个和1个托肯。当T1变迁被触发后，P1，P2各失去1个托肯，将P3得到1个托肯，变化后的状态如图中（b）所示。可见，当变迁被触发，输入库所将失去托肯而输出库所将得到托肯。

1.2 Pe tri网性质

1.2.1 定理一 对于一个有n个库所，m个变迁的Petri网，其关联矩阵定义为一个n×m的整数矩阵，它的元素定义为：A（i，j）=O（pi，tj）-I（Pi，tj）。根据Petri网的变迁规则，对于存在的一组变迁 t0，t1，t2…，tn，使得标识Mn从M0可达，则得到以下状态方程：

1.2.2 定理二 若非负整数向量X（n×1）满足：ATX=0，则X称是Petri网的一个S-不变量：若非负整数向量Y（m×1）满足 AY=0，则称 Y是 Petri网的一个 T-不变量。在关联矩阵和S-不变量的基础上，可以分析petrel网的结构性能：

2）只要存在一个正实数向量X（n×1），使得ATX=0，则Petri网是结构上守恒的。

S-不变量则反映Petri网的互斥行为，可用于Petri网的死锁分析和进行错误检测等，而T-变量能够反映Petri网的周期性，循环性等性能。

一般的，一个合理的Petri网系统应满足上述2个定理。此外，还应具有活性、有界性、可达性、安全性等4个重要性质。

2 Petri网模型的建立及分析

2.1 Pe tri网模型的构建 由于列车区间运行中可能出现的各种状态，它可以用Petri网模型来描述该系统变化的动态过程[7，8]。我们根据 Petri网的原理建立了图2所示的列车区间运行Petri网模型，该模型中包含有14个变迁和8个库所。

图2 列车区间运行Petri网模型

当列车从车站出发，进入区间运行（P1）后，可能会遇到7种不同的情况，分别是轨道电路故障（T1）、应答器故障（T2）、列车超速防护系统（ATP）故障（T3）、通过色灯信号机故障（T4）、线路限速行驶（T5）、ATP出现禁止信号（T6）以及列车追踪运行（T7）。

对于这些不同的状况，列车分别处于相应的行车状态，分别是目视行车状态（P2）、列车处于部分监控状态（P3）、列车处于按调度命令行车状态（P4）、列车等待，判断信号（P5）、列车已通过限速区段（P6）、列车处于隔离模式状态（P7）、列车处于运行判定状态（P8）。

接着对列车司机各种状态进行判断后，采取相应的行车速度前行。各判定状态相对应的分别是以最高20 km/h运行（T8）、以最高120 km/h运行（T9）、列车按调度命令运行（T10）、等待超过2m in则以不超过20 km/h速度运行（T11）、列车按规定时速运行（T12）、目视行车下最高20 km/h运行（T13）。

在以上7种（T7到T13）列车运行状态时，列车处于运行判定状态（P8），列车向前运行进入到下一个区间（T14），继而列车处于区间运行状态（P1），形成一个循环系统。

例如，列车进入某一区间时，P1内有1个托肯。此时可以被激发的变迁有7个，分别为T1，T2，T3，T4，T5，T6及T7。当T7被激发时，列车进入追踪运行状态，使得P8得到1个托肯，此时列车处于运行判定状态，继而激发变迁T14，列车进入下一个区间运行，P1中将得到1个托肯，列车向前方区段运行。

2.2 模型合理性分析 下面将运用上述Petri网的2个重要定理对所建立的Petri网模型进行合理性分析。首先建立关联矩阵，而后求得S-不变量和T-不变量，以此对所建立模型的数学特性进行分析[9]。

2.2.1 S-不变量的计算 对图2所示的Petri网模型，依据“1.2.1”中的（1）式建立关联矩阵，并求解S-不变量。可得关联矩阵如下：

由式子ATX=0，得到S-不变量：

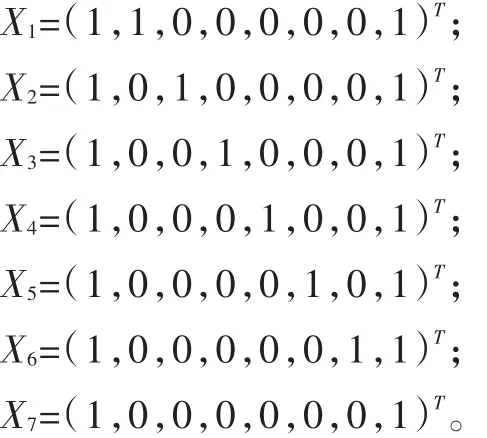
其中各不变量对应的库所（托肯的流动范围）为：

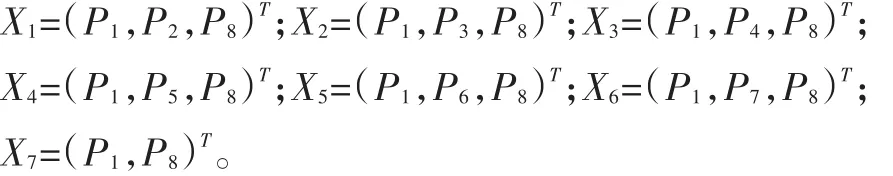
由此可知，在图2中托肯可能走的路线为：1）P1→P2→P8；2）P1→P3→P8；3）P1→P4→P8；4）P1→P5→P8；5）P1→P6→P8；6）P1→P7→P8；7）P1→P8。

2.2.2 T-不变量的计算 对图2所示的铁路列车区间运行Petri网模型建立的关联矩阵，求解T-不变量。

由式子AY=0，可得T-不变量：

由以上分析可知，系统的变迁可以通过7条不同的路径被激发，从而使系统不断的操作循环。这7条路径分别为：

2.2.3 合理性分析 由对S-不变量和T-不变量所进行的计算分析可知：

1）库所中托肯的流动过程反映了列车区间运行过程的Petri网模型具有活性、有界性和可达性，Petri网模型系统是安全的。

2）每一条径路Y均可以从初始变迁被激发，接着激发相应的库所导致后续变迁被激发，一定可以到原来的位置，从而构成一个完整循环过程。

由此看出，所建立的模型满足Petri网基本性质，并能够很好的反映列车在区间运行时可能遇到的各种情况以及采取的相应的行车方式，可以通过分析实际案例找出事故发生的环节（库所和变迁）。

3 Petri网模型的应用

3.1 事故预防 在图2所示的列车区间运行的Petri网模型中，系统状态的变化是通过托肯在库所之间的流动，激发相应的变迁所导致的。托肯从每个库所流动到下一个库所必须通过激发相应的变迁才能实现。库所P1为列车进入闭塞分区运行，具有2个托肯，司机托肯和车载系统托肯。其中，车载系统托肯用2种状态表示：正常以及故障，同样地，司机托肯也用2种状态表示：正确操作以及未正确操作。

下面以 P1→T1→P2→T8→P8→T14→P1这一循环路径为例说明库所变迁以及托肯是如何反应实际情况的。如果P1中托肯为司机正确操作和车载正常，此时若出现轨道电路故障（T1），则P1中托肯经过激发T1流动到P2中，即列车处于目视行车状态；如果此时P2中托肯无变化，则可以激发T8（即列车以最高20 km/h运行），列车继续向前运行，此时托肯流动到P8中，列车处于运行判定状态；同样司机托肯和车载正常时，可以激发T14，即列车进入下一区间运行，进而列车进入前方区段的运行状态（P1）。在上述过程中，如果库所中的任一托肯发生变化（即司机未正确操作或者车载故障），则相应的变迁不会被激发，从而造成循环中断。

该列车区间运行的Petri网模型中有7个环路，每一个环路中都可以使列车安全的行驶到下一区间。在车载和司机托肯都正确的情况下，出现（T1到T7）运行状况，只要托肯不发生变化以及各相应环路中的库所状态保持正确，列车都能够安全的驶到下一区间。但是当环路中某处中断，也就是环路中相衔接的库所和变迁的状态不能够发生变化时，就会出现事故。我们可以通过有效地掌握各个环路中的库所和变迁的托肯流动情况，使托肯能够顺利的在库所和变迁中流动，进而达到预防事故发生的目的。

3.2 事故案例分析

3.2.1 事故案例 这里我们用此模型对一实际案例进行分析。该案例为1列旅客列车冲突重大事故[10]。某铁路局某机务段BJ型2101号机车牵引的xxx次旅客列车（编组 18辆，总重932 t，计长39.6），行至XX线XX局管内B站至A站间K608+950处，与前行的YYYY次货物列车追尾冲突。造成机车中破1台，客车报废3辆、小破15辆，货车报废1辆、大破2辆；死亡40人（其中乘务员32人，旅客8人）、重伤9人（其中乘务员7人，旅客2人）、轻伤39人（其中乘务员4人，旅客35人）；直接经济损失130万元；中断京广下行正线行车11 h 15m in。

事故发生原因：xxx次机车班组在接受XXX号调度命令后，未经确认错误理解内容，将A站至B站间按特定闭塞法行车误认为C站至B站间，且擅自关闭机车信号和自停装置，严重违章。运行中精神不集中，遇黄灯不减速、红灯不停车，直至看到前方有车时，已经错过制动时机。

3.2.2 Petri网环路分析 案例中的情况可以采用图2所示模型进行分析。从发生原因可知，事故激发的路径为图3所示的环路。

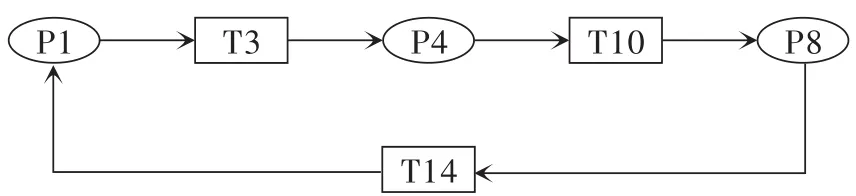
图3 案例事故里中断的Petri网环路

在案例中，司机擅自关闭机车信号和自停装置（也就是车载系统），即意味着P1的司机托肯中的未正确操作状态以及车载系统托肯中的未正确操作状态，使得变迁T3被激发，2个托肯转移到库所P4中；此时，列车处于按调度命令行车状态，但是由于列车司机错误理解调度命令，没有按照调度命令的正确内容执行作业，即后面的变迁T10没有被激发，托肯没有进入到库所P8中，循环中断，从而造成事故的发生。可见，出现事故主要是因为在P4和T10托肯的流动中断了。通过上述分析，可知主要因素有如下几点：

1）列车司机错误理解调度命令，没有按照调度命令行车。

2）司机擅自关闭车载信号，这就使得司机必须通过瞭望地面信号来保障行车安全，很容易误看地面信号的指示，造成下一步的操作失误。

3）列车司机遇到信号机没有按照信号显示的信息方式行车。

4）列车司机关闭自停系统，使得列车刹车的准确时机得不到保障，以至于依靠人工辨别停车时机。

根据以上所分析的原因，有关部门可依此采取相关措施，以减少此类列车区间运行事故的发生。

4 结束语

安全是铁路行车作业的重要质量保证。本文通过对列车在区间运行过程的分析，构建了列车区间运行安全的Petri网模型，并运用Petri网的T-不变量和S-不变量性质验证该模型的正确性，同时对实际案例进行分析，找出影响的主要因素。结论表明，所建的列车区间运行安全的Petri网模型是有效的、合理的，进一步为铁路行车安全的分析提供了一个有效方法，使管理者能有效地制定对策、控制危险因素，从而达到安全生产的目的。

[1]王广，韩莉.用灰色关联分析法研究矿区铁路运输事故特性[J].铁道运输与经济.1998（10）.

[2]栾夺.铁路调车挤岔事故的分析、预防与控制[J].铁道运输与经济.2002.24（3）.

[3]李振烈.杨霞芳.应用事故树分析法分析列车冒进信号机事故[J].铁道运输与经济.2002.24（4）.

[4]郑伟.基于随机 Petri网的平交道口建模及事故率分析[J].中国安全科学学报.2009.19（2）.

[5]李珊珊.郑中义.基于 Petri网的船舶碰撞事故致因[J].大连海事大学学报 2010.11（4）.

[6]牟海波，俞建宁.基于故障Petri网的车务段接发列车事故建模分析[J].铁道运营技术.2010.1

[7]袁崇义.Petri网原理[M].北京：电子工业出版社，2005.

[8]江志斌.Petri网及其在制造系统建模与控制中的应用[M].北京：机械工业出版社，2004.

[9]张玉洁.基于Petri网的铁路集装箱运输流程建模与优化研究[J].北京交通大学.2007.

[10]铁道部.铁路行车事故案例选编[M].北京：中国铁道出版社，1999.