高墩大跨连续箱梁铁路桥动力性能试验研究

黄胜前，杨永清

(西南交通大学土木工程学院，成都 610031)

大跨度连续箱梁是山区铁路桥梁的主要结构形式之一。为了了解此类桥梁的动力性能，通过理论计算与动载试验相结合的方法，分析了宜万铁路双流大桥主桥的自振特性及车桥耦合动力响应。据此，可以判断桥梁结构的刚度和强度等是否达到设计要求，列车运行的安全性和平稳性是否满足规范要求，同时也为桥梁的运营管理积累资料，为同类桥梁结构设计提供依据。

宜万铁路双流大桥主桥为变截面预应力混凝土连续箱梁，采用纵、竖向预应力体系，悬臂浇筑法施工，跨径组合为(60+108+60)m。箱梁为单箱单室直腹板截面，顶板宽6.5 m，底板宽5.1 m，外翼缘板悬臂长0.7 m;顶板厚0.35 m，腹板厚为0.35～0.7 m，底板厚0.4～0.96 m，中支点处加厚至1.1 m;中支点处梁高7.5 m，梁端和跨中处4.0 m，按半径395.5 m圆曲线变化。分别在中支点、梁端、跨中处设置厚2 m、1.3 m和0.6 m的横隔板。梁体混凝土为C55，纵向预应力筋为12－7φ5 mm钢绞线，竖向预应力筋为φ25 mm高强精轧螺纹粗钢筋，采用TPZ-Ⅰ型盆式橡胶支座。下部结构为桩基础，最大墩高84 m［1］。

1 车桥耦合振动分析［2-8］

列车通过桥梁时会导致桥梁结构发生振动，同时桥梁也会对车体产生反作用力，引起车辆振动，称为车桥耦合振动。车桥耦合振动分析需分别建立车辆动力分析模型和桥梁动力分析模型，通过轮轨的几何相容条件和相互作用力平衡条件将两者联系起来，组成车桥耦合振动系统。随着列车在桥梁上运行，系统是时变的;轮轨之间既有非线性几何约束关系，又有非线性的接触蠕滑关系;车桥耦合系统是自激系统，主要的激励源“轨道不平顺”具有随机性。

列车机车与车辆由车体、转向架和轮对等主要部分组成。轮对和转向架之间由包括线性弹簧和粘性阻尼器的一系悬挂系统分别在纵向、竖向、横向连接，转向架和车体之间由另一组线性弹簧和粘性阻尼器组成的二系悬挂系统分别在纵向、竖向、横向连接。假定:车体、转向架和轮对均为对称刚体，做微振动;不计机车与车辆纵向振动的影响;桥上线路为直线，不考虑机车与车辆之间的相互作用;不计转向架扭曲变形;不计轮对与转向架之间的横向间隙对系统响应的影响;不计悬挂元件(弹簧和阻尼)的非线性特性。车体和每个转向架各有5个自由度(浮沉、横摆、侧滚、摇头、点头)，每个轮对考虑4个自由度(浮沉、横摆、侧滚、摇头)。

桥梁动力分析模型可运用有限元方法建立，主梁、桥墩均采用空间梁单元，每个节点考虑3个线位移和3个转角位移，共6个自由度。桥面构造和附属设施的质量均匀分配到主梁单元中。将各个单元在整体坐标系下的质量、刚度和阻尼矩阵分布组集，形成整个结构的质量、刚度和阻尼矩阵，得到桥梁振动方程

式中，Mb、Cb、Kb分别为桥梁的质量、瑞利阻尼及刚度;Fb为作用在桥梁上的节点力;Xb、˙Xb、¨Xb分别为桥梁的位移、速度和加速度。

轮轨接触力考虑竖向轮轨力和横向轮轨力。竖向轮轨力为轮对轴重加上轮对惯性力及通过与轮对连接的竖向弹簧和阻尼器传递的弹簧力和阻尼力;横向轮轨力则与轮对在钢轨上的蠕滑力有关。可根据赫兹接触理论和Kalker滚动接触蠕滑理论分别建立竖向、横向轮轨接触力方程。

根据轮轨接触点的几何相容条件和相互作用力平衡条件，可得车桥耦合振动微分方程

式中，M、C、K分别为质量、阻尼及刚度矩阵;X为位移矢量;F为作用力;下标B、T分别表示桥梁和车辆。

将轨道不平顺作为车桥系统的外部激励源，考虑线路中心线竖向高程偏差、横向位置偏差、左右轨距偏差、左右轨竖向高程的歪扭4种情况。

2 实桥动载试验方法

结合宜万铁路双流大桥主桥(60+108+60)m连续箱梁的结构特点，选取边跨跨中附近截面、7号墩墩顶附近截面和中跨跨中附近截面布置动力测试测点，如图1所示。在B－B/C－C、D－D截面顶、底板各对称布置2个动应变测点，每个截面共布置4个;在截面DD上下游侧对称布置1个动挠度测点，共2个。沿桥跨方向等间距布置17个自振测点，采用脉动法测定桥跨结构的自振频率、振型及阻尼比。行车试验和制动试验采用单列货车进行，货车编组为1HXD1C+25C64K/C70H/C70+1HXD1C。行车试验按5 km/h的速度进行标定车速试验后，依次按 20、40、60、80 km/h的速度进行;制动试验按40 km/h的速度运行并在指定部位制动。主要测试内容包括:B－B/C－C、DD截面动应变，D－D截面动挠度及横向和竖向振幅、加速度，7号墩墩顶横向和纵向振幅、加速度，6号墩活动支座的横向和纵向位移。

图1 双流大桥主桥动载试验测点布置示意(单位:m)

3 自振特性分析

为了分析双流大桥主桥的动力特性，运用有限元方法建立了动力分析模型，如图2所示。

双流大桥主桥自振特性的计算及实测结果详见表1。

双流大桥主桥的自振频率、振型及阻尼比采用脉动法测定。横向基频的计算和实测结果分别为0.489 Hz和0.684 Hz，竖向基频的计算和实测结果分别为1.102 Hz和1.660 Hz。计算值低于实测值，主要是由于计算中边界约束条件的模拟存在偏差造成的，在计算中支座均按理想的固定铰或可移动铰模拟，忽略了支座本身和桥面轨道系统的扭转约束和纵向约束。参照《铁路桥梁检定规范》［9］中简支梁的有关规定，可判断本桥桥跨结构横向刚度较好。桥跨结构的一阶横弯、一阶竖弯的阻尼比分别为0.024和0.068。梁体横向一阶、竖向一阶振型曲线的计算与实测结果基本吻合，反映了桥跨结构竖、横向的振型特征，如图3所示。

表1 双流大桥主桥自振特性

图2 双流大桥主桥动力分析有限元模型

图3 双流大桥主桥一阶振型计算及实测结果

4 桥梁动力响应

4.1 动应变及动力系数

试验列车以不同的速度通过桥梁，测得双流大桥主桥7号墩墩顶(B－B)截面和中跨跨中(D－D)截面应变时程曲线如图4所示。

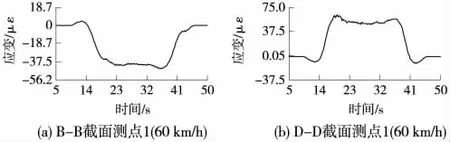
图4 双流大桥主桥典型应变时程曲线

根据实测应变时程曲线分析得到各测试截面动力系数见表2。

从测试结果可以看出，7号墩墩顶(B－B)截面各测点应变动力系数介于1.018～1.057，中跨跨中(DD)截面各测点应变动力系数介于1.003～1.040。实测动应变曲线相对于影响线有轻微的波动现象，实测应力动力系数相对较小，最大值为1.057，表明试验车辆对桥跨结构的动力作用并不明显。

表2 双流大桥主桥墩顶及跨中截面动力系数

4.2 振幅及加速度

表3列出了试验列车以不同速度通过桥梁时7号墩墩顶(B－B)和中跨跨中(D－D)的振幅值。在各动载试验工况下，7号墩墩顶最大纵向、横向振幅分别为0.33、0.04 mm，中跨跨中最大竖向、横向振幅分别为0.70、0.75 mm，7号墩墩顶横向振幅、中跨跨中横向振幅均小于《铁路桥梁检定规范》通常值。

表3 双流大桥主桥墩顶及中跨跨中振幅 mm

表4列出了试验列车以不同速度通过桥梁时7号墩墩顶(B－B)和中跨跨中(D－D)的加速度值。在各动载试验工况下，7号墩墩顶最大纵向、横向加速度分别为0.10、0.32 m/s2，中跨跨中最大竖向、横向加速度分别为0.20、0.67 m/s2，横向加速度满足《铁路桥梁检定规范》横向振动加速度不应超过1.4 m/s2的规定，表明桥跨结构横向动力性能良好。

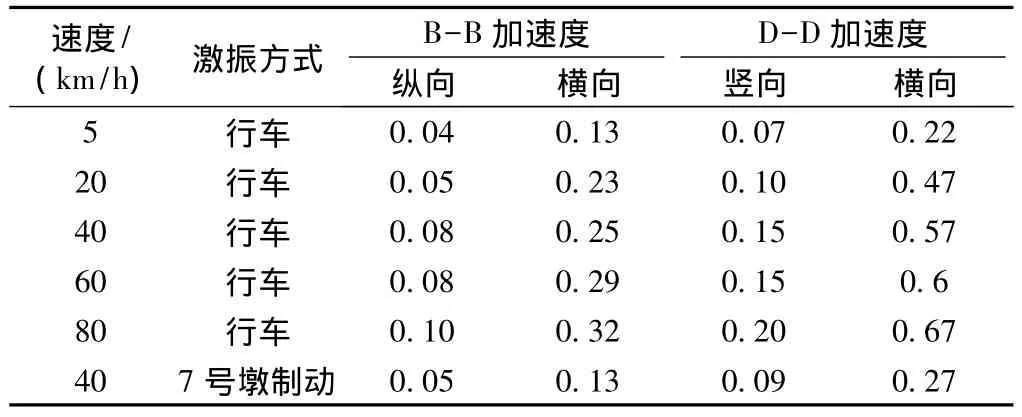
表4 双流大桥主桥墩顶及中跨跨中加速度 m/s2

4.3 动挠度及支座位移

双流大桥主桥中跨跨中动挠度实测结果见表5，动挠度时程曲线如图5所示。在各动载试验工况下，主梁中跨跨中附近动挠度介于42.0～43.7 mm，动挠度时程曲线过渡较为圆顺，说明桥跨结构受到试验列车冲击较小。

双流大桥主桥6号墩处多向活动支座横向、纵向实测动位移测试结果见表5。动载试验货车作用下，实测支座横向位移最大值为0.64 mm，满足《新建时速200公里客货共线铁路设计暂行规定》［10］支座横向位移不大于±1 mm要求。

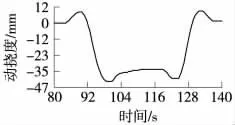
图5 双流大桥主桥典型动挠度时程曲线

表5 双流大桥主桥跨中动挠度及6号墩支座位移

5 机车与车辆动力响应

5.1 安全性指标

车桥耦合振动分析表明，机车与车辆的三项安全性指标，轮轴横向力、轮重减载率及脱轨系数分别满足《新建时速200公里客货共线铁路设计暂行规定》规定的80 kN、0.8和0.6的限值，详细结果见表6。可以看出，机车与车辆的轮轴横向力、轮重减载率及脱轨系数等安全性指标基本上随行车速度的增大而增大。对于客车，行车速度为160 km/h时，各项安全指标取得最大值;对于货车，行车速度为90 km/h时，各项安全指标取得最大值。

表6 机车与车辆过桥的安全性指标

5.2 加速度及平稳性指标

列车横向、竖向加速度及平稳性指标的计算结果见表7。可以看出，机车与车辆横向、竖向加速度随速度的增大而增大，客车、货车的最大横向、竖向加速度均满足规范要求。机车与车辆横向、竖向平稳性指标也随速度的增大而增大，依据《铁道机车动力学性能试验鉴定方法及评定标准》［12］、《铁道车辆动力学性能评定和试验鉴定规范》［13］，在计算速度范围内，客车、货车机车与车辆平稳性等级均达到“优良”或者“良好”。

表7 机车与车辆过桥的加速度及平稳性指标

6 结论

(1)宜万铁路双流大桥主桥桥跨结构横向、竖向基频的实测结果分别为0.684 Hz和1.660 Hz，略高于计算值，桥跨结构横向刚度较好。

(2)在各速度行车和制动试验工况下，实测动应变及动力系数均较小，动力系数最大值仅1.06，说明本桥结构强度和刚度较好，行车和制动对桥跨结构的动力作用并不明显。

(3)在各速度行车和制动试验工况下，7号墩墩顶及中跨跨中振幅及加速度均满足《铁路桥梁检定规范》要求，本桥结构刚度和动力性能良好。

(4)在各速度行车试验工况下，中跨跨中动挠度介于42.0～43.7 mm，动挠度时程曲线过渡较圆顺，说明桥跨结构受到试验列车冲击作用较小。

(5)实测支座最大横向位移为 0.64 mm，小于±1 mm，满足《新建时速200公里客货共线铁路设计暂行规定》要求。

(6)车桥耦合振动分析表明，机车与车辆动力响应满足规范要求，安全性、平稳性及舒适度均较好。

［1］杨宏.宜万铁路双流特大桥连续梁施工技术［J］.铁道标准设计，2007(3):61-63.

［2］王彬力，蒲黔辉，白光亮.新型U型梁车桥耦合环境振动实测与分析［J］.地震工程与工程振动，2012，32(1):78-85.

［3］卫星，李小珍，李俊，强士中.铁路大跨连续刚构桥动力性能研究［J］.振动与冲击，2009，28(11):118-121.

［4］翟婉明.车辆-轨道耦合动力学［M］.北京:中国铁道出版社，2002.

［5］葛玉梅.斜拉桥在考虑风效应时的车－桥耦合振动［D］.成都:西南交通大学，2001.

［6］施洲，夏招广，葛玉梅.钢管混凝土劲性骨架提篮拱桥动力试验及车桥耦合振动分析［J］.铁道学报，2006，28(4):95-101.

［7］施洲，夏招广，葛玉梅.高墩大跨连续梁铁路桥动力试验［J］.西南交通大学学报，2006，41(3):349-354.

［8］凌知民，曹雪琴，项海帆.铁路高墩连续梁车桥耦合动力响应分析［J］.铁道学报，2002，24(5):98-102.

［9］张楠，张田，杜宪亭，杜士杰.客运专线连续梁拱桥细部应力及车桥动力分析［J］.铁道标准设计，2011(S):75-79.

［10］铁运函［2004］120号 铁路桥梁检定规范［S］.北京:中国铁道出版社，2004.

［11］铁建设函［2005］285号 新建时速200公里客货共线铁路设计暂行规定［S］.北京:中国铁道出版社，2005.

［12］TB/T 2360—1993 铁道机车动力学性能试验鉴定方法及评定标准［S］.北京:中国铁道出版社，1993.

［13］GB/T 5599—1985 铁道车辆动力学性能评定和试验鉴定规范［S］.北京:中国标准出版社，1985.