既有铁路曲线整正计算中的计划正矢计算方法的研究

刘永孝，刘学毅，李 斌，代 丰

(1.兰州交通大学土木工程学院，兰州 730070;2.西南交通大学土木工程学院，成都 610031)

计划正矢的计算实现程序化是铁路曲线整正的一个重点和难点［1-3］。在传统的计划正矢的计算中，一般采用的是人工判断的方法，通过判断测点所处曲线的位置采用不同的公式，计算出相应的计划正矢。如果要实现铁路曲线整正计算的程序化，必须要解决计划正矢的程序化，这就需要推导出曲线在不同测点处计划正矢的公式，自动判断测点所处的位置及采用相应的公式。

铁路曲线整正计算中通常采用的方法是偏角法、坐标法、绳正法，在传统的曲线整正计算中，通常情况下只是采用其中的一种方法来进行计算整正，很少将它们联系起来考虑。一般在绳正法整正曲线时，需要考虑计划正矢，而利用其他2种方法计算时，很少考虑曲线的计划正矢，如果能够推导出坐标法和偏角法中计划正矢的计算公式，这样既可以拓展计划正矢的计算方法，又可以在坐标法和偏角法中通过分析其计划正矢和拨后正矢来判断曲线的圆顺度，同时通过计划正矢作为结合点，将3种方法融汇贯通。

将3种方法分别计算各自的计划正矢并进行比较分析，坐标法计算的计划正矢的结果是精确的，绳正法和偏角法计算的计划正矢有一定的误差，将它们和坐标法计算结果进行对比分析，可判断出绳正法和偏角法误差的大小及规律。进而可分析出其引起的计划渐伸线的误差，并可分析出其拨距计算的一些误差的原因及改进的方法。同时利用这些公式，现场可灵活地计算出各测点的计划正矢。通过这些计算公式可计算出各种方法的拨后正矢。

1 计划正矢计算的理论分析

1.1 绳正法计算各测点的计划正矢

利用绳正法计算计划正矢时，首先要知道曲线的桩点里程，然后找到计算点的位置，根据其处在曲线不同的位置采用相应的公式进行计算。为此，可把曲线分成5段(即前直线，前缓和曲线上，圆曲线，后缓和曲线上，后直线上)，当计算点的前一测点和后一测点落在同一性质的曲线上，如图1中的1、4、7、10、13点，处在相应的5段曲线上，分别采用式(1)，式(4)，式(7)、式(10)、式(13)的公式进行计算。针对曲线4个桩点(ZH，HY，YH，HZ)附近的8个点，由于计算点的前一个测点和后一个测点落在不同性质的曲线段上，如图1 中的 2、3、5、6、8、9、11、12 点，计算时分别采用相对应式(2)、式(3)、式(5)、式(6)、式(8)、式(9)、式(11)、式(12)的公式进行计算。这个公式即可计算出曲线任意布点的情况下整条曲线的计划正矢，这样即可实现计算计划正矢的公式化。其测点布置如图1所示，计算公式见式(1)～式(13)。

式中 xi——计算点的测点号;

fi——各计算点对应的计划正矢;

xZH，xHY，xYH，xHZ——分别代表直缓、缓圆、圆缓、缓直点的桩点号数;

fy——圆曲线计划正矢;fy=(mm);

fd——曲线正矢递变率;fd=，m0为缓和曲线段数。

利用以上公式可计算出曲线上所有点的计划正矢。

1.2 利用坐标法计算各测点的计划正矢

已知曲线主要桩点的里程，可根据各桩点的位置计算出各计算点的设计坐标，再根据各测点的设计坐标计算出各点的计划正矢。

1.2.1 计算各测点的坐标

A、B、C分别处在第一缓和曲线、圆曲线、第二缓和曲线上的点，坐标系的建立如图2所示，以ZH点为坐标原点，ZH点以前的直线段为x轴，垂直于x轴且指向圆心那侧为y轴，此坐标称为第一坐标系，计算前直线、第一缓和曲线和圆曲线上的测点的坐标时，可直接在此坐标下进行计算。其坐标计算公式分别采用式(14)、式(15)、式(16)。计算第二缓和曲线和后直线上的测点时，以HZ点为坐标原点，HZ点以后的直线为x'轴，垂直于x'且指向圆心那侧为y'轴，先计算在此坐标系下的它们坐标公式，分别采用式(17)、式(19)。然后通过坐标转换公式把它们转化在第一坐标系下的公式，其转化公式分别采用式(18)、式(19)。在第一坐标系下，再利用公式［4-6］(式(21))计算出各计算点的计划正矢。

图2 计算各测点设计坐标示意

式中 ki——计算点桩点里程

A，B，C——分是处于第一缓和曲线、圆曲线、第二缓和曲线上的点;

ZH，HY，YH，HZ——直缓、缓圆、圆缓、缓直点的桩点里程;

xHZ，yHZ——HZ 点的坐标;xHZ=T(1+cos α)，yhz=T tanα，T为切线长;

m——曲线内移距，m=l0

l0——缓和曲线长度;

α——曲线转角。

1.2.2 计算各点的计划正矢

用式(14)～式(17)计算出各点的设计坐标，已知扣点的计算坐标可计算出各点的计划正矢，其计算如图3所示。

图3 利用坐标法计算计划正矢示意

1.3 利用偏角法计算各测点的计划正矢公式

已知曲线的主要桩点位置，根据各计算点所处的位置，利用公式(式(22)～式(26))［7］先计算出各测点的计划渐伸线长度，然后利用公式(式27)计算出各测点的计划正矢。

(1)计算各点的渐伸线长度计算公式［8］，

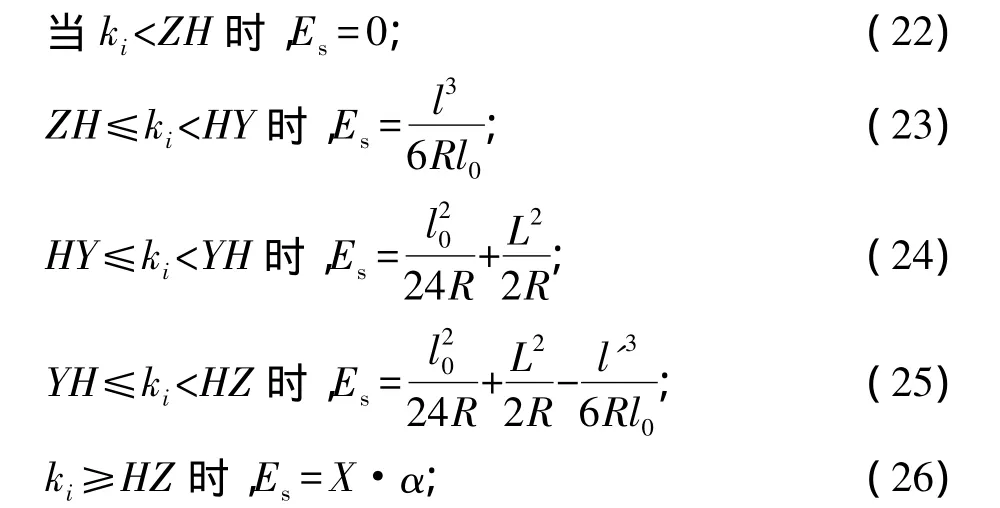
式中 Es——计算渐伸线长度;

l——计算点至ZH点的距离;

L——计算点至ZY点的距离;

l'——计算点至YH点的距离;

X——计算点至QZ点的距离。

(2)各测点的计划正矢为

(3)各测点的计划渐伸线长为

2 计划正矢及设计渐伸线误差理论分析

2.1 计划正矢误差分析

曲线上每隔10 m布置1个测点，同一曲线上采用同一布置测点的方法，分别利用上述3种方法的公式分别计算各曲线的计划正矢，运用现场大量曲线作为研究对象，通过编程计算，分析其计算结果可发现，利用偏角法和绳正法计算出的计划正矢是完全相同的，它们都是基于渐伸线原理计算的［9-12］。但是从计算难易程度来说，用偏角法计算计划正矢的方法要简单一些，故可通过偏角法来计算渐伸线的长度，通过计算出的渐伸线长度再计算出曲线计划正矢。这可为现场计算计划正矢提供一种简单而实用的方法。

通过对现场大量的曲线进行编程计算，把绳正法的计算结果和坐标法的计算作对比分析，将一些有代表特征的数据分析罗列于图4。从图4中可以看出绳正法的计划正矢误差都比较小，且随着曲线半径的减少，误差有所增加，当半径较小，转角较大时，其误差有所增加，但误差最大也不超过0.06 mm，并且误差最大点出现点HY、YH点附近，这是由于在HY、YH点是前后两种不同的线形的过渡段。由于实际应用中，对曲线计划正矢的设置、检查、曲线整正来说一般取到其整数位即可，故其误差对曲线计划正矢的设置没什么影响。对现场实际应用来说，利用坐标法和偏角法来计算计划正矢的方法较绳正法更为简单。

图4 绳正法计划正矢误差分析

2.2 设计渐伸线误差分析

从式(29)可以看出，拨距等于既有渐伸线长度减去计划渐伸线之差，而既有渐伸线长度在计算时不会产生误差，拨距的误差只会产生在计划渐伸线的计算中。利用坐标法计算出的计划正矢可计算出其计划渐伸线的长度，其值应该是精确的，将通过绳正法计算出的设计渐伸线长度同其作比较，可分析出其误差的大小及产生规律。

把绳正法、偏角法、坐标法计算的计划正矢利用公式(式28)可计算出它们计划渐伸线的长度，绳正法计算值和偏角法的计划渐伸线值理论上应该是相同的，通过对大量的曲线编程分析，也验证了这一结论。把绳正法计划渐伸线的长度同坐标法设计渐伸线长度进行对比，可分析出绳正法的计划渐伸线长度的误差及规律。通过对现场大量的曲线进行编程分析，选出与图4对应的几条曲线，它的分析结果如图5所示。从图5可知，其计划渐伸线的误差都是正的，随着测点的增加，其误差也越来越大。这说明利用绳正法计算出的渐伸线长度比坐标法计算出的大。在半径较大，曲线较短时，其误差较小，半径越小，曲线越长时，其误差越大，半径300 m，曲线长1200 m时其误差可达到200 mm，从图4可知，其计划正矢的误差很小，最大也不会超过0.06 mm。从中可知，即使较小的计划正矢误差也引起较大渐伸线误差，这是由渐伸线的计算特性决定的。如果将其误差理解为修正值的话，可以认为，只要满足一定的曲线规律，即使较小的计划正矢的修正值，也能修正较大的拨量。传统方法在调整拨量大小时，通过调整计划正矢使其拨量满足曲线整正的原则，并且使其拨量较小，在传统方法中，往往采用1 mm作为其修正值，通过以上分析可知，修正值取较小的值，如0.06 mm，也能得到较大的拨距修正值200 mm，从而能使拨距值变小。在高速铁路有砟轨道地段，它对曲线的圆顺度要求较高，如果计划正矢的修正值过大的话，对曲线的圆顺度的影响较大。通过上述分析可知，在采用修正计划正矢时不用取1 mm，可以取如0.1、0.2 mm等，计划正矢修正值取为0.1、0.2 mm时，它对曲线圆顺度几乎没有什么影响，在高速铁路有砟轨道地段采用此修正值既能取得较为满意的曲线整正结果，又能满足高速铁路对曲线圆顺度的要求。

3 结论

(1)偏角法和绳正法计算计划正矢的方法都是利用渐伸线原理计算的，它们的计算结果是完全相同。但利用偏角法计算计划正矢的公式简单，故在计算计划正矢时，可利用偏角法代替绳正法进行计划正矢的计算，这为现场计算计划正矢提供了一种新的方法。

图5 绳正法设计渐伸线误差分析

(2)坐标法计算出的计划正矢的结果是精确的，用偏角法和绳正法计算的计划正矢的结果和它相比，可得出它们的误差。通过分析可知:随着线路曲线半径的减小，误差也随着增大，虽然在半径较小时有一定的误差，但这些误差对曲线整正计算来说是可以忽略不计的。

(3)将绳正法和坐标法计算出的计划渐伸线长度进行比较分析发现，当半径较小，长度较长时，即使较小的计划正矢误差也能引起较大渐伸线长度误差。

(4)如果计划正矢的修正位置选择合适，即使较小的计划正矢的修正值也能修正较大的拨距。故在高速铁路有砟轨道地段，为了保证曲线圆顺度的要求，计划正矢的修正值可以取小一些，如修正值建议可采用0.1 mm或0.2 mm。

(5)利用这3种计算计划正矢的公式，可以为曲线整正计算中计划正矢的编程提供相应的理论依据。

［1］黎浩廉.对整正既有曲线的几个问题的探讨［J］.长沙铁道学院学报，1980(1):30-41.

［2］丁克良，刘成.GPSRTK技术在铁路既有线勘测中的应用［J］.中国铁道科学，2005，26(2):49-53.

［3］李红艳，陈治亚.铁路既有线曲线复测计算方法［J］.中国铁道科学，2009，30(2):18-21.

［4］刘永孝，刘学毅.铁路既有曲线整正计算中基于坐标法的渐伸线误差分析研究［J］.铁道学报，2012，34(4):82-87.

［5］李家稳，陈峰，张海燕，施仲衡.坐标法优化拨距计算方法的研究［J］.北京交通大学学报，2004，28(4):34-36.

［6］郝瀛.铁道工程［M］.北京:中国铁道出版社，2004.

［7］何恩祥，陆亚军.既有铁路曲线半径选择的目标函数及优化方法研究［J］.铁道学报，1990，12(3):92-96.

［8］刘永孝，张咏军.铁路既有曲线整正计算方法研究［J］.铁道建筑，2010，50(11):116-119.

［9］刘鑫，曾学贵.快速铁路既有曲线约束非线性最优化整正研究［J］.铁道学报，2003，25(3):101-103.

［10］何恩祥.渐伸线整正既有曲线误差及适用范围［J］.铁路航测，1992(2):33-37.

［11］郝赢.改建既有线平面时对传统误差分析［J］.铁道学报，1984，6(1):71-83.

［12］丁克良，刘大杰，周全基.既有铁路曲线整正平差算法［J］.测绘学报，2004，33(3):195-199.