汽车碰撞波形梁半刚性护栏的简化计算

许 颖，王 鹏

1)哈尔滨工业大学深圳研究生院，深圳518055;2)广州荣柏生建筑工程设计事务所，广州510170

汽车碰撞护栏是极为复杂的力学过程，属于运动结构的相互碰撞，与一般结构的受力过程完全不同.目前通用的接触—碰撞有限元分析算法可以解决这类问题，但由于其复杂性，即使用大型计算机也是一项昂贵耗时的工作［1-7］.对汽车碰撞护栏进行简化计算，可让护栏设计人员更清晰了解碰撞过程和碰撞机理，有利于护栏设计，且节约计算时间和成本，易于为一般工程设计人员接受.

本文以Newmark β法为基础［8-13］，研究了考虑汽车转动的简化模型(x和y方向平动与转动，共3个自由度).通过与LS-DYNA有限元模拟结果对比表明，考虑汽车转动的简化计算方法能较准确地对汽车碰撞半刚性护栏的过程进行时程分析.

1 Newmark β 法理论

在Newmark列式中，最终的速度和位移分别为

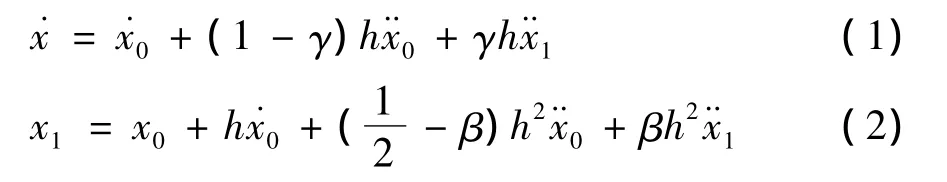
其中，h为计算时间步长.当β=1/6，γ=1/2时，

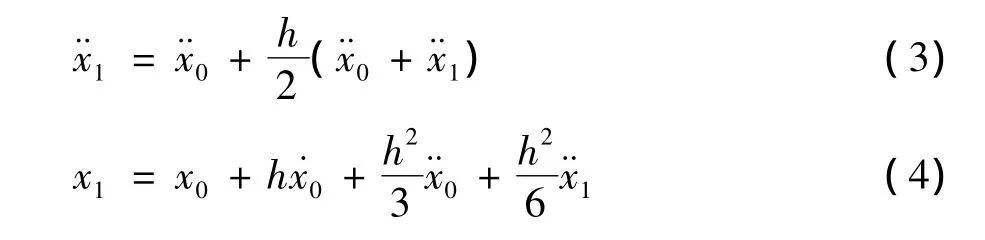
对非线性体系分析，物理特性假设仅在很短的时间或变形增量内保持常量.因此，可以按照下述方法根据增量方程来表示反应方程.

由力系平衡条件，可求得时刻t的增量平衡方程为

于是可得到增量等效静力平衡方程为

等效刚度和增量等效荷载的表达式为

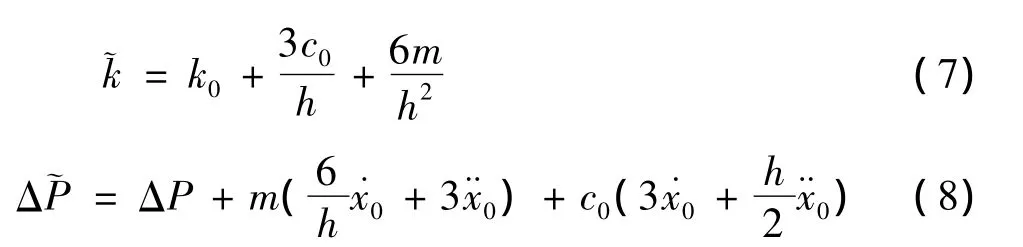
可得位移增量和速度增量分别为

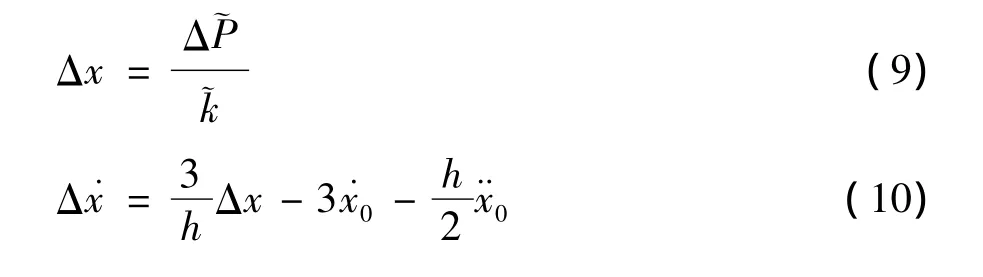
2 不考虑汽车转动的简化计算

2.1 基本假设

①汽车为集中质量块，波纹板、立柱和防阻块质量相对于汽车忽略不计;

②不考虑汽车轮胎与地面的摩擦;

③根据前人试验和有限元模拟结果，发现碰撞对护栏的影响跨度为4跨［14］.故简化计算模型截取4跨护栏，并在波形梁两端用固端约束;

④汽车与护栏沿纵向摩擦力不计［15］;

⑤冲击荷载作用下，忽略护栏阻尼.

2.2 计算简图

为与LS-DYNA模型保持一致，简化计算中，小客车质量m=1.5×103kg，碰撞速度v=100 km/h，碰撞角度θ=20°，初始碰撞点位置(z，x)=(24.5，0).图1为汽车碰撞护栏简化模型俯视图.

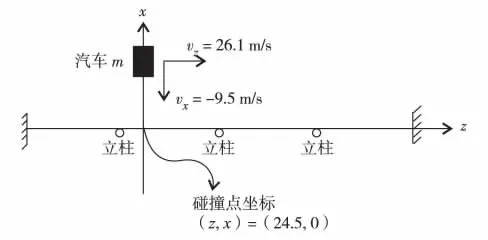
图1 汽车碰撞护栏简化模型俯视图Fig.1 Vertical view for simplified model of car crashing barrier process

按照基本假设条件，汽车碰撞护栏为平动自由度体系.把汽车的速度分解到x和z两个方向上分别考虑，汽车在z方向不受力，作匀速运动;在x方向受到护栏的作用，作减速运动.图2为汽车碰撞护栏在x方向的计算简图［16］.

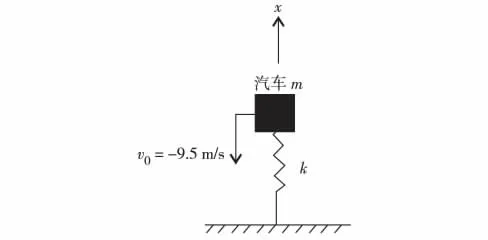
图2 不考虑汽车转动时的计算简图Fig.2 Calculation diagram without considering car rotating

2.3 简化计算过程

正方向规定:汽车的位移、速度和加速度的正方向为x轴正方向，汽车受到的惯性力、反弹力fs和阻尼力的正方向为x轴负方向.计算采用国际单位制.

应用Newmark β法，对汽车碰撞护栏作时程分析.汽车的初始位置为(z0，x0)=(24.5，0)，x方向初始速度为v0=-9.5 m/s，计算时间步长h=0.01 s.

等效刚度为

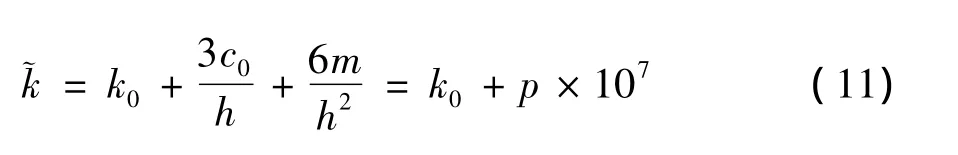
等效增量荷载为

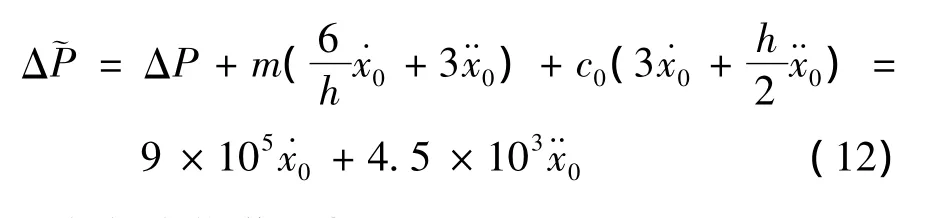
x方向位移增量为

速度增量为

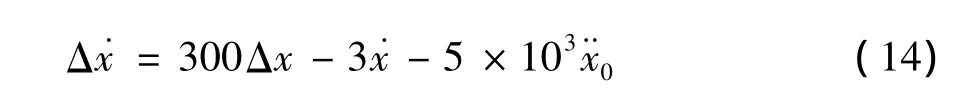
故唯一未知的量为非线性综合刚度k，它是由波形梁、防阻块、立柱和地基作为一个系统综合提供的.综合刚度k高度非线性，不仅随着x方向位移而改变，也随着z方向位移而改变.本研究由ANSYS［17］辅助计算.下面介绍由ANSYS辅助计算综合刚度k的方法，并引用前人公式验证其正确性.

为求综合刚度k，根据基本假设建立了ANSYS模型如图3.

加速度为

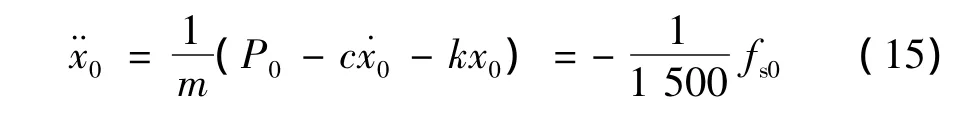
图3 辅助计算刚度的ANSYS模型Fig.3 ANSYS model of aided calculating stiffness

前面已假定汽车在z向匀速运动，考虑到计算时间和计算精度的要求，且时间步长的一般要求为h/T≤1/10(T为结构自振周期长度)，取计算时间步长h=0.01 s，综合刚度k为汽车运行到位置，n=0，1，2，…处的刚度.这些位置处的z值具体为24.5、24.761、25.022、25.283、25.544、25.805、….

设t=nh时，由Newmark法算出下一个时间步长内位移增量为Δx，即在t=(n+1)h时，z方向位置z=z0+Vznh，x方向位移增加Δx.

在时刻t=(n+1)h的综合刚度k求法是:在波形梁z处施加位移荷载，同时释放前面的位移荷载.由ANSYS可计算出波形梁z处的约束力，此约束力与fs1大小相等，方向相反.由此时刻fs1和前一步求得fs0，可外推求得此时刻的综合刚度k=(fs1-fs0)/Δx.非线性综合刚度在fs1＜fs0时可能为负值.得到综合刚度k后，即可算出不同时刻t时，z、x、、、Δx及Δ的值，结果见表1.

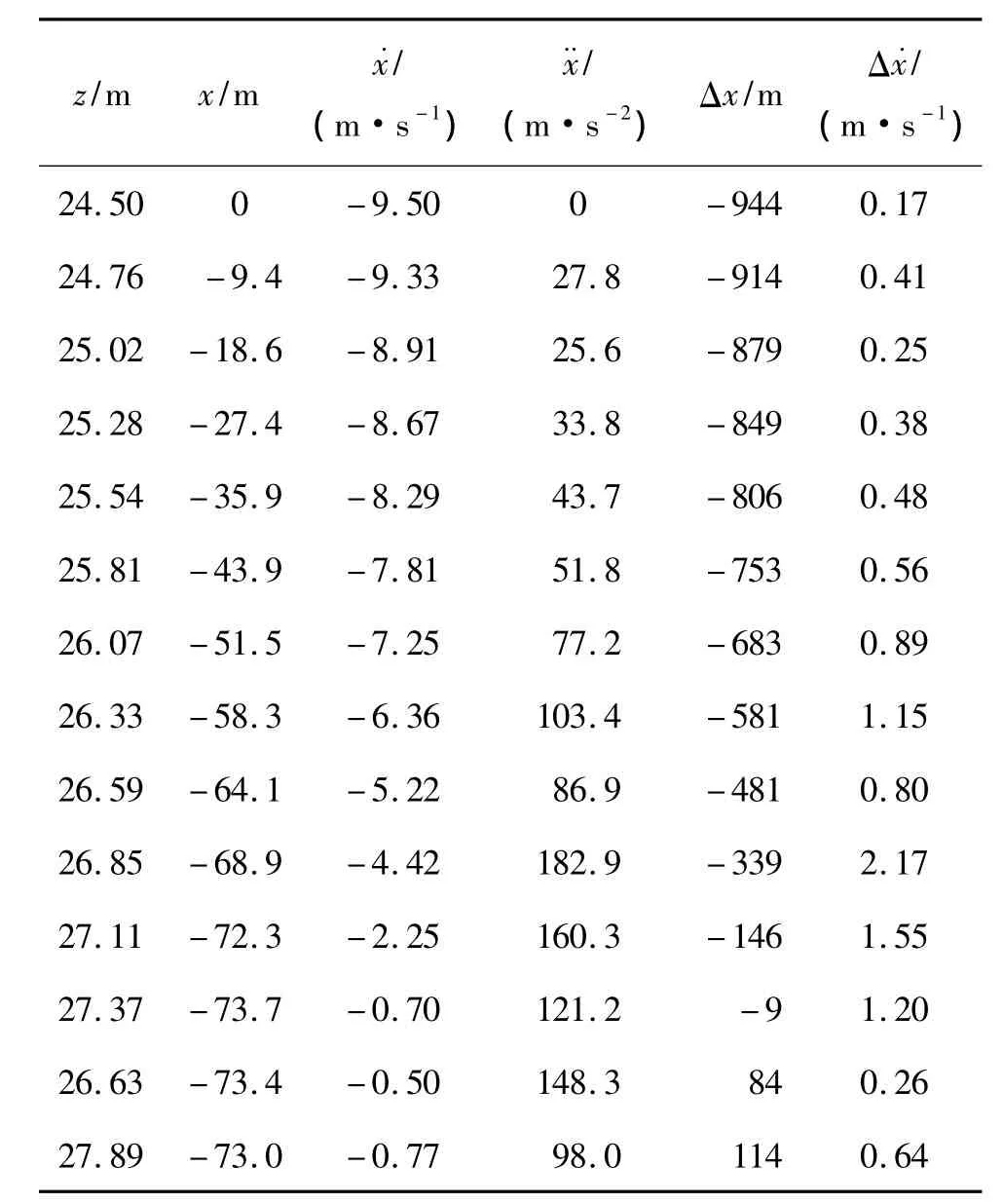
表1 不考虑转动汽车碰撞护栏时程分析Table1 Time domain analysis of car crashing barrier process without considering car rotating

2.4 与LS-DYNA模拟结果比较

用软件LS-DYNA对汽车碰撞护栏进行了模拟.其中，汽车长 4.637 m，宽 1.806 m，高 1.48 m.有限元模型坐标与简化计算坐标保持一致.简化计算中汽车质量块位移值x即为波形梁的动态变形量，其结果与有限元模拟对比如图4.

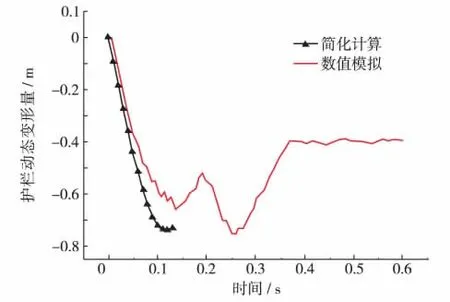
图4 护栏动态变形量比较Fig.4 Comparison of barrier dynamic deformation between simplified calculation and numerical simulation

从图4可知，简化计算值与模拟数值有一定差距，最大相差20%.这是由于简化计算只考虑x和y方向两个平动自由度，而没有考虑汽车转动自由度，在实际情况中，汽车是转动的［18］.

3 考虑汽车转动的简化计算

3.1 简化计算模型

考虑汽车转动与不考虑汽车转动的唯一不同，就是不把汽车当作质量块，而考虑其转动因素.其简化计算模型如图5.汽车的运动由汽车的平动和汽车绕质心的转动两部分组成.

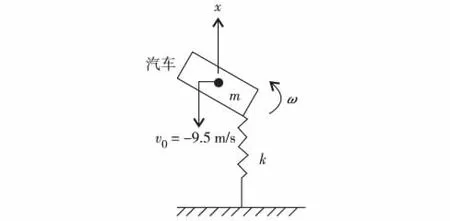
图5 考虑汽车转动时的计算模型Fig.5 Calculation diagram withconsidering car rotating

3.2 简化计算过程

计算过程中，考虑转动与不考虑转动的唯一不同之处，是护栏反弹力fs=kx中x的取值.不考虑转动时，x值为质量块质心位置处的x向位移值;考虑转动时，x值为汽车前角与护栏碰撞点处的位移值.考虑转动时，汽车前角碰撞点处的位移与汽车质心处的位移关系见图6.在图6中，B为汽车质心，A为汽车前角与护栏碰撞点，汽车转动的角速度以逆时针为正方向.在初始时刻，初始碰撞点A的坐标(z，x)=(24.5，0)，R为汽车质心B到前角点A的距离，φ为AB与汽车轴线的夹角，θ为x轴与汽车轴线的夹角，全部采用国际单位制.汽车长4.64 m，宽 1.81 m，φ =0.371°，初始时刻 θ=1.222°.根据几何关系可得 R==2.188 m，∠CAB=(θ-φ)rad.所以汽车质心和前角点的关系为xB-xA==Rcos(θ-φ).

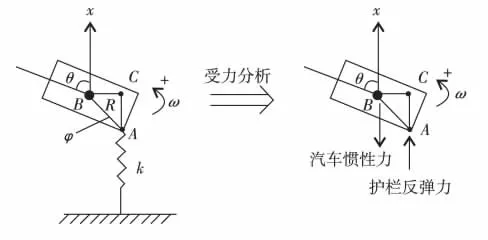
图6 碰撞点为前角点时的汽车受力分析图Fig.6 Mechanical analysis of car when crashing point is front corner point

在考虑汽车转动时，增量等效静力平衡方程为

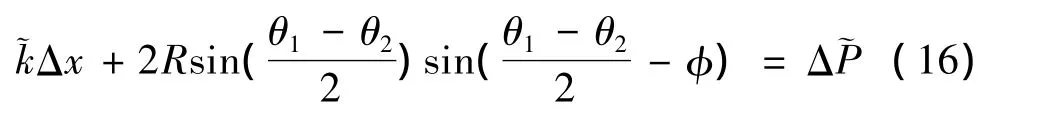
等效刚度和增量等效荷载的表达式为

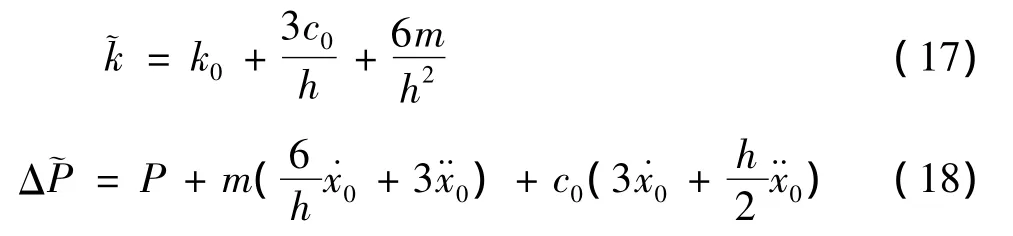
故位移增量和速度增量为

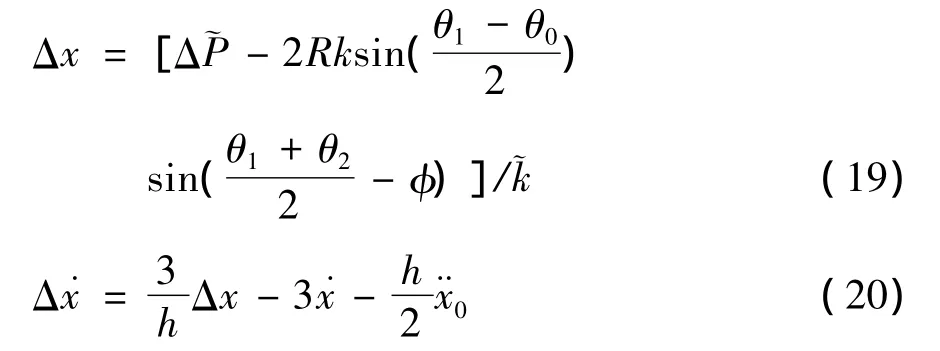
本研究汽车质心B的初始位置xB=xA+R·cos(θ- φ)=1.442，x方向初始速度为 v0=-9.5 m/s，计算时间步长 h=0.01 s.

若能求出汽车轴线与x轴的夹角θ，应用式(16)～(20)，可对汽车碰撞护栏进行时程分析.

在图6中，设汽车质量在平面内均匀分布，则可求得汽车绕质心的转动惯量J为

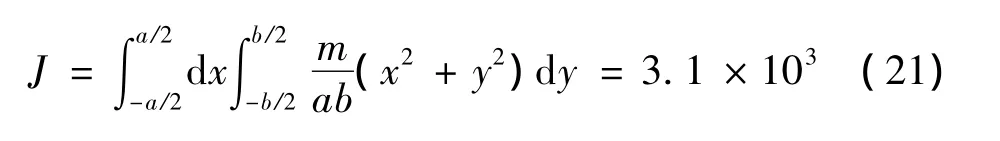
汽车受到绕质心的力矩M为

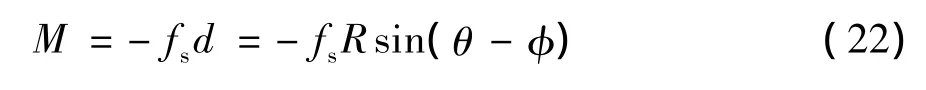
对汽车应用转动定律，则

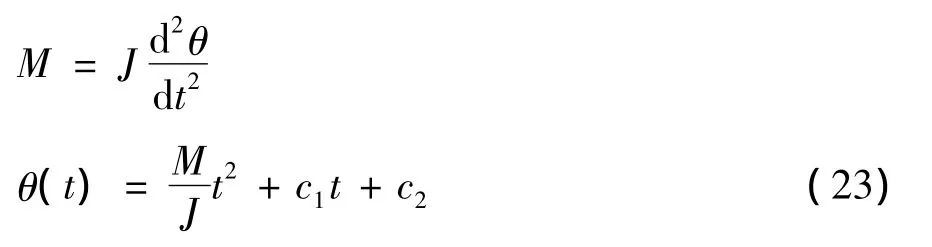
由t0时刻的θ0值，可求得t1时刻的θ1值

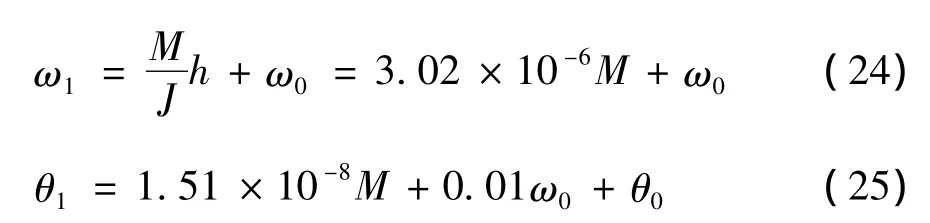
汽车前角点A的x轴坐标值为

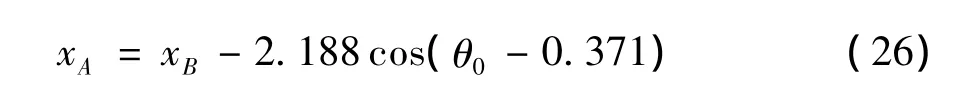
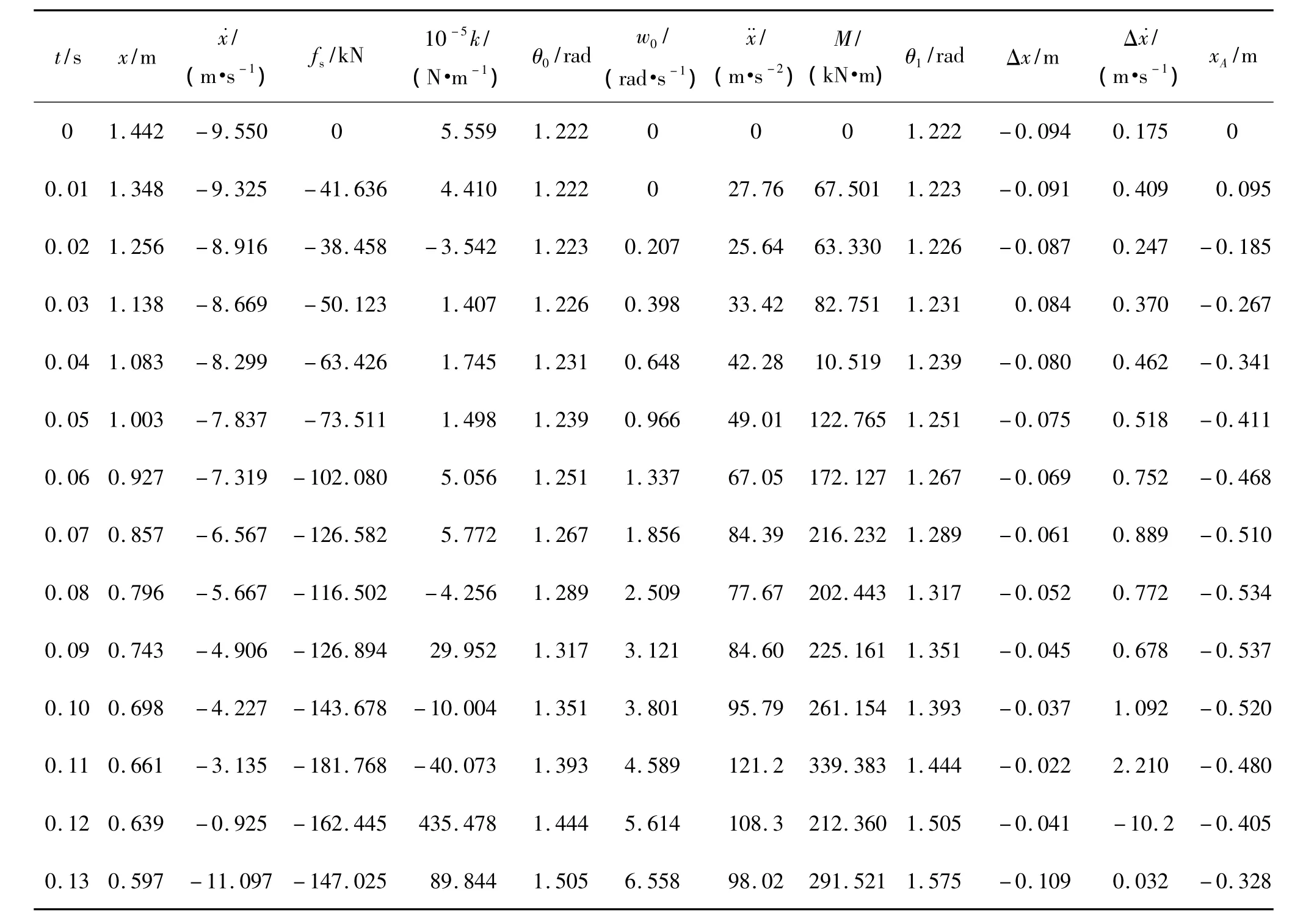
表2 考虑转动汽车碰撞护栏时程分析Table2 Time domain analysis of car crashing barrier process with considering car rotating

3.3 与LS-DYNA模拟结果比较

在汽车与护栏碰撞点在前角点A阶段，xA为护栏的动态变形量.考虑汽车转动的简化计算结果值与有限元结果对比如图7.

图7前部分简化计算和数值模拟吻合，说明考虑汽车转动的Newmark简化计算方法能较准确地对汽车碰撞护栏进行时程分析.与前人的简化计算公式相比，本文考虑了护栏的非线性，精度更高.

3.4 计算补充说明

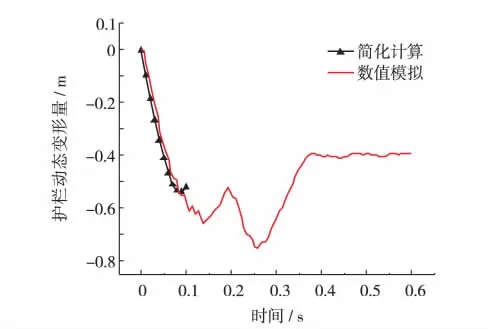
图7 护栏动态变形量结果对比Fig.7 Comparison of barrier dynamic deformation between simplified calculation and numerical simulation

如图8，汽车碰撞护栏可分为3个阶段，即汽车前角点接触护栏阶段、汽车平行护栏阶段和汽车后角点接触护栏阶段.表2仅计算了阶段1，从表2中的θ0可见，在t=0.13 s时，θ0已趋近 π/2，即汽车由阶段2过渡到阶段3.在阶段3时，汽车后角点与护栏接触，其计算模型与阶段1有所不同，如图9，导致图7在0.1 s后简化计算出现突变.

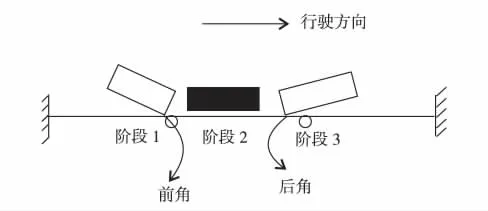
图8 汽车碰撞护栏的3个阶段示意图Fig.8 Schematic of three phases for car crashing barrier process

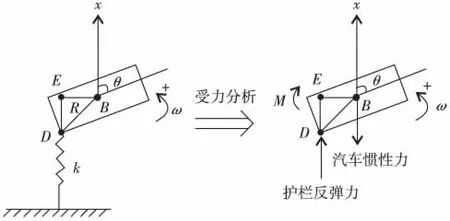
图9 碰撞点为后角点时的汽车受力分析图Fig.9 Mechanical analysis of car when crashing point is back corner point

结 语

本研究提出的简化计算能较准确地对汽车碰撞护栏进行时程分析.采用的理论基础为Newmark β法，分别对不考虑汽车转动和考虑汽车转动建立了简化模型，而考虑汽车转动的简化计算方法能较准确地对汽车碰撞护栏进行时程分析，符合实际，结果更准确.本研究借助了ANSYS求护栏的综合刚度，有待通过简化计算方法以完善.

/References:

［1］LIU Shao-yuan.Dynamic Property Research of Highway Vehicle-barrier Grash［D］.Beijing:Tsinghua University，1994.(in Chinese)刘少源.高速公路汽车与护栏碰撞的动力特性研究［D］.北京:清华大学，1994.

［2］LIU Zhi-bin，ZHOU Yi-ming，FENG Lian-jie，et al.Simulation models of vehicle-barrier crash ［J］.Journal of China Agricultural University，1996(4):56-60.(in Chinese)刘志斌，周一鸣，冯联杰，等.汽车-护栏碰撞的仿真模型 ［J］.中国农业大学学报，1996(4):56-60.

［3］YAO Qi-ming，SUN Li，LI Ming-fei，et al.A study of movement response of vehicle impacting on safety barrier［J］.Journal of Shenyang Architectural and Civil:Engineering Institute，2002，18(4):28-31.(in Chinese)姚启明，孙 利，李明飞，等.汽车冲击防撞护栏的运动响应分析［J］.沈阳建筑工程学院学报:自然科学版，2002，18(4):28-31.

［4］HUANG Xiao-qing，JIANG De-zeng，TANG Li-qun.Nonlinear finite element analysis of semi-rigid guardrail under Impact loading［J］.Journal of South China University of Technology Natural Science，2003，31(3):36-42.(in Chinese)黄小清，江德增，汤立群.冲击荷载下半刚性护栏的非线性有限元分析［J］.华南理工大学学报自然科学版，2003，31(3):36-42.

［5］CHENG Bin，XIAO Ru-cheng.Non-linear programming method for main cable's configuration calculation of selfanchored suspension bridge［J］.Journal of Shenzhen U-niversity Science and Engineering，2008，25(2):140-146.(in Chinese)程 斌，肖汝诚.自锚式悬索桥主缆线形计算非线性规划方法 ［J］.深圳大学学报理工版，2008，25(2):140-146.

［6］Whitworth H A，Bendidi R，Marzougui D，et al.Finite element modeling of the crash performance of roadside barriers ［J］. InternationalJournalofCrashworthiness，2004，9(1):74-79.

［7］Hong H，Deeks J A，Wu C Q.Numerical simulations of the performance of steel guardrails under vehicle impact［J］.Transactions of Tianjin University，2008，14(5):89-93.

［8］Kelafu，PENG Jin.Dynamics of Strectures［M］.WANG Guang-yuan，translate.Beijing:Higher Education Press，2006.(in Chinese)克拉夫，彭 津.结构动力学 ［M］.王光远，译.北京:高等教育出版社，2006.

［9］WANG Hai-bo，CHEN Bo-wang，YU Zhi-wu.A simplified numerical integration format of Newmark-β method for structural dynamic equations［J］.Journal of Sichuan University，2008，40(3):18-20.(in Chinese)王海波，陈伯望，余志武.结构动力方程Newmark-β方法递推简化分析 ［J］.四川大学学报，2008，40(3):18-20.

［10］LI Hong-jing，WANG Tong，LIAO Xu.An interpretation on Newmark betamethods in mechanism of numerical analysis［J］.Journal of Earthquake Engineering and Engineering Vibration，2011，31(2):55-62.(in Chinese)李鸿晶，王 通，廖 旭.关于Newmark-β法机理的一种解释 ［J］.地震工程与工程振动，2011，31(2):55-62.

［11］WANG Hai-bo，CHEN Bo-wang，YU Zhi-wu.A simplified numerical integration format of Newmark-β method for structural dynamic equations［J］.Journal of Sichuan University Engineering Science Edition，2008，40(3):47-52.(in Chinese)王海波，陈伯望，余志武.结构动力方程Newmark-β方法递推简化分析 ［J］.四川大学学报工程科学版，2008，40(3):47-52.

［12］WANG Yuan-feng，CHU De-wen.A coupled precise and finite difference time integration method for structural dynamics［J］.Acta Mechanica Solida Sinica，2003，24(4):69-474.(in Chinese)王元丰，储德文.结构动力方程的精细与差分耦合时程积分法 ［J］.固体力学学报，2003，24(4):69-474.

［13］ZHANG Wu，CHEN Jian，Calculating displacement for automotive engine mounting system based on Newmark［J］.Journal of University of Science and Technology of China，2011，41(12):1090-1094.(in Chinese)张 武，陈 剑.基于Newmark算法的汽车动力总成悬置系统位移计算方法 ［J］.中国科学技术大学学报，2011，41(12):1090-1094.

［14］ZHANG Xiao-qing，HUANG Xiao-qing，TANG Li-qun.Finite element model for dynamic analysis of highway guardrail under impact［J］.Computer Simulation，2007(3):27-30.(in Chinese)张晓晴，黄小清，汤立群.高速公路护栏的冲击动力学分析有限元模型［J］.计算机仿真，2007(3):27-30.

［15］LIU Shao-yuan.A simple simulation method for highway vehicle-barrier crash:flexible beam method ［J］.Journal of Highway and Transportation Research and Development，1995(2):102-110.(in Chinese)刘少源.高速公路汽车与护栏碰撞的简化计算方法—柔性梁法 ［J］.公路交通科技，1995(2):102-110.

［16］DING Hua，JIA Ri-xue，CHU Jin-cao，et al.Study of collisions of vehicles and guard rails［J］.Highway and Transport，1996(3):53-58.(in Chinese)丁 桦，贾日学，储劲草，等.汽车与护拦碰撞特性的研究 ［J］.中国公路学报，1996(3):53-58.

［17］WANG Peng.Research of Composite Impact Barrier for Roads and Highways［D］.Shenzhen:Harbin Institute of Technology of Shenzhen Graduate School，2009.(in Chinese)王 鹏.高速公路复合材料护栏的研究 ［D］.深圳:哈尔滨工业大学深圳研究生院，2009.

［18］LEI Zheng-bao，XIE Yu-hong，LI Hai-xia.The Crashworthiness of Structure with Large Displacement and Large Deformation［M］.Changsha:National University of Defense Technology Press，2005.(in Chinese)雷正保，谢玉洪，李海侠.大变形结构的耐撞性［M］.长沙:国防科技大学出版社，2005.