地震动空间效应对大跨度桥梁非线性地震响应的影响1

黄 信 黄兆纬 胡雪瀛 蔡浩良 齐 麟 刘 涛 王传奇

1）天津市建筑设计院，天津 300074

2）孟菲斯大学，美国田纳西 38152

引言

桥梁地震响应分析方法主要有概率分析方法和确定性分析方法（刘光栋等，1996；林家浩等，2001；范立础等，2001）。概率分析方法是把具有统计性质的地震动作用到结构上求出结构的反应，其建立在地面运动统计特征的基础上，不受任意选择的某一个输入地震波的控制；但由于其数学处理复杂、计算量大，现有研究往往把复杂的实际结构简化成较少自由度的简单结构加以分析。确定性分析方法是以地震动为确定过程的地震反应分析方法，包括反应谱法和动力时程分析法。反应谱法使用简单，但尚难用于多点激励分析，同时对于自振周期超过5s的桥梁结构或当结构在强震作用下进入塑性阶段时则不能直接应用。动力时程分析法主要依据现有地震加速度记录求出结构动力响应，可以分析结构在地震作用下弹性和弹塑性阶段的内力变化，而随着大型有限元软件的发展，现有桥梁地震响应分析主要采用动力时程分析法。动力时程分析法会随输入地震波的不同而有所差异。对于大跨度桥梁结构而言，桥墩之间距离较大，强震发生时行波效应、相干效应以及局部场地效应的影响，会导致地基各点的振动幅值和相位存在较大差异，为合理对大跨度桥梁进行地震响应分析，应考虑地震动输入的空间效应（李忠献等，2003；Dumanogluid等，2003；Lou等，2005；Dameron等，1997；孙建梅，2005；史志利，2003）。行波效应是由于地震波传播速度有限，当支座间距离很大时，必须考虑地震波到达各个支座的时间差。部分相干效应是由于不均匀场地中地震波的反射和折射，以及震源的不同位置传到不同支座的地震波的叠加方式不同，各个支座所受的激励并不完全相干。局部场地效应是因为不同支承处场地条件不同，它们影响地震地面运动的振幅和频率成分的方式不同。同时，对于混凝土桥梁结构而言，地震响应分析中还应考虑材料的非线性（Lee等，1998；黄信等，2010）。

本文考虑地震动输入的空间效应，建立多点激励下大跨度桥梁地震响应分析方法，编制了考虑地震动空间效应的地震动场模拟程序，采用损伤塑性本构模拟混凝土的材料特性，对某大跨度连续刚构桥进行非线性地震响应分析，研究地震动空间效应对大跨度桥梁地震响应的影响，从而为大跨度桥梁抗震设计提供依据。

1 大跨度桥梁动力响应分析方法

1.1 多点激励下桥梁结构动力方程

对于大跨度桥梁结构，多点不同步地震作用下桥梁结构运动方程与一致地震激励下的运动方程不同，此时桥梁结构的动力方程采用分块矩阵形式表示（李忠献等，2003；Dumanog luid，2003；Lou 等，2005；Dameron 等，1997）：

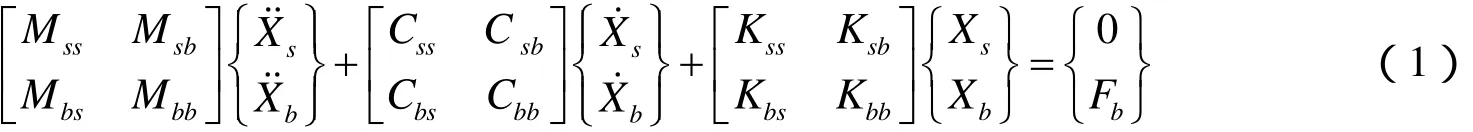
表示地震作用下桥梁结构支座节点的力。

1.2 考虑地震动空间效应的地震动场的模拟

考虑地震场中两测点 k、l，假设它们在地震波传播方向的距离为 d，地震波的主要圆频率为ω，相干函数采用Harichandran模型，自功率谱选取金井清（Kanai-Tajimi）谱（孙建梅，2005；史志利，2003）。

已知自功率谱和相干函数，则n个测点的功率谱密度函数矩阵为：

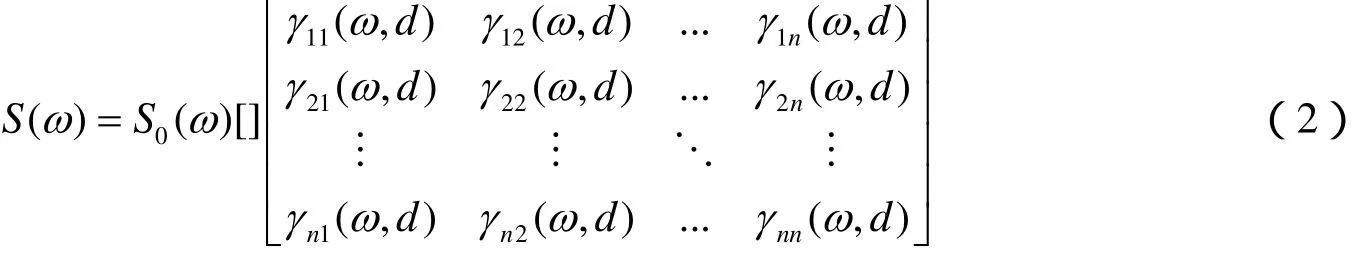
考虑一个零值的一维n变量平稳高斯随机过程 f ( t)，它包含个变量。根据Shinozuka的理论，随机过程的样本可以由下式模拟：

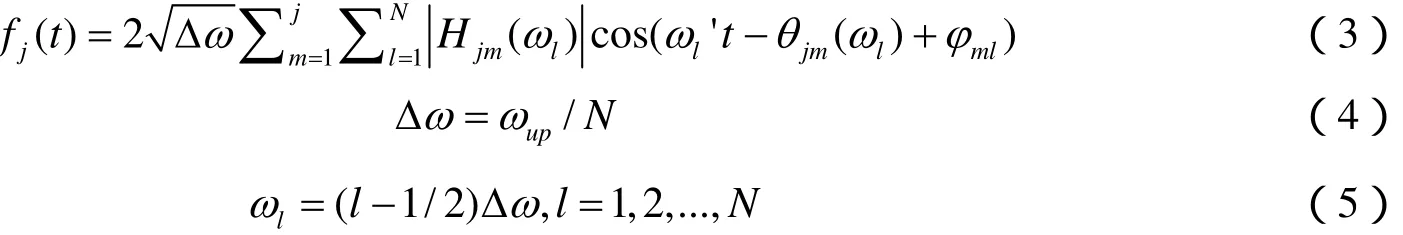
式中，N为一充分大的正整数；ωup为截止频率，当ω＞ωup时，S(ω)=0；δωl为均匀分布于的随机频率；φml为均匀分布与[0，2π)的随机相位角；是各测点间的互谱密度矩阵 S (ωl) 的Cholosky分解矩阵 H (ωl) 中的元素，的幅角。

已知所要模拟的各点的位置关系，可以通过以上引入FFT技术的谐波合成法模拟出符合相应互谱密度矩阵的各点的地震动时程。

1.3 混凝土损伤塑性本构模型

采用损伤塑性模型（Lee等，1998；黄信等，2010），该模型可以用于混凝土材料在动力荷载作用下的受力分析，认为在低静水压力作用下，混凝土材料的损伤主要是由于受拉开裂和受压破碎导致的，该本构模型可以描述混凝土在受拉和受压下的刚度退化、滞回荷载作用下的刚度恢复以及应变率的影响。

通过修正初始弹性刚度考虑材料受力后发生的损伤，建立应力-应变关系如下：

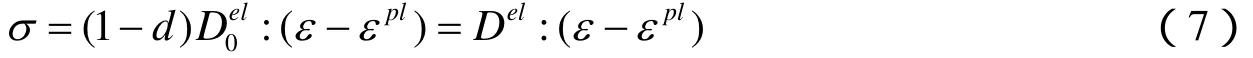
混凝土材料在单轴受拉或受压作用下，由于开裂或压碎产生损伤从而导致刚度下降，此时通过引入损伤因子考虑刚度下降，损伤因子的表达式为：

式中，t、c分别代表拉伸和压缩；β为塑性应变与非弹性应变的比例系数，受压时取0.35—0.7，受拉时取0.5—0.95；inε为混凝土拉压情况下的非弹性阶段应变；kσ为应力；E0为初始弹性模量。

2 地震动空间效应对大跨度桥梁地震响应的影响

为分析地震动空间效应对大跨度桥梁地震响应的影响，本文对某大跨度连续刚构桥进行了地震响应分析。

2.1 分析模型

4跨连续刚构桥上部为变截面预应力混凝土箱梁，桥墩为空心截面桥墩，跨度分别为60m+100m+100m+60m。箱梁为变截面，高为4.4m—8.8m，桥面宽8m，箱梁宽6m；桥墩采用空心截面矩形桥墩，纵桥向宽为8m，横桥向墩顶宽7m，墩顶以下70m按25:1放坡，70m以下按5:1放坡，底部设置5m高的实体墩。上部箱梁结构采用C60混凝土，桥墩结构采用C40混凝土，混凝土材料采用损伤塑性本构（Lee等，1998）。桥梁尺寸如图1所示；桥梁有限元模型如图2所示。

为分析地震动输入对大跨度桥梁地震响应的影响，分别对桥梁采用一致激励、行波激励和考虑相干性的多点激励，加速度幅值取0.2g，地震作用沿纵桥向；利用编制的人工波生成程序生成考虑地震输入空间效应的各个桥墩墩底地震动时程，从而对桥梁进行多点地震激励。一致激励采用生成的第一条地震波作为全桥的地震激励，行波效应采用对第一条地震波进行时间调整而得到不同桥墩墩底处的地震动时程，其中考虑行波效应和多点激励下的视波速分别取100m/s和500m/s。

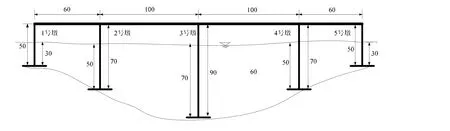
图1 深水连续刚构桥尺寸图（单位：m）Fig. 1 Size and dimension of continuous rigid-framed bridge in deep water (unit: m)

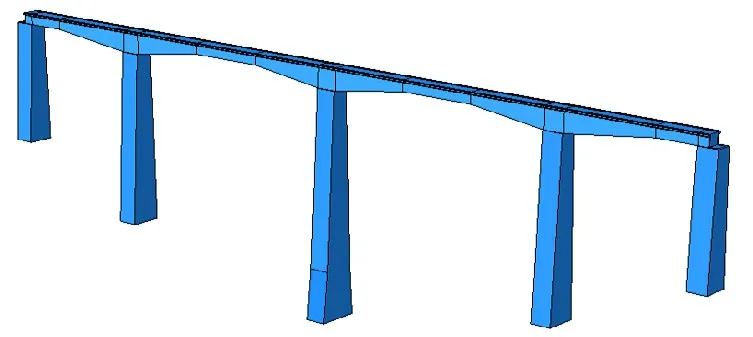
图2 深水连续刚构桥有限元模型Fig. 2 Finite element model of continuous rigid-framed bridge in deep water

2.2 计算结果分析

为分析地震动空间效应对大跨度桥梁地震响应的影响，首先对桥梁上部箱梁结构的动力响应进行分析。表1列出了考虑地震空间效应时地震波作用下桥梁上部箱梁结构的应力响应幅值，其中1号节点至9号节点分别为从1号墩顶到5号墩顶所对应的箱梁及两墩间箱梁的跨中节点，其中应力为Misses应力，为对应截面处混凝土的最大应力。

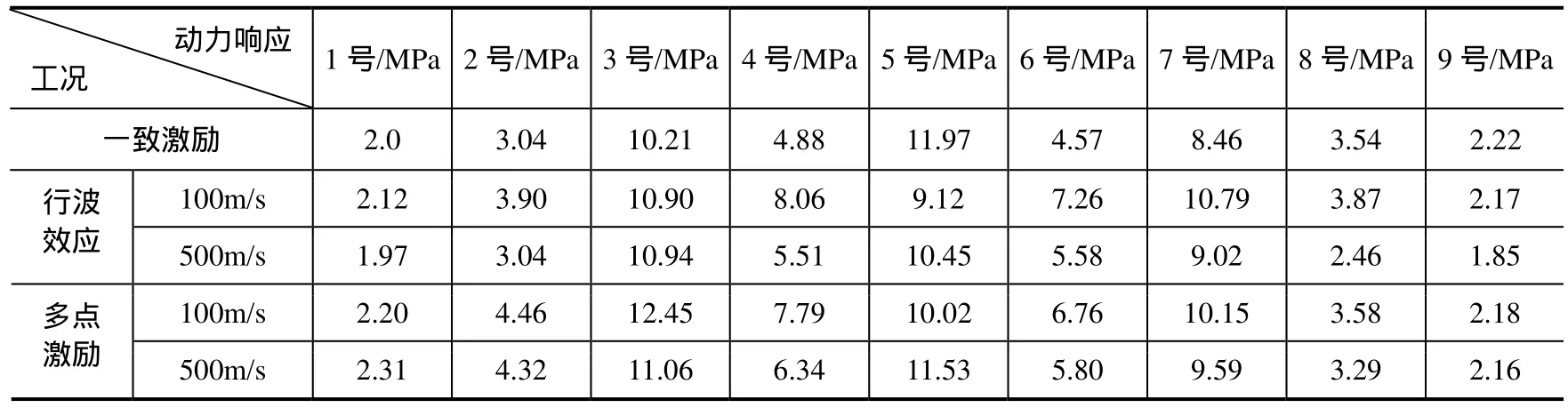
表1 多点激励下桥梁上部箱梁结构应力响应幅值Table 1 Seismic response amplitude of bridge box girder under multi-support excitation

从表1可以看出，在一致激励下1号节点应力为2.0MPa；考虑行波效应，视波速100m/s时1号节点应力为2.12MPa，视波速500m/s时1号节点应力为1.97MPa；考虑多点激励，视波速100m/s时1号节点应力为2.20MPa，视波速500m/s时1号节点应力为2.31MPa。可以看出，考虑行波激励或多点激励时桥梁上部箱梁结构的地震响应较一致激励而言有所差异，考虑地震动空间效应时可能会增大结构响应也可能减小结构响应，往往这种差异不容忽视，如多点激励下视波速500m/s时1号节点应力相对一致激励而言，应力增幅到达15.5%。

由于地震中桥梁发生破坏直至倒塌主要由于桥墩结构发生破坏而引起，所以对桥墩结构的动力响应进行分析。表2列出了地震波作用时桥梁下部桥墩结构的动力响应幅值。

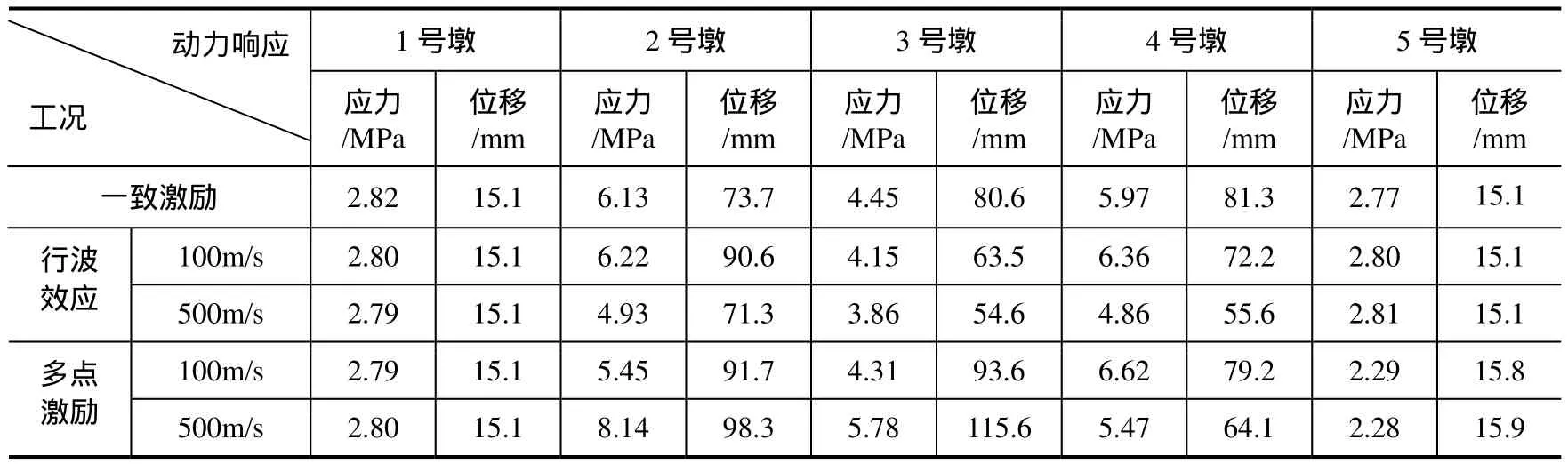
表2 多点激励下桥墩结构动力响应幅值Table 2 Seismic response amplitude of bridge pier under multi-support excitation

从表2可以看出，在一致激励下2号墩墩顶相对位移为73.7mm；考虑行波效应，视波速100m/s时1号墩墩顶相对位移为90.6mm，视波速500m/s时1号墩墩顶相对位移为71.3mm；考虑多点激励，视波速100m/s时1号墩墩顶相对位移为91.7mm，视波速500m/s时1号墩墩顶相对位移为 98.3mm。同样可以看出，考虑行波激励或多点激励时桥墩地震响应较一致激励而言有所差异，考虑地震动空间效应时可能会增大结构响应也可能减小结构响应，往往这种差异不容忽视，如多点激励下视波速500m/s时1号墩墩顶相对位移相对一致激励而言，墩顶相对位移增幅到达33.4%，而行波激励下视波速500m/s时1号墩墩顶相对位移相对一致激励而言，墩顶相对位移减幅为3.3%。

图3和图4分别为一致激励、行波激励和多点激励下，1号桥墩和3号桥墩的墩顶相对位移时程和墩底应力时程。

图3 地震作用下桥墩墩顶相对位移时程Fig. 3 Time-history curve of related displacement on bridge pier top under earthquake action

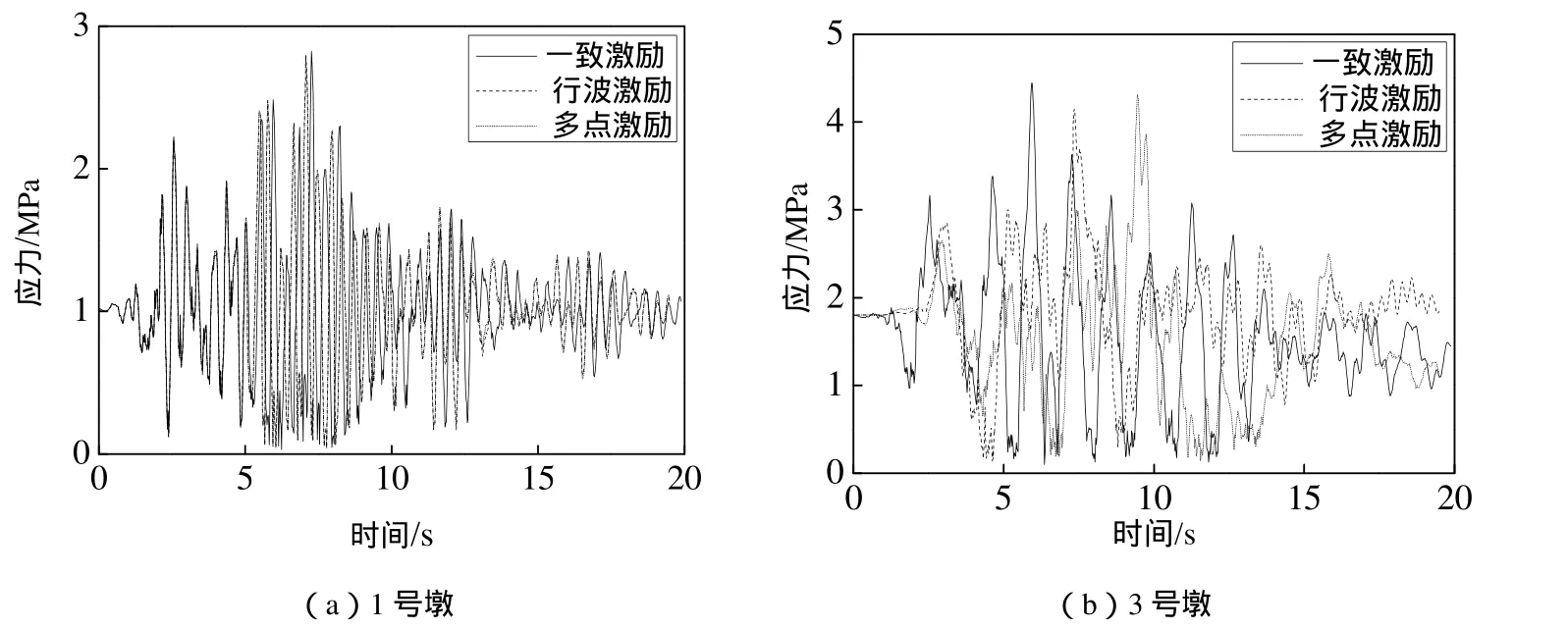
图4 地震作用下桥墩墩底应力时程Fig. 4 Time-history curve of bridge pier bottom stress under earthquake action

通过图3和图4同样可以得到，考虑行波激励或多点激励时桥墩地震响应较一致激励而言有所差异，考虑地震动空间效应时可能会增大或减小桥梁结构的动力响应；所以对于大跨度桥梁地震响应分析应合理的考虑地震动的空间效应，否则会夸大或减小地震作用对桥梁动力响应的影响。同时，从图3（b）可以看出，3号桥墩的墩顶时程随着地震作用的施加而偏离平衡位置，这是由于地震作用下桥墩结构损伤发展而导致混凝土材料出现非线性，说明损伤塑性本构模型能够较好的模拟混凝土材料的非线性行为。

2.3 视波速对桥梁动力响应的影响

为分析多点激励下不同视波速对桥梁地震响应的影响，分别比较行波激励和多点激励下，不同视波速对大跨度桥梁地震响应的影响。

从表 2可以看出，考虑行波激励，视波速 100m/s时，3号桥墩的墩顶相对位移为63.5mm，顶底应力为4.15MPa；视波速500m/s时，3号桥墩的墩顶相对位移为54.6mm，顶底应力为3.86MPa；说明行波激励时，地震对桥梁地震响应的影响随视波速的不同而改变。同样从表2可以看出，考虑多点激励，视波速100m/s时，3号桥墩的墩顶相对位移为 93.6mm，顶底应力为 4.31MPa；视波速 500m/s时，3号桥墩的墩顶相对位移为115.6mm，顶底应力为5.78MPa；说明多点激励时，地震对桥梁地震响应的影响随视波速的不同而改变。

为进一步说明视波速对桥梁地震响应的影响，图 5所示为行波激励下视波速分别为100m/s和500m/s时，1号桥墩和3号桥墩的墩顶相对位移时程；图6所示为多点激励下视波速分别为100m/s和500m/s时，1号桥墩和3号桥墩的墩顶相对位移时程。

通过图5和图6同样可以看出，多点激励时地震对桥梁地震响应的影响随视波速的不同而改变。

综上所述，考虑行波激励或多点激励时桥梁地震响应较一致激励而言有所差异，并且地震动空间效应的影响随着视波速的改变而发生变化；所以对于大跨度桥梁地震响应分析应合理的考虑地震动的空间效应，否则会夸大或减小地震作用对桥梁动力响应的影响。

图5 行波激励下桥墩墩顶相对位移时程Fig. 5 Time-history curve of related displacement on bridge pier top in considering traveling wave

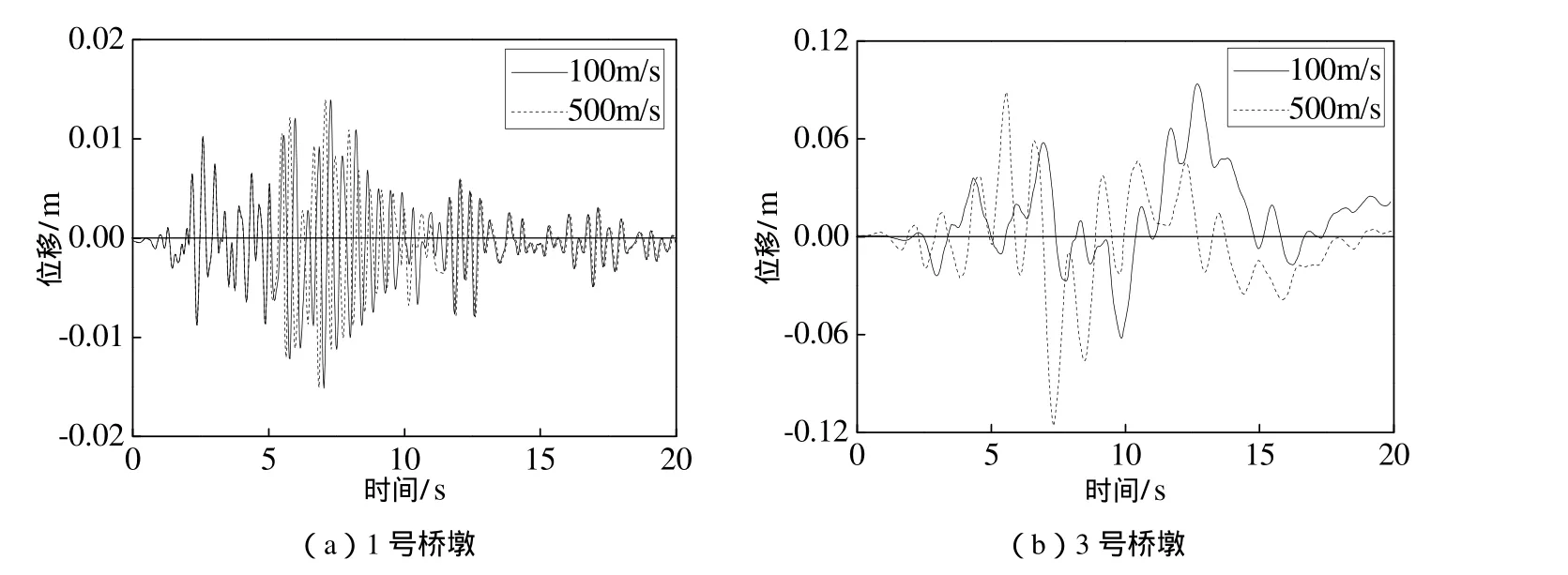
图6 多点激励下桥墩墩顶相对位移时程Fig. 6 Time-history curve of bridge pier bottom stress under multi-support excitation

3 结论

本文考虑地震动空间效应，建立了多点激励下大跨度桥梁动力响应分析方法，并对大跨度连续刚构桥进行了地震响应分析。通过分析得到如下结论：

（1）考虑行波激励或多点激励时桥梁地震响应较一致激励而言有所差异，考虑地震动空间效应时可能会增大结构响应也可能减小结构响应。

（2）考虑多点激励时桥梁地震响应随着视波速的变化而变化，对于大跨度桥梁地震响应分析应合理的考虑地震动的空间效应，否则会夸大或减小地震作用对桥梁动力响应的影响。

范立础，胡世德，叶爱君，2001. 大跨度桥梁抗震设计. 北京：人民交通出版社.

黄信，李忠献，2010. 动水压力作用下深水桥墩非线性地震响应分析. 震灾防御技术，5（3）：352—357.

刘光栋，周建春，1996. 大跨度公路桥梁抗震分析的若干研究进展. 湖南大学学报，23（5）：105—112.

林家浩，张亚辉，赵岩，2001. 大跨度结构抗震分析方法及近期进展. 力学进展，31（3）：350—360.

李忠献，史志利，2003. 行波激励下大跨度连续刚构桥的地震反应分析. 地震工程与工程振动，23（2）：68—76.

孙建梅，2005. 多点输入下大跨空间结构抗震性能和分析方法的研究. 南京：东南大学博士学位论文.

史志利，2003. 大跨度桥梁多点激励地震反应分析与MR阻尼器控制. 天津：天津大学博士学位论文.

Dumanogluid A.A., Soyluk K., 2003. A stochastic analysis of long span structures subjected to spatially varying ground motions including the site-response effect. Engineering Structures, 25 (10): 1301—1310.

Dameron R.A., Sobash V.P., Lam I.P., 1997. Nonlinear seismic analysis of bridge structures foundation-soil representation and ground motion input. Computers & Structures, 64 (5-6): 1251—1269.

Lee J., Fenves G.L., 1998. A plastic-damage concrete model for earthquake analysis of dams. Earthquake Engineering and Structural Dynamics, 27 (9): 937—956.

Lou L., Zerva A., 2005. Effects of spatially variable ground motions on the seismic response of a skewed,multi-span, RC highway bridge. Soil Dynamics and Earthquake Engineering, 25 (7-10): 729—740.