活动标架在对象识别中的应用＊

姚若侠，袁 伟，成丽美

(陕西师范大学 计算机科学学院，陕西 西安 710062)

0 引言

19 世纪早期，法国数学家Cartan［1-2］融合了Darboux，Frenet，Serret 和Cotton 的早期工作，提出并发展了活动标架理论的现代方法，其核心工作是将活动标架转变为一种强大的计算工具，并借助该方法分析子流形的几何性质和变换群作用下的微分不变量.20 世纪70 年代，研究人员［3-5］开始试图将Cartan的直观构造方法归纳为坚实的理论基础.近年来，Fels 等［6-7］摆脱了狭隘的框架束缚，建立了一个新的、强大的、具有建设性的方法，该新方法定义活动标架为一个从子流形或者Jet 丛(射流丛)到群变换的等变映射.这一定义的给出引发了一个极其重要的概念上的跳跃，从而将活动标架理论从对任何形式标架丛或联络的依赖中分离出来.该方法可被系统地应用于一般变换群，且所有经典的活动标架都可以用这种方法重新诠释.

Cartan 的活动标架规范化构造方法的关键点就是要相对于群轨道选择若干横截面，这样就可以通过规范化系统的选定构造等变活动标架，并通过诱导的不变化过程产生不变量的完备系.理论上，活动标架存在的必要条件是群作用必须是自由的.经典地，对于非自由的群作用，可以将它延拓到Jet 空间构造基本微分不变量和高阶微分不变量［8］.

现代图像处理的首要目标就是在不同方向、不同位置，甚至有某些形变的情形下去识别这些对象.在识别过程中，目标对象首先需要用其边界轮廓曲线去表示.若已知一个变换群作用，我们的任务就是要确定2 个对象是否能够通过一个变换相互映射，也就是说，2 个对象的边界曲线在群作用下能否匹配.实际上，这一匹配问题，或者说轮廓曲线的重叠问题就约化为边界曲线的对称分类问题.受到Cartan关于等价问题解［9］和活动标架的等变映射方法的启发，Calabi［10］提出了微分不变签名曲线，它由曲率和曲率关于弧长的导数这2 个不变量参数刻画.在欧几里得群变换下，任意曲线都能被签名曲线唯一描述，也就是说，平面上的任意一条曲线，它的签名曲线不会因为曲线的平移和旋转而发生改变.因此，签名曲线能很自然地应用于计算机对象识别领域.与传统的方法相比，签名曲线的曲率和曲率关于弧长导数的刻画方式在对象识别中扮演着重要角色，它避免了曲线初始点选择的影响，消除了曲线重新参数化的计算困难，并且很容易被扩展到空间曲面和更高维的子流形上［11］.

1 等变活动标架和微分不变量

1.1 等变活动标架

一般来说，群G 作用于空间M 和N 上，若存在一个映射φ:M→N，满足φ(g·z)→g·φ(z)，对∀g∈G，z∈M 都成立，则φ 是左等变映射.类似地，若满足φ(g·z)→φ(z)·g-1，则称φ 为右等映射.

定义1 给定作用在流形M 上的变换群G，则活动标架是一个光滑的G 等变映射

定义2 给定一个光滑的映射ρ:M→G，对∀g∈G，z∈M，若ρ(g·z)→g·ρ(z)，则ρ=ρ(z)是一个左G 等变映射;若ρ(g·z)→ρ(z)·g-1，则ρ 是一个右G 等变映射.一个左(右)活动标架是一个左(右)G 等变映射.

定理1 活动标架在点x∈M 的一个邻域内存在，当且仅当G 在点x 附近的作用是自由和正则的.对∀x∈M，g∈G，函数F:M→G 是一个G 不变的函数，则

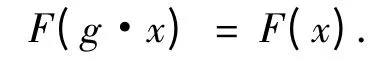
定义3 对∀x∈M，g∈G，若I(g·x)=I(x)，则实值函数I:M→R 是群G 的不变量.若存在单位元e∈G 的一个邻域N，对∀x∈U，g∈N，使得I(g·x)=I(x)，则实值函数I:U⊂M→R 是局部不变量.

1.2 活动标架的构造

若已知一个正则的群作用，则基于Cartan 的规范化方法［12-13］，便可获得该群的一个基本不变量完备集，该方法几乎完全依赖于横截面的选取.

定义4 群G 正则作用于m 维流形M，其轨道为s 维，一个截面是流形M 的m -s 维子流形K，且K 与每个轨道都恰好横截于一个点.

定理2 设群G 自由且正则地作用于流形M 上，K 为一个截面.给定z∈M，设g=ρ(z)是唯一一个将z 映射到截面K 上的群元素:g·z=ρ(z)·z∈K，则ρ:M→G 是该作用的一个右活动标架.

给定M 上的局部坐标x=(x1，x2，…，xm)，变换群G 的群参数g=(g1，g2，…，gr)，下面介绍规范化方法，这是活动标架方法的核心内容.

假设G 正则地作用于M，为简单起见，就G 本身而言，假定它的轨道维数相同且都为r.也就是说，假定G 作用是局部自由的，那么构造活动标架和不变量的主要步骤为:

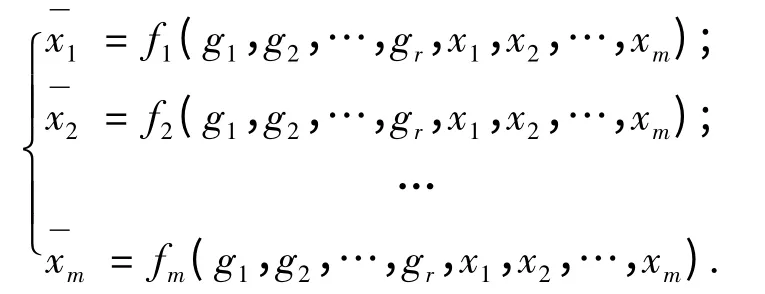
第2 步:在实数集R 上恰当地选择r 个常数，即c1，c2，…，cr∈R，令坐标变换等于这些常数，即得规范化方程组

第3 步:对于群参数集g=(g1，g2，…，gr)，求解规范化方程组，即得到群参数用局部坐标表示的形式.若方程组的解

是一个光滑映射，则式(2)是一个右活动标架.

第4 步:计算其他坐标在已获得的活动标架下的作用，可得局部不变量的基本完备集

特别地，在第3 步中，常数可以任意选择，但有些情况不能选为0，这需视具体情况而定.除此之外，参数的选择必须要使这个正规化方程组的解存在，这些常数定义了一个截面.为了简化计算过程，参数的选择应尽可能地使这些常数为0 或者1.值得注意的是，假定群变换参数为r 个，则选择一个横截面K，使得K={x1=c1，x2=c2，…，xr=cr}.所以，活动标架即是将点x 映射到由横截面K 和经过点x 的轨道的交点的变换.

定理3 给定一个自由且正则的群作用和一个坐标截面，设g=ρ(z)为正规化方程组的解.若g 是一个光滑映射，则活动标架和方程

组成了一个与群作用的函数无关的局部不变量完备系.

1.3 微分不变量及其构造

定义5 令G 是一个点变换或者切变换群.微分不变量是一个实值函数I:Jn→R，对于所有的z(n)=(x，u(n))，满足I(g(n)·(x，u(n)))=I(x，u(n)).其中:Jn=Jn(M，p)是n 阶扩展的Jet 丛;p ＜m(m 是流形M 的维数).特别地，J0=M，g(n)·(x，u(n))是延拓变换群.

一个n 阶的活动标架ρ(n):Jn→G 是定义在Jet 空间的开子集上的等变映射，只要n 足够大，延拓群G(n)在稠密开子集vn⊂Jn上是正则且自由的.

定理4 n 阶活动标架在点z(n)∈Jn的一个邻域内存在当且仅当z(n)∈v(n)是正则的.

考虑作用于平面曲线u=u(x)上的特殊欧几里得群SE(2):

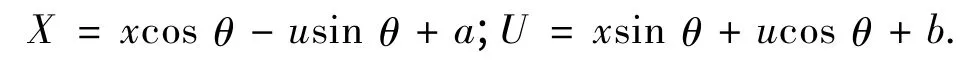
该群作用的一阶延拓定义了一个作用于J1(R2，1)的自由群

这里，通过选择一个好的横截面{x=0，u=0，ux=0}可获得J1(R2，1)上的一个活动标架.求解对应的规范化方程组X=U=UX=0，得到右活动标架

延拓群作用到Jm并取规范化常参数，可以获得m 阶的基本微分不变量集.简单地，取m=3，计算可得:

将式(3)分别代入式(4)和式(5)，可得基本微分不变量

2 数值不变签名曲线

定义6 在平面上，若定义了G 的不变曲率κ 和它的关于弧长的导数，且它们是解析的，则曲线C是G 规则的.

定义7 非退化的规则平面曲线的G 不变签名曲线S 由κ 和κs参数化，即

定理5 一般的r 维变换群G 作用于R，在群G 作用下，当且仅当2 个G 规则的非退化解析曲线C和C 的签名曲线是相同的，即S=S 时，它们是等价的.

在实际应用中，可以通过离散的数值逼近来计算微分不变量.一个鲁棒且高效的数值方法是解决问题的关键所在，但是许多重要的微分不变量阶数比较高，对舍入误差和噪音很敏感.为了解决这个难题，本文使用联合不变量为κ，κs找到数值表达式，以期获得不敏感的逼近.

特别地，在子流形中，任何离散的逼近方案最终都将依赖于网点或者离散点的引入，然后，构造网点坐标的特定结合，这些网点将会逼近微分不变量的值.由于变换群下的逼近是不变的，因此，微分不变量的数值不会受到群作用的影响.一般地，若G 是一个作用于空间E 上的群，则联合不变量［14］是依赖于有限个点x1，x2，…，xn的函数J(x1，x2，…，xn).从点的配置上看，这些点在群元素g∈G 的同步作用下是保持不变的.例如，对于欧几里得群，联合不变量是点P，Q 之间的欧几里得距离d(P，Q)的函数.类似地，对于等仿射群，给定三角形的3 个顶点P，Q，R，最简单的结合不变量就是三角形的面积A(P，Q，R)，也就是说，每个联合不变量是这些三角形面积的函数.Green［4］的研究结果给出了曲线的微分不变量个数和群作用的联合不变量的个数之间的关联，用于形成更实际的联系，建立了离散的和连续的不变理论的桥梁［15］.因此，使用一个有限差分逼近方法为一个微分不变量I 构造数值逼近，以便用网点坐标的结合来计算这个逼近.于是，任何对于微分不变量的G 不变数值逼近一定会由G 的联合不变量的一个函数控制.我们将通过平面上的欧几里得曲线详细介绍数值不变签名曲线的求解过程.

对于包含了旋转和平移变换的特殊欧几里得群SE(2)，依据Weyl［16］的方法，欧几里得群的每个联合不变量都是欧几里得距离d(P，Q)=|P-Q|的函数和位移向量之间的交乘(P -Q)∧(R -S).对于一个规则，光滑的平面曲线C，其欧几里得群最简单的微分不变量是欧几里得曲率κ.曲线在点P∈C 处的曲率的绝对值是其内切圆半径的倒数.通常，若曲线的方程为u=u(x)，且u(x)具有二阶导数，则曲线u=u(x)在点(x，u(x))处的曲率为

对于凸曲线，曲率是正的;反之，凹曲线的曲率是负的.

从定理6 可以看出，尽管曲线关于弧长的连续导数导致无限多个更高阶微分不变量，但是只需要考虑前2 个微分不变量κ 和κs就能够完全刻画曲线.

接下来，用联合不变量逼近微分不变量来说明本节讨论的理论体系，描述如何用标准的几何构造来获得一个数值逼近.当然，对于欧几里得曲率，因其在刚体运动下不受影响，故曲线的任何平移或旋转运动都有相同的数值逼近.鉴于欧几里得联合不变量的特征，迫使这个逼近只能依靠网点间的距离来实现.此外，因为曲率是二阶微分函数，所以要求取3 个网点来逼近.

图1 曲率逼近

由于式(6)仅依赖于点之间的距离，所以，对于曲线L 上的中间点B，它给出了该点曲率的完整的欧几里得不变数值逼近.

同样的方法也可用于逼近高阶微分不变量κs，则κs在点Pi处的有限差商表达式为

由于选择的点不是对称的，因而导致了数值偏差，所以要选取的点必须是对称的，从而κs的中心差商表达式为

这样，要想获得签名曲线的欧几里得不变离散逼近，必须使用(κ(Pi-1，Pi，Pi+1)，κs(Pi-2，Pi-1，Pi，Pi+1，Pi+2))作为要逼近的点.

3 例证结果与分析

为了简单地说明曲线的数值不变签名曲线的求解问题，笔者选取了2 个具有函数表达式的曲线，当然，这个方法可以用于任何曲线.通过离散化极坐标上的角度来实现曲线上点的选取，进而使用数值方法实现不变签名曲线的构造.

图4 左侧为极坐标方程r2=3 +cos(3θ)的原始曲线图，右侧为r2的旋转一个角度后的曲线图;图5为图4 中的2 条曲线的签名曲线，左图为连续曲线，右图为离散曲线.由于旋转比平移稍复杂一些，本文以旋转为例来说明刚体变化.可以看出:尽管曲线发生了刚体变化(如平移、旋转)，但它的签名曲线是一样的.由此可见，任何发生刚体变化的对象都可以通过它们的签名曲线来分类和识别.也就是说，只要对象的签名曲线是相同的，那么它们就是同一个对象.

图2 r1=的连续原始曲线和离散原始曲线

图3 有偏差和无偏差的离散签名曲线

图4 r2=3 +cos(3θ) 的原始曲线和旋转一个角度后的曲线

图5 连续和离散的签名曲线

4 结语

在计算机对象识别中，可以将对象的轮廓提取出来，方法之一就是将对象识别的问题转化为曲线的识别问题.在实际应用中，被识别的对象可能会由于某种原因发生了旋转和平移变化，甚至某种程度上的扭曲(仿射变化)，导致对象难以识别.使用签名曲线可以很好地解决这个问题，因为任意曲线的签名曲线唯一地刻画了这个曲线，且不会随着对象的旋转和平移发生变化.对于仿射变化，可以用同样的数值方法进行仿射逼近来获得其签名曲线.与刚体变化所得的结论一样，对象的签名曲线不会随着对象的仿射变化而发生变化，所以可以通过比较签名曲线而不是比较曲线本身来获知曲线是否匹配，这在很大程度上降低了识别的复杂度.

［1］Cartan É.La méthode du Repére mobile，la théorie des groupes continus，et les espaces généralisés，exposés de géométrie［M］.Paris:Hermann，1935.

［2］Cartan É.La théorie des groupes finis et continus et la géométrie différentielle traitées par la méthode du repére mobile［M］.Paris:Gauthier-Villars，1937.

［3］Griffiths P.On Cartan′s method of Lie groups as moving frames as applied to uniqueness and existence questions in differential geometry［J］.Duke Math J，1974，41(4):775-814.

［4］Green M L.The moving frame，differential invariants and rigidity theorems for curves in homogeneous spaces［J］.Duke Math J，1978，45(2):735-779.

［5］Jensen G R.Higher order contact of submanifolds of homogeneous spaces［M］.New York:Springer-Verlag，1977.

［6］Fels M，Olver P J.Moving coframes I:A practical algorithm［J］.Acta Appl Math，1998，51(2):161-213.

［7］Fels M，Olver P J.Moving coframes II:Regularization and theoretical foundations［J］.Acta Appl Math，1999，55(2):127-208.

［8］Olver P J.Generating differential invariant［J］.Math Anal Appl，2007，333(1):450-471.

［9］Olver P J.Equivalence，invariants，and symmetry［M］.London:Cambridge University Press，1995.

［10］Calabi E，Olver P J，Tannenbaum A.Affine geometry，curve flows，and invariant numerical approximations［J］.Adv In Math，1996，124(1):154-196.

［11］Hoff D J，Olver P J.Extensions of invariant signatures for object recognition［J/OL］.J Math Imaging Vis，2012，DOI:10.1007/s10851-012-0358-7.

［12］Killing W.Erweiterung der begriffes der invarianten von transformationgruppen［J］.Math Ann，1890，35:423-432.

［13］Weiss I.Geometric invariants and object recognition［J］.Int J Comp Vision，1993，10(3):207-231.

［14］Olver P J.Joint invariant signatures［J］.Found Comp Math，2001，1(1):3-68.

［15］Sturmfels B.Algorithms in invariant theory［M］.New York:Springer-Verlag，1993.

［16］Weyl H.Classical Groups［M］.Princeton:Princeton Univ Press，1946.