磨床工作台T形槽与螺栓接触问题有限元分析*
刘晓明,李少波
(贵州大学教育部现代制造技术重点实验室,贵阳 550003)
0 引言
T形槽是一种广泛应用于工作台上的夹具,它通常与T形螺栓相配合,来达到固定部件的目的。本文所研究的T形槽位于高精度数控工具磨床工作台,T形槽本身的加工精度要求较高的同时,其与T形螺栓配合过程中,也要求具有较好的力学性能以及密封特性,保证夹紧装置的稳定性与可靠性,确保工作台磨削和进给工作的正常进行,从而保障数控磨床的磨削精度[1]。ADINA是一款大型商用专业有限元求解软件,专注求解结构动力学、流体动力学、结构与流体耦合、热-机械耦合等复杂的线性与非线性多场耦合分析[2]。借助于ADINA系统,用户能够有效的处理复杂结构的计算分析,在大、小型的变形、应变;静力学和动力学中的接触问题、子结构分析;线性化的屈曲分析等工程应用方面均可以获得较为理想的精度[3,4]。本文借助ADINA平台对高精度数控磨床回转工作台中的夹紧装置T形槽与T形螺栓连接的接触问题、结构可靠性进行了有限元分析优化。
1 理论基础
接触问题广泛存在于各种工程结构中,在接触面附近区域存在较大的应力集中,是复杂的非线性问题。随着接触载荷的增加,接触面几何状态可能发生变化,两物体相互接触时,接触面附近很小的区域内有较大的应力峰值。在弹性范围内,T形槽与T形螺栓接触问题的分析基础是赫兹理论。赫兹理论的一般解法需要三个前提条件:①相互接触物体的材料应是匀质和各向同性的;②接触处形成的压力面应是平坦面,并且压力面的长短轴线与接触处曲率半径的比值应很小;③不能超过材料的弹性极限[5]。
2 接触建模与有限元分析
选择合理的T形槽几何参数对保证数控磨床及其高精度回转工作台长期稳定运行非常重要。然而,操作条件不同则对应的T形槽几何参数优化值也不同[6],本文根据 T形槽标准尺寸(GB/T158-1996),参考回转工作台具体的操作条件、工作转速及压力,选择适合回转工作台尺寸的T型槽尺寸如图1所示。
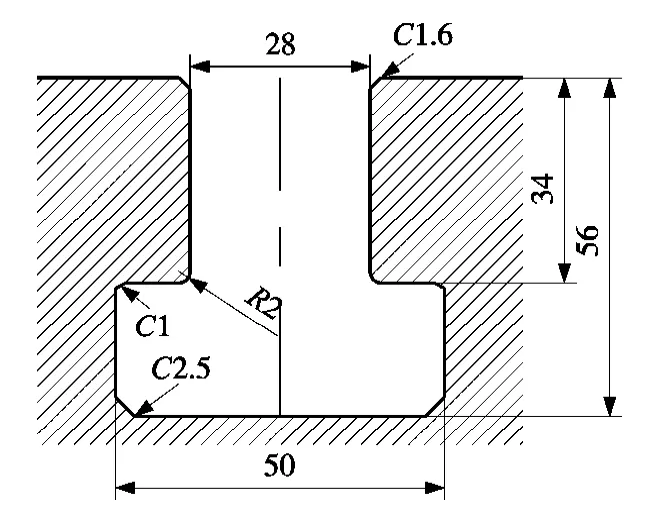
图1 T形槽选用尺寸
T形槽与T形螺栓接触问题是多体接触、摩擦、滑动、材料非线性问题、几何非线性问题的复合接触问题,为了便于T形槽与螺栓接触的分析,有必要对其进行合理的简化:现将该接触模型转化为块体与刚性柱体的挤压接触问题,忽略该接触问题中涉及到的几何非线性和材料非线性问题,使轴承接触问题归属于纯边界非线性问题。在此模型中,暂不考虑接触过程中的各向旋转以及水平方向的移动,只考虑T形槽与螺栓接触法向的正压力分析。二维简化模型如图2所示。

T形槽与螺栓接触二维简化模型
使用ADINA有限元分析软件通过创建点、线、面建立T形槽与T形螺栓的二维有限元模型,并设置杨氏模量为1×106MPa,泊松比为0.3。基本模型建立后,需要对块体和刚性柱体进行网格划分以及接触控制,并定义载荷,如图3所示。

图3 施加载荷的模型网格图
此时模型中弧线上的点仅仅位于接触面上,而与任何单元都不相连,这些节点被自动固定。然后应用到ADINA软件的后处理程序中,使两个体进行接触并查看应力矢量。如图4所示。

图4 应力矢量图
启动ADINA有限元分析求解,在首次运行校验模型后,查询多个时间步,查看运行结果。如图5所示。

图5 各阶段时间步
T形槽物理特性、载荷和边界条件直接分配到模型的几何图形上,修改有限元网格,不受模型清晰度的影响,灵活控制单元大小分布,有效的进行线性分析。这时再运行后处理文件,就可以看到T形槽与T形螺栓接触模拟变形图,变形结束后的模型如图6所示。
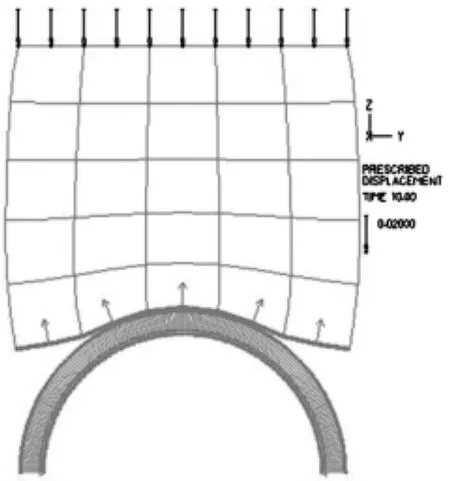
图6 模型变形图
根据变形情况,我们已经了解T形槽与T形螺栓接触的中心处变形量最大,但是其具体的变形位移以及块体内部实际应力情况,图6的模型图中并没有显示出来。因此应用ADINA有限元分析软件对上述模型进行应力分析。得到如图7所示的各阶段应力和载荷云图,可以分析出在初期时间步TIME2.000时,有效应力最大为81859Pa,最小有效应力为319.9Pa;中期时间步TIME6.000时,最大有效应力为209065Pa,最小有效应力为413.9Pa;末期时间步TIME10.00时,最大有效应力为310292Pa,最小有效应力为679.2Pa。

图7 各阶段应力和载荷云图
两者最终状态时接触应力分布以及位移变化情况,如图8所示,可明确观察到应力集中点与位移变化程度。

图8 接触应力云图
3 有限元分析的理论验证
根据赫兹理论,圆柱与平面之间的接触应力曲线应该是连续光滑的,在接触点处的几何学关系上有如下两个函数[7]:
主曲率和

主曲率差

对于弹性模量E=1X106MPa及泊松比μ=0.3的钢,根据赫兹理论可推出下式:

式中:a——压力面椭圆的长轴,mm;
b——压力面椭圆的短轴,mm;
Q——法向载荷,MPa;
Pmax——最大接触应力,MPa;
δ——为弹性趋近量,mm。
a*、b*可查表求得。由赫兹理论推导出的公式(5)、(6)可知,在压力一定的情况下,最大接触应力和弹性趋近量受a*、b*以及主曲率和的影响,而a*、b*是根据主曲率差查表得出,因此,最大接触应力和弹性趋近量最终取决于主曲率和与主曲率差。
计算求得理论最大接触应力Pmax=309239Pa,弹性趋近量δ=0.0528mm;在有限元软件分析的结果中,最大接触应力为310292Pa,弹性趋近量为0.0552mm。对比理论计算值与数值模拟值,最大接触应力的相对误差:
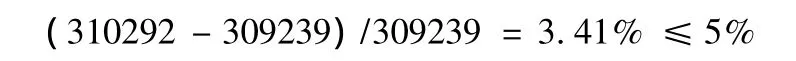
弹性趋近量的相对误差:

符合工程设计要求。
4 结束语
应用ADINA对磨床回转工作台T形槽与T形螺栓连接接触问题进行分析,可以得出以下结论:
(1)T形槽在正压力与T形螺栓挤压力的作用下,各网格单元的变形并不均匀;
(2)在两者接触面的法向方向上,T形槽由两边至中间也即压力作用中心,有效应力逐渐增大,形变位移渐变明显。
(3)得出的有限元解与赫兹理论解的误差较小,最大接触应力的相对误差为3.41%,弹性趋近量的相对误差为4.35%,数值模拟与理论计算相印证,均满足工程设计要求。
根据有限元分析,可以较为直观的获得T形槽应力与应变的分布情况,预测危险截面所在区域,从而为结构优化、工艺选取提供可靠地依据,保证磨床及其回转工作台的精度与稳定性。
[1]高红娟.高精度数控联动回转工作台关键技术的研究[D]. 苏州:苏州大学,2010.
[2]杨立权,杨立专,吕青青,等.平板孔口应力集中的数值模拟及理论分析[J].煤矿机械2012,33(2):65-67.
[3]朱诗顺,鲁广文.TZI720支架立柱强度及变形模态的有限元分析[J]. 煤矿机械,1995,16(06):4-6.
[4]王自勤,陈家兑,何玲,等.复杂零件的精确建模及有限元分析[J].机械与电子,2006(4):27-29.
[5]张晓东,唐南.同质体接触问题有限元分析[J].设计与研究,2012,39(1):39-41.
[6]郭增杰,李一平.电镀CBN组合砂轮磨削组合夹具T形槽初步探讨[J].磨料磨具与磨削,1991,8(63):16-20.
[7][英]K.L.Johnson著,徐秉业,等,译.接触力学[M].北京:高等教育出版社,1992.

