组合数学课程的教学实践

刘瑞芳，贾会才

(1.郑州大学 数学系，河南 郑州 450001； 2.河南工程学院 数理科学系，河南 郑州 451191)

组合数学又称离散数学，通常也把组合数学和图论加在一起称为离散数学.组合数学是计算机出现以后迅速发展起来的一门数学分支.计算机科学是算法的科学，而计算机所处理的对象是离散的数据，所以离散对象的处理就成了计算机科学的核心，研究离散对象的科学就是组合数学.组合数学的发展改变了传统数学中分析和代数占统治地位的局面.

组合数学作为一门重要的数学课程，在教学中如何引入与展开才能使学生更好地学习和掌握就成了一个重要的课题.组合数学有别于其他一些数学课程的是它与实际问题联系密切，强调数学应用能力和创造能力的培养.组合数学解决问题的方法没有连续性和固定套路，往往一个问题一种解法，这些特征促使教师在教学中要避免填鸭式的讲授，要在讲解知识的过程中激发学生的学习兴趣和创造性思维能力.下面将结合教学中的实践来论述组合数学教学的引入与展开方法.文中所涉及的一些概念和术语如无详细说明，可参见文献[1-3].

1 课程设计

学生经过几年数学基础课和专业课的学习之后,很容易对数学产生枯燥、难懂、脱离实际的印象，组合数学课正好为改变学生的这些想法提供了一个契机，要通过第一堂课的引入使学生对课程产生兴趣.

例1 甲、乙两个人轮流从k堆钱币中取钱，每次选定一堆，从中至少取出一个钱币(可全取)，取到最后一个钱币者胜(组合数学中著名的Nim对策).

例2 猎人带着一担白菜、一只羊和一条狼要过河，但是只有一条小船，只有猎人会划船并且他一次至多只能带白菜、羊和狼三者之一过河.如果让狼和羊在一起而猎人不在旁边的话，狼就会把羊吃掉；如果让羊和白菜在一起而猎人不在旁边的话,羊就会把白菜吃掉.问如何让他们都平安过河?(组合数学中著名的船过河问题)

组合数学中类似的有趣问题非常多，如河洛图(幻方)、稳定婚姻问题、铺地砖问题等.这样的课程引入方式通过一个个生动有趣的问题组成了别致而生动的第一堂组合数学课，完全显示了组合数学的神奇和奥妙.

2 教学中的引入与展开

2.1 激发学生的学习兴趣

课程有了一个好的引入方式，能给学生带来轻松的气氛，进一步展开课程以激发学生的学习兴趣就成了下一个问题.在实际的教学中，可以从贴近生活的一个个有趣的例子入手来讲解组合数学中重要的原理和概念，比如组合数学中重要的鸽笼原理.要想很好地运用鸽笼原理激发学生的学习兴趣,可以从日常生活中有趣的小问题入手.

例3 某棋手有11周的备战训练，每天至少下一盘棋，但每周不超过12盘.试证：必有连续的若干天恰好下21盘棋.

例4 100个人参加一个聚会，其中每个人都有偶数(可能是零)个朋友.证明：在这100个人中必定有3个人有相同数目的朋友.

给半小时的时间让学生自己试着证明上述两个贴近生活的例子，学生们在独立思考与激烈争论之后无形中已经分别用了鸽笼原理的简单形式(n+1个球放入n个盒子中，必有一个盒子含有两个或者更多的球)和平均形式(将nr+1个球放入n个盒子中，必有一个盒子至少含有r+1个球)解决了例3和例4.最后，教师可再提出鸽笼原理，并指出鸽笼原理运用的关键是如何合理地选择鸽子和笼子.这样的讲授方式学生很容易理解，可以激发学生学习鸽笼原理的积极性，让学生感觉到学习组合数学简单有趣，学习兴趣得到了极大提高.

2.2 调动学生的学习主动性

教师可以采用启发式的教学方式使教学进一步深入，充分调动学生学习的积极性，提高学生的自学能力和独立思考问题的能力.

例如，在讲授第二类Stirling数和第一类Stirling数时，因为二者是对偶的概念，先详细给出第二类Stirling数的定义，接着介绍它的递推公式及其详细证明，最后给出第二类Stirling数的组合意义.利用反演和对偶的思想，关于第一类Stirling数的定义、递推公式和组合意义，可以留给学生自己去证明.教师可采取上课提问的方式，这样既可以调动学生的主动性，也可以加深学生对两类Stirling数的比较与理解.

除此之外，对于重要的原理和方法，可以给出很多例子让学生练习.教师可以首先给出一个典型的例子加以详细介绍，然后找学生当堂练习一些类似的题目，这样既活跃了课堂气氛，又调动了学生学习的主动性，并且还能查漏补缺，从而达到最好的教学效果.

2.3 提高学生发现问题的能力

要提高学生学习的主动积极性，就必须让学生自己想出一些问题并试着解决它.给学生一个好问题，不如教会学生如何发现问题.在讲解组合数学中的原理、模型及其思想方法时，应该经常提醒学生发散自己的思维，去建立一个新的概念或模型并研究其性质.当然,这种发散不是漫无边际的发散，通常是基于原有概念(模型)的推广或者迁移.

以排列组合为例，n元集S的r-排列是指具有n个元素的集合S中r个元素的有序安排方式数，其中n个元素是完全不重复的.我们可以把集合的排列进行推广，引导学生考虑多重集合的r排列.首先，给出多重集S的定义，即集合S中每一个元素都有一个重数，例如S={2·a，3·b，5·c}表示集合S由2个a，3个b和5个c组成.然后，让学生思考重数无限的多重集的排列和重数有限的多重集的排列.在讲授组合数学的过程中，当讲述完一个概念或者模型时，鼓励大家提出改进模型的办法，并提醒大家注意两个原则——合理性和可行性.教师在讲解的过程中一定要引导学生采用推广或者迁移的方式独立地提出新的问题，能够提出一个好的问题也是独立科学研究能力的象征，对培养学生的数学素养大有裨益.

2.4 培养学生解决问题的能力

尽管如前所述，组合数学解题的具体方法是灵活的、离散的与不可模仿的，但我们还是可以在教学过程中有意识地训练学生的宏观证明能力.通常来说，解决组合数学问题有贡献法、数学归纳法、容斥原理、鸽笼原理、母函数法和二项式(多项式)定理等几种基本方法，有时需要结合使用，下面举例介绍.

贡献法适用于证明计数恒等式.首先选定一个特殊的元素x，然后分别分析等式的左端和右端，看看两端对这个事先选定好的元素的统计次数是否一样多，如果一样多则原计数恒等式得证.贡献法在组合数学的证明中应用广泛，起到了不可替代的作用.巧妙运用贡献法，可给出容斥原理的完美证明.

例5S中不具有任何一个性质的元素数目为：

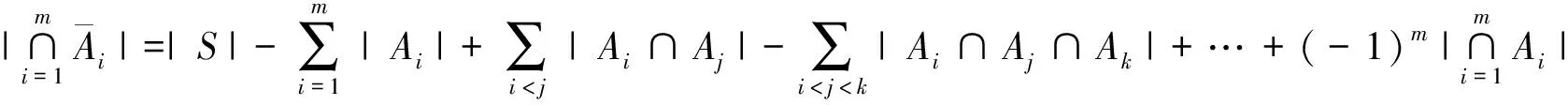
证明：设任意元素xS,它恰有m个性质中的n个性质(0≤n≤m).若n=0,则上式两端对它的计算次数都是1；若n≥1,则x在左端计数0次，而在右端的计数为上述等式成立.

上面例子给出了容斥原理的简单证明，可以发现该原理虽然重要，但是它的内容和证明并不复杂，也不难理解.最重要的是，如何利用这个原理来解决更多的数学问题以及怎样才能恰如其分地运用它，这就需要一种解决数学问题的综合品质.

3 结语

以上组合数学课程教学中的引入和展开方式适用于各个层次的数学课程，教师要关注和重视这些课程教学中的技巧，充分调动学生课堂学习的积极性，倾听他们的想法，使学生在交流互动中增强数学技能.

参考文献：

[1] Brualdi R A. Introductory Combinatorics[M].Beijing:China Machine Press,2009.

[2] Cameron P J.Combinatorics Topics, Techniques, Algorithms[M].Beijing:Posts Telecom Press,2009.

[3] 卢开澄，卢华明.组合数学[M].4版.北京：清华大学出版社，2006.