玻璃纤维纱线的力学性能测试研究
朱进忠,陈建伟
(河南工程学院 纺织工程系,河南 郑州 450007)
玻璃纤维是一种性能优异的无机非金属材料,具有不燃、耐高温、抗拉强度高、电绝缘好、化学稳定性好等优良特性,已被广泛地应用在交通运输、石油化工、电子电器、航空航天、建筑、环保、机械、核能、兵器等领域[1-2].为了充分发挥玻璃纤维的优良特性,许多专家学者做了大量研究.有学者做了玻璃纤维摩擦性能方面的研究[3],有的做了玻璃纤维纱线力学性能损伤的研究[4-5],有的做了玻璃纤维纱线强力与捻度、捻系数关系的研究[6-7],还有的从弯曲拉伸与直拉中探讨玻璃纤维纱线的编织性能与工艺性能[8-9],但很少有研究玻璃纤维纱线加捻对断裂伸长率的影响及测试拉伸速度、有效长度对玻璃纤维纱线力学性能测试结果影响的.本研究做了这方面的相关研究,并给出了有关分析结论.
1 测试条件对力学性能测试结果的影响
1.1 实验方法
实验材料是35 tex×2双股玻璃纤维纱线,主要实验仪器是HD026N型电子强力仪.
不同拉伸速度实验:在有效长度为300 mm的条件下,测试4组不同拉伸速度纱样的强伸度与断裂功,每组纱样取3次的平均值,绘出与拉伸速度的回归关系图,拉伸速度分别取200 mm/min、300 mm/min、400 mm/min和500 mm/min.
不同有效长度实验:在拉伸速度为200 mm/min条件下,测试4组不同有效长度纱样的强伸度与断裂功,每组纱样取3次的平均值,绘出与有效长度的回归关系图,有效长度分别取200 mm、300 mm、400 mm和500 mm.
1.2 实验结果与分析
1.2.1 拉伸速度的影响
玻璃纤维纱线不同拉伸速度的测试结果如表1所示.
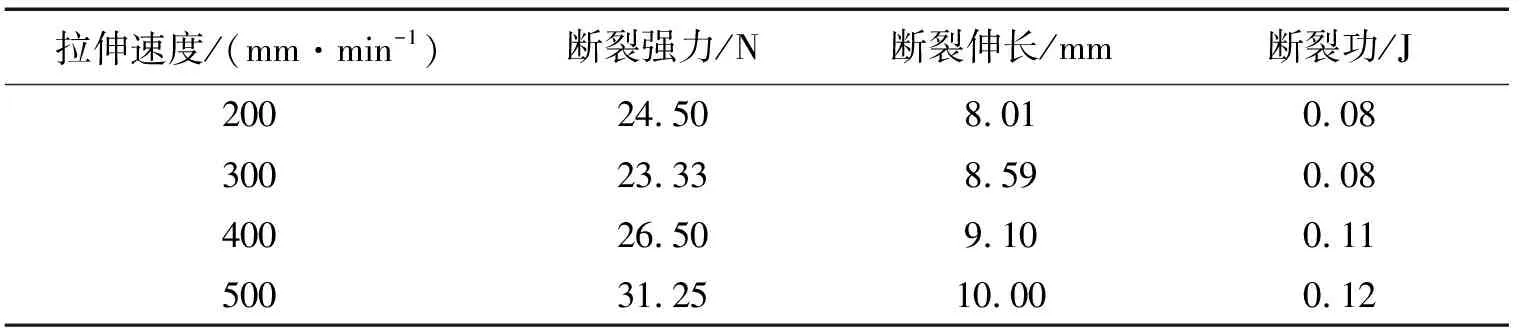
表1 不同拉伸速度的测试结果Tab.1 Tensile test results of different speeds
纱样的强伸度、断裂功与拉伸速度的关系如图1~图3所示.应用origin8.0数学分析软件对数据进行拟合,得到纱样的回归曲线见图1~图3.其中,断裂强度对拉伸速度的回归方程为:
y= 0.023 4x+0.32,
(1)
相关系数的平方R2=0.75,根据显著水平α= 0.05和自由度v=n-2-1 = 8,查相关系数临界值表得γ0.05,8=0.631 9,这表明在显著水平α= 0.05的条件下,回归方程(1)相关性显著.

图1 断裂强度-拉伸速度关系Fig.1 Breaking strength-tensile rate
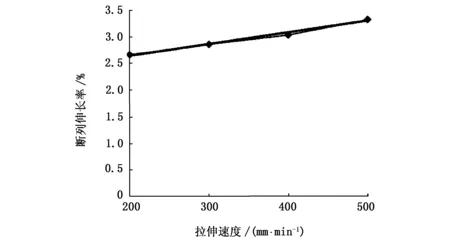
图2 断裂伸长率-拉伸速度关系Fig.2 Elongation at break-tensile rate

图3 断裂功-拉伸速度关系Fig.3 Broken power-tensile rate
断裂伸长率对拉伸速度的回归方程为:
y=0.006 5x+2.67,
(2)
相关系数的平方R2=0.983 1,根据显著水平α=0.05和自由度v=n-2-1 = 8,查相关系数临界值表得γ0.05,8=0.631 9,这表明在显著水平α= 0.05的条件下,回归方程(2)相关性显著.
断裂功对拉伸速度的回归方程为:
y=0.000 2x+0.045,
(3)
相关系数的平方R2=0.882 4,根据显著水平α=0.05和自由度v=n-2-1 = 8,查相关系数临界值表得γ0.05,8=0.631 9,这表明在显著水平α= 0.05的条件下,回归方程(3)相关性显著.
可以看出,测试拉伸速度对玻璃纤维纱线的强伸度和断裂功的影响比较显著,随着测试拉伸速度的增加,强伸度和断裂功均有增大的趋势且几乎呈线性相关.这个现象产生的原因主要有二:①玻璃纤维虽不是高分子材料,但也可以看成具有近乎高分子材料的蠕变松弛现象,会产生力学性能时间效应;②玻璃纤维经加捻而成纱线,在外力的作用下纱线中的玻璃纤维会产生摩擦作用.纱样受拉时,纱线结构要产生变化,纱线中的玻璃纤维就要克服加捻引起的摩擦作用.在克服这一摩擦作用时会产生时间效应,即受拉时间长了,摩擦作用被克服而表现为拉伸力小;受拉时间短了,摩擦作用未被克服而表现为拉伸力大,这样就会出现随着测试拉伸速度的增加纱线受拉时间变短而强力增大的现象.
由于拉伸速度对玻璃纤维纱线强伸度和断裂功测试的影响比较大,所以在测试玻璃纤维纱线力学性能时应考虑消除拉伸速度所产生的影响,即采用国家标准统一规定的拉伸速度.
1.2.2 有效长度的影响
不同有效长度的玻璃纤维纱线测试结果如表2所示.

表2 不同有效长度的纱线测试结果Tab.2 Effective length of the test results of different yarns
纱样的强伸度、断裂功与有效长度的关系如图4~图6所示.应用origin8.0数学分析软件对数据进行拟合,得到纱样的回归曲线见图4~图6.其中,断裂强度对有效长度的回归方程为:
y= -0.005 8x+ 0.339 3,
(4)
相关系数的平方R2= 0.821 2,根据显著水平α= 0.05和自由度v=n-2-1 = 8,查相关系数临界值表得γ0.05,8=0.631 9,这表明在显著水平α= 0.05的条件下,回归方程(4)相关性显著.用F检验法对回归方程的显著性进行检验,回归方程显著.
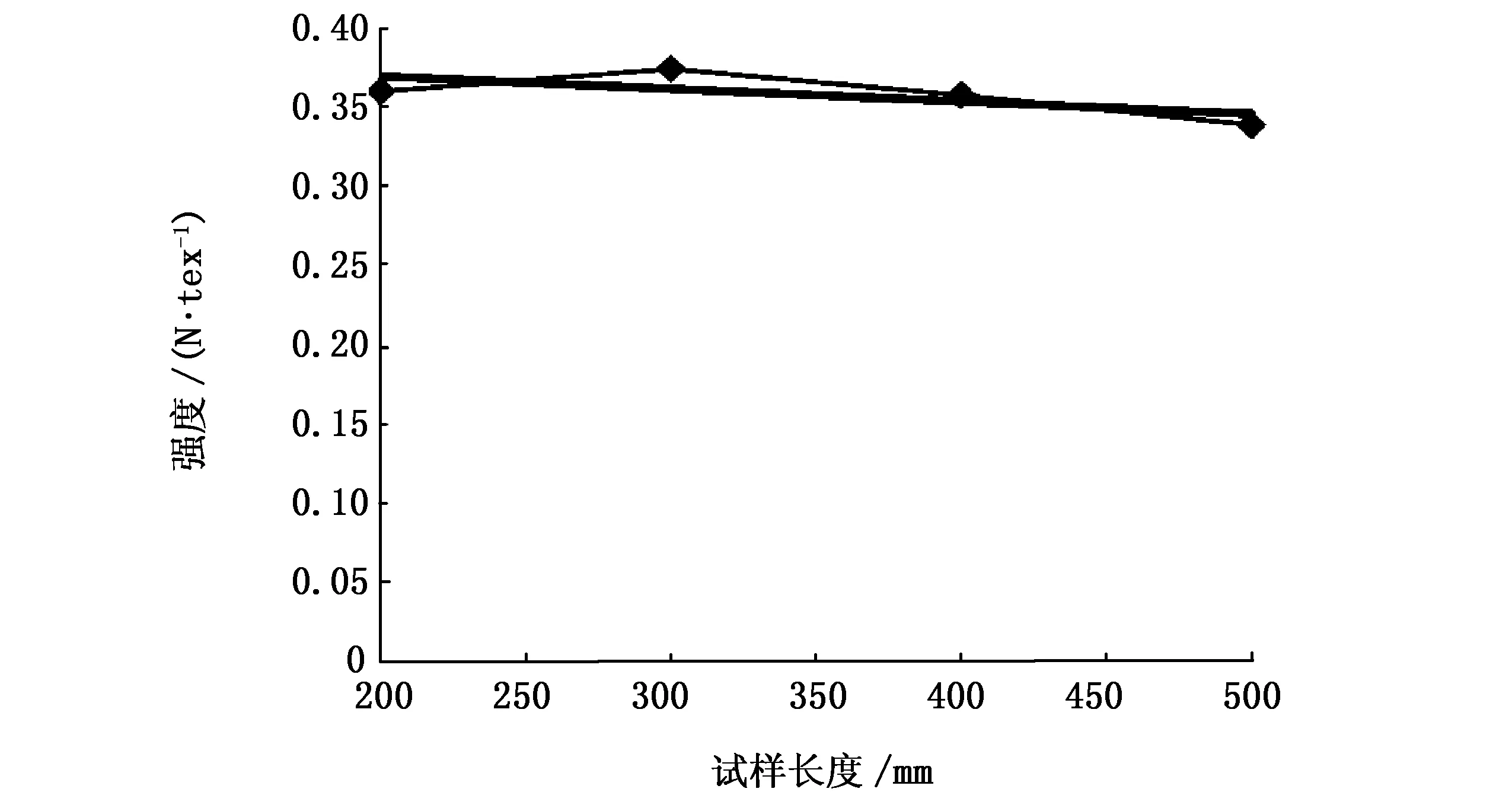
图4 断裂强度-有效长度关系Fig.4 Breaking strength-effective length

图5 断裂伸长率-有效长度关系Fig.5 Elongation at break-effective length

图6 断裂功-有效长度关系Fig.6 Broken power-effective length
断裂伸长率对有效长度的回归方程为:
y= -0.001 5x+2.655,
(5)
相关系数的平方R2=0.785 2,根据显著水平α=0.05和自由度v=n-2-1 = 8,查相关系数临界值表得γ0.05,8=0.631 9,这表明在显著水平α= 0.05的条件下,回归方程(5)相关性显著.
断裂功对有效长度的回归方程为:
y=0.000 09x+0.051,
(6)
相关系数的平方R2=0.852 6,根据显著水平α=0.05和自由度v=n-2-1 = 8,查相关系数临界值表得γ0.05,8=0.631 9,这表明在显著水平α= 0.05的条件下,回归方程(6)相关性显著.
可以看出,测试有效长度对玻璃纤维纱线的强伸度和断裂功测试的影响也比较显著,随着测试有效长度的增加,强伸度和断裂功均有降低的趋势且几乎呈线性相关.这个现象产生的原因可做如下解释,即纱线受力时,断裂总发生在强力最弱处,纱线强力是最弱处所能承受的外力.测试有效长度越长,纱线强力不匀的地方越多,纱线强力最弱处被测到的机会越多,纱线强力就越小.同样,因为有效长度对玻璃纤维纱线力学性能测试的影响比较显著,在测试玻璃纤维纱线的力学性能时,应考虑有效长度的影响,以免对实验数据的准确性造成干扰.
2 玻璃纤维纱线强伸度与捻度的关系
2.1 实验方法
实验材料是35 tex×2玻璃纤维纱线,主要的实验仪器是Y331LN型捻度仪、HD026N型电子强力仪和FA2004型电子天平.
依照国家标准[10-12],先测出玻璃纤维纱线的捻度,再对其进行捻度追加,分别自制出10组不同捻度的纱样.然后,在同等条件下,分别测试每组纱样的线密度和强伸度,测试有效长度为200 mm.
2.2 实验结果与分析
2.2.1 强度与捻度的关系
35 tex×2玻璃纤维纱线测试的结果如表3所示.从表3中可以看出,追加捻度后的试样不但强力和伸长发生了变化,线密度也发生了变化,所以计算纱线强度时要考虑线密度的变化.

表3 35 tex×2纱线强伸度测试结果Tab.3 35 tex×2 yarn strength and elongation tests

图7 35 tex×2纱线强度-捻度关系Fig.7 35 tex×2 yarn strength-twist
纱线强度与捻度关系所图7所示.应用origin8.0数学分析软件对数据进行拟合,得到玻璃纤维纱线强度对捻度的回归方程,进行了相关显著性检验,结果如表4所示.
从图7可以看出,纱线的强度随着捻度的增加而增加,当增加到一定值时,强度又随着捻度的增加而降低.这主要是由于加捻后纤维的倾斜使其所能承受的轴向分力有所减少,而且加捻过程中使纱线中的纤维产生预应力,致使纱线受力时纤维再承受外力的能力降低.当捻度增加到一定程度时,纱线强力达到最大值,此后捻度增加但纱线强力反而降低,其强度最大时的捻度就是临界捻度.按回归方程计算出临界捻度及相应临界捻系数、最大强度与相应最大强力,如表4所示.

表4 回归结果分析Tab.4 Regression analysis
为了进行比较,将文献[7]中的50 tex×3玻璃纤维纱线与22 tex×3玻璃纤维纱线重新测试后的结果分析也一并放入表4中,其纱线强度-捻度关系如图8与图9所示.可以看出,3种玻璃纤维纱线的临界捻度、临界捻系数、最大强度与最大强力各不相同,原因是3种玻璃纤维纱线的线密度及构成不同,即随着线密度及纱线构成的不同,玻璃纤维纱线的临界值各不相同,在设计生产中应引起注意.

图8 50 tex×3纱线强度-捻度关系Fig.8 50 tex×3 yarn strength-twist diagram
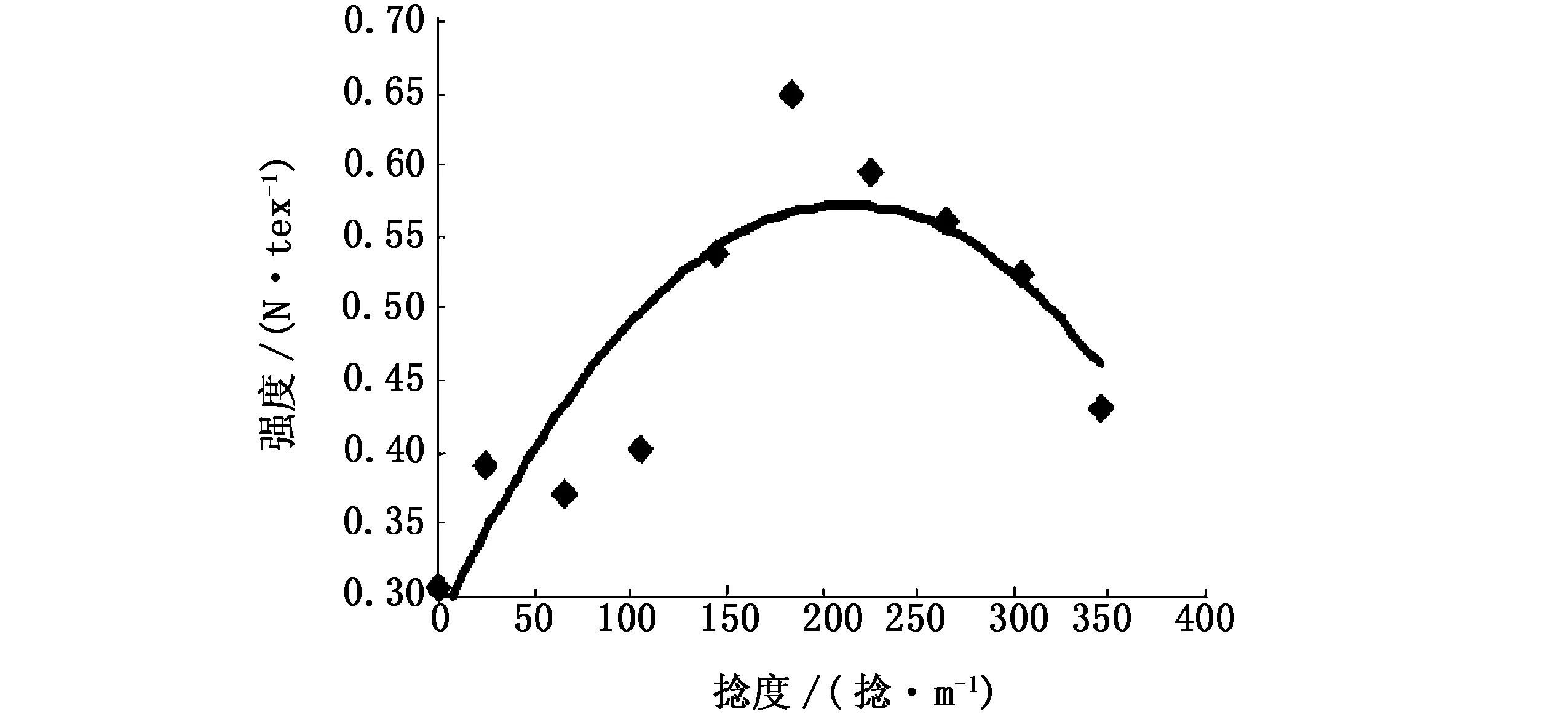
图9 22 tex×3纱线强度-捻度关系Fig.9 22 tex×3 yarn strength-twist diagram

2.2.2 断裂伸长率与捻度的关系

图10 35 tex×2断裂伸长率-捻度关系Fig.10 35 tex×2 elongation at break-twist diagram
35 tex×2玻璃纤维纱线的断裂伸长率与捻度的关系如图10所示.应用origin8.0数学分析软件对数据进行拟合,得到35 tex×2玻璃纤维纱线断裂伸长率对捻度的回归方程为:
y= 0.010 4x+ 3.225,
(7)
相关系数的平方R2=0.895 7,根据显著水平α=0.05和自由度v=n-2-1 = 8,查相关系数临界值表得γ0.05,8=0.631 9,这表明在显著水平α= 0.05的条件下,回归方程相关性显著.
由图10可以看出,35 tex×2玻璃纤维纱线的断裂伸长率也随着捻度的增加而几乎呈线性增加.这是因为玻璃纤维纱线拉伸断裂时所产生的伸长是由两部分组成的,一是纱线中的单丝因受外力作用产生的伸长;二是纱线的捻回角和直径变小而产生的伸长.在拉伸断裂的过程中,随着捻系数的增加,由捻回角变小和直径变小而产生的伸长增加了.
3 结论
对玻璃纤维纱线的力学性能进行了研究,重点分析了拉伸速度和有效长度对玻璃纤维纱线力学性能测试的影响以及捻度对玻璃纤维纱线强伸度的影响.通过实验并进行理论分析之后,得出以下结论:
(1)在测试玻璃纤维纱线的力学性能时,拉伸速度和有效长度对强伸度、断裂功等测试结果有显著的影响,应采用国家标准统一规定的测试拉伸速度和有效长度,以免对实验数据的准确性造成干扰.
(2)玻璃纤维纱线的强度随着捻度的增加而加大,有临界值.随着纱线线密度及构成的不同,玻璃纤维纱线的临界捻度、临界捻系数、最大强度与最大强力等临界值各不相同,在设计生产中应引起注意.
(3)玻璃纤维纱线的断裂伸长率随着捻度的增加而几乎呈线性增加.
参考文献:
[1] 刘新年,张红林,贺祯,等.玻璃纤维新的应用领域及发展[J].陕西科技大学学报,2009,5(27):169-171,180.
[2] Kaynak C,Arikan A,Tincer T. Flexibility improvement of short glass fiber reinforced epoxy by using a liquid elastomer [J].Polymer,2003,44(8):24-27.
[3] 刘晓明,蒋金华,陈南梁,等.玻璃纤维纱线的摩擦性能及其影响因素的研究[J].产业用纺织品,2008(2):28-32.
[4] 蒋金华,刘晓明,陈南梁.预型加工过程中玻璃纤维纱线损伤原因的试验分析[J].东华大学学报:自然科学版,2007,6(33):812-815.
[5] 朱进忠,苏玉恒,严广松.玻璃纤维纱线力学性质损伤的测试分析[J].河南工程学院学报:自然科学版,2011,23(1):11-14.
[6] 刘明.玻璃纤维纱线的最佳强力捻系数研究[J].上海纺织科技,2009,37(9):26-27,57.
[7] 朱进忠,苏玉恒.玻璃纤维纱线强力与捻度的关系[J].河南工程学院学报:自然科学版,2010,22(1):8-10.
[8] 龙海如.玻璃纤维横机针织物编织工艺探讨[J].针织工业,2001,17(6):37-39.
[9] Hu H,Zhu M. A study of the degree of breakage of glass filament yarns during the weft knitting process[J].AUTEX Research Journal,2005,5(3):141-148.
[10] GB/T 7690.1—2001.增强材料 纱线试验方法 第1部分:线密度的测定[S].2001.
[11] GB/T 7690.2—2001.增强材料 纱线试验方法 第2部分:捻度的测定[S].2001.
[12] GB/T 7690.3—2001.增强材料 纱线试验方法 第3部分:玻璃纤维断裂强力和断裂伸长的测定[S].2001.

