对Engheta双负介质谐振腔的研究
邓跃龙,蒋练军 贾 平,熊翠秀,徐志锋
(1.益阳医学高等专科学校公共课部,中国 益阳 413000;2.湖南城市学院物理与电信工程系,中国 益阳 413000)
1968年Veselago[1]从理论上研究、预测了介电常数ε和磁导率μ同时为负的双负材料,电磁波在其中传播时,波矢k、电场E和磁场H方向的关系满足左手定律,因此称之为“左手材料” .电磁波在双负材料中传播时有很多奇异的性质,如作为辐射天线的底板,相比传统的天线可以提高天线的辐射效率,利用双负材料设计的亚波长谐振腔可突破传统金属谐振腔的尺寸限制,一个很小的谐振腔可以束缚住波长很大的电磁波.负折射现象是人们以前从未观察到的一种崭新现象,新的发现往往会带来很大的应用前景.在其被提出后的30年里,左手介质这一具有颠覆性的概念却一直处于无人问津的尴尬境地,直到Smith等第一次实际合成出这种自然界并不存在的介质,它的超常规电磁特性,如:凋落波聚焦特性、相位补偿效应等,再次引发了人们的研究热潮.
目前,对于这种材料的大量研究工作致力于利用LHM的反常电磁特性来缩小微波器件体积或占用面积,2002年Engheta[2]等从理论上提出了一种谐振腔结构,它由LHM和普通介质组成的一维小型化谐振结构[3-8].
Engheta理论研究表明,将左手介质的反向波效应和传统介质的前向波效应相结合设计出的谐振腔的物理尺寸不再受制于谐振频率,而是取决于左手介质和传统介质的本构关系参数的比值,其中左手介质相当于一个相位补偿器,左手介质作为相位补偿器,在微带无线小型化方面具有巨大的应用潜力.因此,进一步探讨Engheta的谐振腔理论,具有非常重要的理论和实际意义.
本文将针对“Engheta”双负谐振腔模型进行理论分析,考虑普通介质层和双负介质层界面发生反射时谐振腔的共振条件和稳定性问题,讨论普通介质层和双负介质层的阻抗不匹配时一维亚波长谐振腔的稳定性问题.
1 双负介质谐振腔的物理模型与理论
1.1 Engheta谐振腔模型
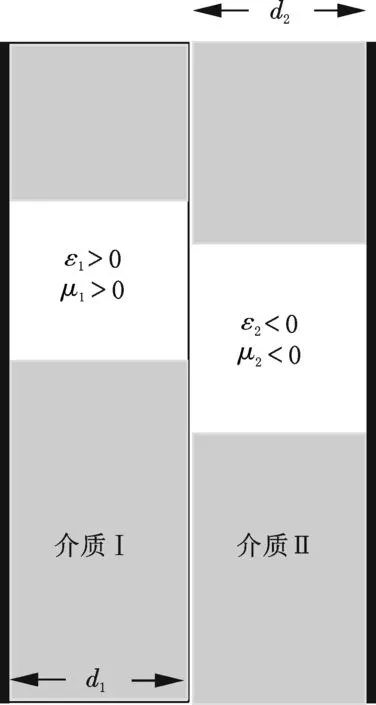
图1 Engheta所建议的一维亚波长谐振腔的结构
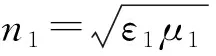
1.2 Engheta谐振腔理论分析
图1所示结构的谐振方程为

(1)
式中k0为自由空间的波数;n1和n2分别为介质Ⅰ和介质Ⅱ的折射率;d1和d2分别为介质Ⅰ和介质Ⅱ的长度.谐振方程(1)在亚波长条件下具有两组物理解,一组是当n1和n2为符号相同的实数, 而k1和k2为符号相反的实数时,可以使谐振方程(1)在亚波长条件下得到满足,特别是当n1=n2,并且k1d1=-k2d2时, 谐振方程(1)恰巧满足.该组解代表的物理意义是图1所示的谐振结构中介质Ⅰ为普通介质,介质Ⅱ为LHM,可以看出这正是Engheta谐振结构的理论基础.电磁波在图1所示的相邻连续的左手介质和右手介质中传播时,由于相位相反,左手介质会对右手介质进行相位补偿[9].所以,只要在相邻两介质层中相位变化的模值相等,电磁波在通过图1所示的双层介质后,相位变化将完全抵消.这使得该谐振腔系统的谐振方程(1)不依赖于两介质层的各自厚度,而直接取决于它们的比值.所以, 该谐振腔可以保持在亚波长宽度,甚至还可以大幅度降低.而且如果满足

图2 AB结构的谐振腔结构示意图
n1k0d1=-n2k0d2,
(2)

(3)
则谐振方程(1)成立[10].而且,由于(1)式等号两端的波矢量被直接消去, 谐振方程(1)将与频率无关.该谐振腔系统可在任何频率下谐振.
方程(1)的另一组解是当k1和k2为符号相同的虚数,而n1和n2为符号相反的虚数时,同样可以使谐振方程(1)在亚波长条件下得到满足,特别是当n1=-n2,并且k1d1=k2d2时,谐振方程(1)恰巧满足[11].该组解代表的物理意义是图2所示的谐振结构中介质Ⅰ为负磁导率介质,介质Ⅱ为负介电常数介质.我们通过进一步分析发现,除了上述的两组物理解之外,还有两组非常具有实际物理意义的近似解.为了清晰地解释这两组物理解的由来,首先需要更为深入地研究负介电常数介质和负磁导率介质中波阻抗与相位常数之间的关系.
对于负磁导率介质,因为它的磁导率μm<0,介电常数εm>0,所以负磁导率介质的相位常数可以写成如下形式
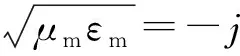
(4)
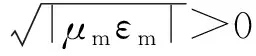

(5)
其中Xm=αm/εm.由此可以看到,负磁导率介质的波阻抗与相位常数的乘积为负实数,对于负介电常数介质,因为它的磁导率μe>0,介电常数εe<0,所以负介电常数介质的相位常数可以写成

(6)

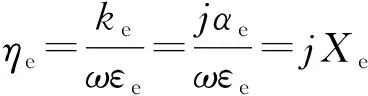
(7)
其中Xe=αeεe>0,由此可以看到,负介电常数的波阻抗与相位常数的乘积为正实数.
另一方面,当|k1d1|,|k2d2|≪1,(1)式可以简化为
n1k1d1+n2k2d2=0.
(8)
由(8)式可知,当介质Ⅰ为普通介质,介质Ⅱ为负磁导率介质时,n1k1d1为大于零的实数,而n2k2d2=-Xmαmd2则为小于零的实数.此时,如果参数选取适当完全可以在亚波长条件下满足(8)式给出的谐振方程,特别是当ε1=ε2=ε0,μ1=-μ2=μ0并且d1=d2时,(8)式恰能满足.同样,介质Ⅰ为LHM,介质Ⅱ为负介电常数介质时,n1k1d1为小于零的实数,而n2k2d2=-Xeαed2则为大于零的实数,此时在参数选取适当的情况下也完全可以在亚波长条件下满足(8)式给出的谐振方程,特别是当ε1=ε2=-ε0,μ1=-μ2=-μ0并且d1=d2时,(8)式恰巧得到满足.另外,通过更深层次的理论推导表明,对于所有基于LHM的一维小型化谐振结构,即使当LHM为各向异性时(8)式仍然能够在亚波长条件下成立[3].以上述的LHM与负介电常数介质交叠谐振结构为例,当LHM的本构参数张量为

(9a)
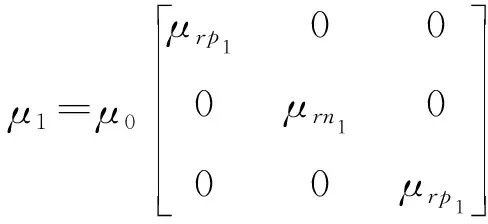
(9b)
负介电常数介质的本构参数张量为
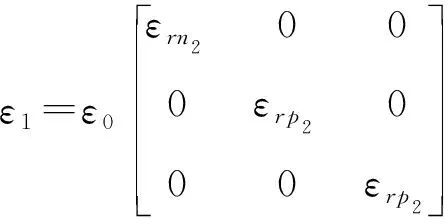
(10a)
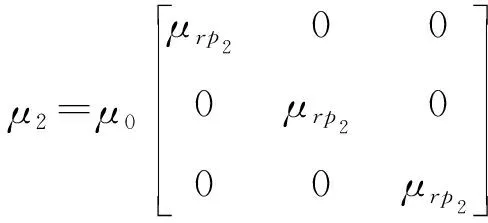
(10b)
时,(8)式给出的谐振方程仍然能够在亚波长条件下得到满足,并且谐振模式与各向同性LHM与负介电常数介质交叠结构的谐振模式相类似.
2 双负介质谐振腔的共振条件与稳定性分析
上面我们分析了Engheta双负介质谐振腔的物理模型与相关理论,下面我们进一步来探讨Engheta双负介质一维亚波长谐振腔的共振条件和稳定性方面的问题[12].
2.1 界面处发生反射时的共振条件
既然当电磁波垂直通过普通介质层和双负介质层的界面时没有发生相位变化(这两个介质层都是无损的)[13],那么根据简单的光线分析方法我们会猜测只要满足
n1d1+n2d2=0,
(11)
谐振腔就可以实现共振.我们称(11)式为光线猜测.由(11)式可知谐振腔共振对普通介质层和双负介质层的厚度比有要求,而对它们的总厚度d1+d2没有什么要求,因此只要普通介质层和双负介质层的厚度比满足(11)式,谐振腔可以做到在厚度任意薄的情况下实现共振.但以上这种光线分析没有考虑普通介质层和双负介质层界面上的反射,实际上当这两层介质的阻抗不匹配时,虽然谐振腔仍然可以具有次波长厚度,但已不满足(11)式,下面将给出一个例子.
由Maxwall方程和边界条件我们可以得到以下的共振条件
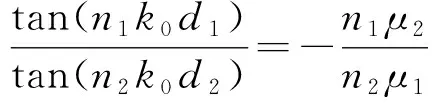
(12)
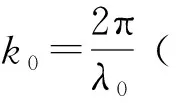
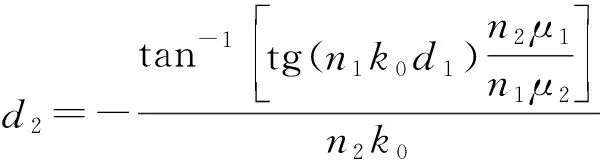
(13)

2.2 两层介质阻抗不匹配时谐振腔的稳定性
从上述可知,光线分析也无法确定一维次波长谐振腔的稳定性.一维次波长谐振腔是不稳定的,下面我们以普通介质层和双负介质层的阻抗稍微不匹配的一维次波长谐振腔为例对此进行说明.

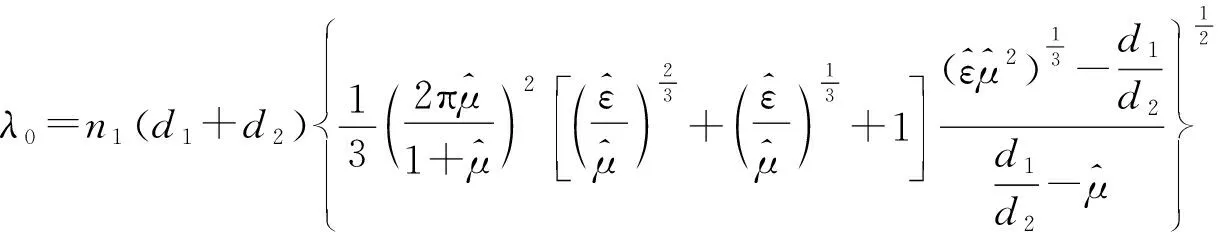
(14)
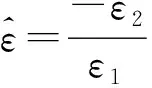
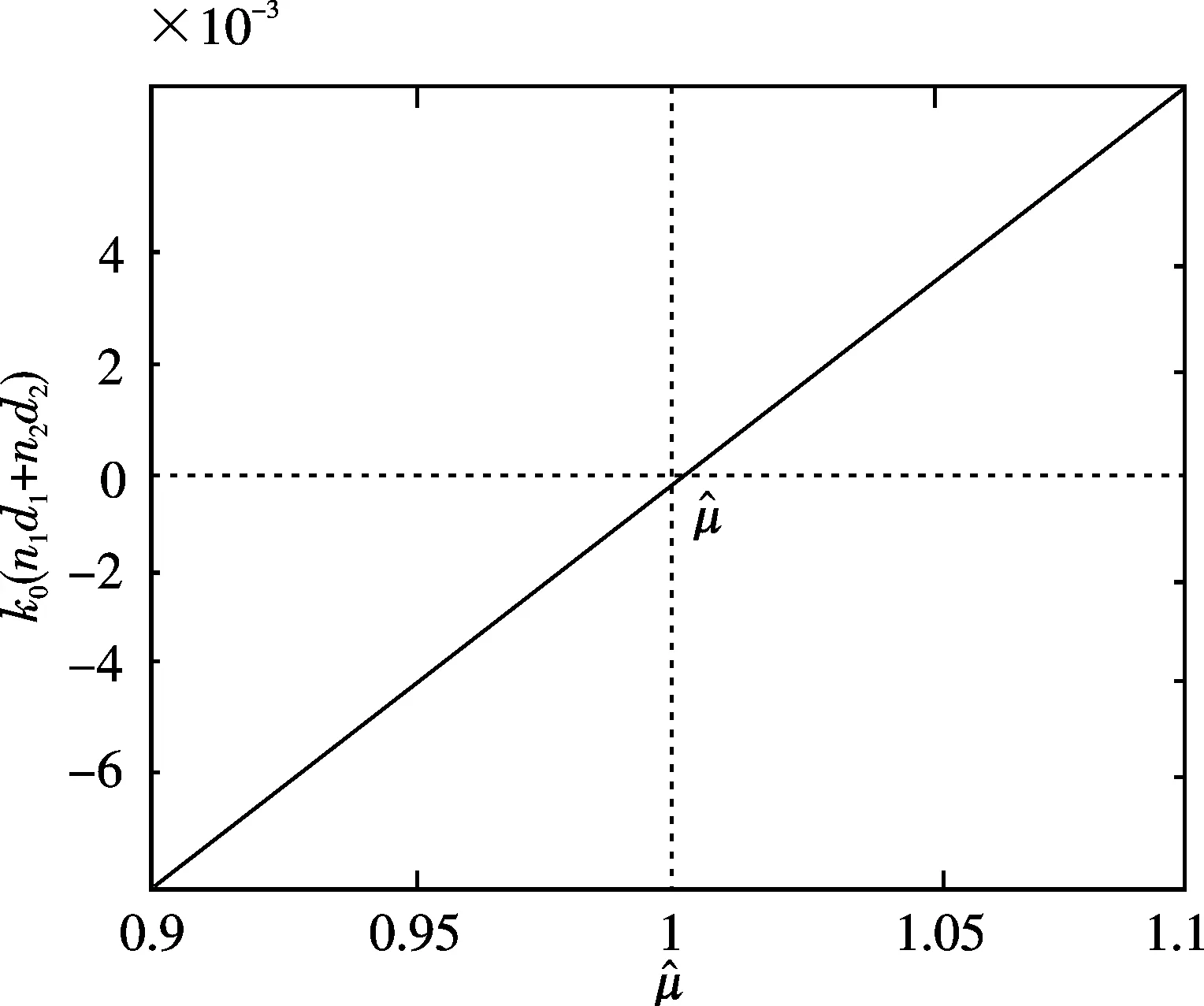
,ε1=μ1=1,n2=-1图3 一维亚波长谐振腔共振时k0n1d1+n2d2和的关系
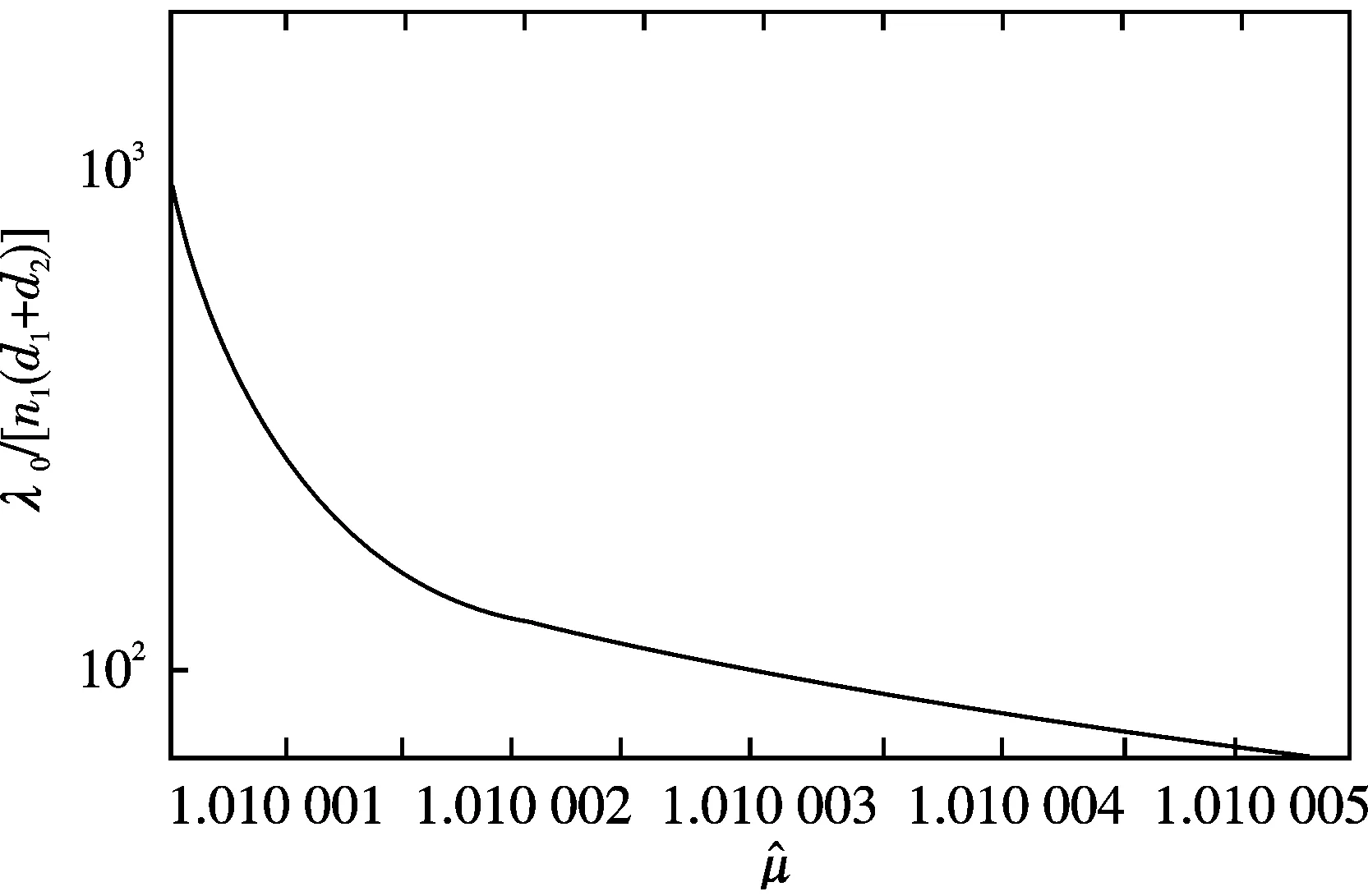
,.01图4 一维亚波长谐振腔共振时与的关系
3 结论
参考文献:
[1] VESELAGO V G. The electrodynamics of substance with simultaneously negative values ofεandμ[J] .Phys Usp,1968,10(4):509-514.
[2] ENGHETA N. An idea for thin subwavelength cavity resonators using metamaterials with negative permittivity and permeability [J].IEEE Antennas Wireless Propag Lett,2002,1(1):10-13.
[3] 吴 群,孟繁义,傅佳辉,等.基于双负介质与负介电常数介质交叠结构的谐振腔研究[J].物理学报, 2008,57(4):2179-2185.
[4] ALU A, ENGHETA N. Physical insight into the “growing” evanescent fields of double-negative metamaterial lenses using their circuit equivalence [J]. IEEE Trans Antennas Propag Lett, 2006,54(1):268-272.
[5] SHEN L F, HE S L, XIAO S S. Stability and quality factor of a one-dimensional subwavelength cavity resonator containing a left-handed material[J].Phys Rev B,2004,69(11):111-116.
[6] WU L, HE S L, SHEN L F. Band structure for one-dimensional, photonic crystal containing left-handed, materials [J]. Phys Rev B, 2003, 23(7):35-40.
[7] SHADRIVOV I V, SUKHORUKOV A A, KIVSHAR Y S. Complete band gaps in one-dimensional left-handed periodic stuctures[J].Phys Rev Lett,2005, 95(5):503-508.
[8] SHADRIVOV I V, SUKHORUKOV A A, KIVSHAR Y S. One-dimensional periodic stuctures with complete spectral gap [J]. Proc SPIE, 2005,60(8):54-58.
[9] PIMENOV A, LOIDL A, PRZYSLUPSKI P,etal. Negative refraction in ferromagnet-superconductor superlattices[J]. Phys Rev Lett,2005,95(24):2470-2472.
[10] 杨 锐,谢拥军,王 鹏,等.含有左手介质双层基底的亚波长谐振腔微带天线研究[J].物理学报,2007,56(8):4504-4508.
[11] HE Y X, HE P, VINCENT G H,etal. Role of ferrites in negative index metamaterials [J]. IEEE Trans Mag, 2006,42(10):2852-2858.
[12] 金 毅.负折射介质特性与应用的若干研究[D].浙江:浙江大学信息学院,2006.
[13] 邓跃龙,蒋练军,贾 平,等.基于亚铁磁材料-YIG的负折射率特异材料的设计及电磁特性研究[J].湖南师范大学自然科学学报,2011,34(3):27-31.

