由星补刻画的一类广义线图
袁名焱,罗秋红,汤自凯
(湖南师范大学数学与计算机科学学院, 中国 长沙 410081)
设G为简单图, 记G的顶点集为V(G)={1,2,…,n},G的邻接矩阵为A=(aij), 其中
矩阵A的特征值称为图G的特征值.

1 一些引理
引理1[3](重构定理) 若图G的邻接矩阵为
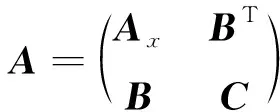
(1)
其中Ax表示图G的导出子图X的邻接矩阵, 则X是图G关于特征值μ的星集当且仅当μ不是矩阵C的特征值, 且
μI-Ax=BT(μI-C)-1B.
(2)
给定一个图H, 假设U为顶点集V(H)的子集, 且顶点v∉V(H). 把顶点v和顶点集U中的每个顶点都相连, 从而得到图H(U), 如果μ不是图H的特征值, 却是图H(U)的特征值, 我们称U是特征值μ的好集. 可知星集里任何一顶点vi在星补H的邻集Ui都是好集.
鸡尾酒会图C(Pn)是完全图K2n去掉一个由n条边组成的完美匹配,C(P0)表示空图.
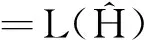
由图谱理论[5]可知广义线图的最小特征值λmin≥-2, 而且除了广义线图之外只有有限个连通图的最小特征值也大于等于-2, 这类图称之为例外图, 例外图最多有36个顶点[6-7].关于星补图的其他相关文献请参考[8~12].
注1假设U是特征值μ的好集, 即μ是图H(U)的特征值, 如果λmin(H)>μ, 由插值定理知μ是图H(U)的最小特征值.
注2假设图G的λmin(G)=-2, 图G′为图G的导出子图, 由插值定理[4]知:λmin(G′) ≥-2, 即不存在图G′为图G的导出子图使得λmin(G′)<-2, 我们把这种方法称为禁忌子图技巧.
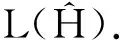
已知Smith图是一类最大特征值为2的连通简单图,见图1,图T1(n),T2(n)中n表示图的阶数.
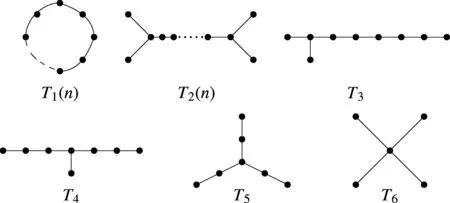
图1 Smith图
推论1[8]若Smith图不为奇圈, 则最小特征值为-2.
我们称Smith图的连通导出子图为简化Smith图.
推论2[8]任何简化Smith图的最小特征值大于-2.
引理2[8]任何一个异于图C3,C5,C7的Smith图G加一条悬挂边(或加多条悬挂边)得到图H,则λmin(H)<-2.
引理3[4]假设一个连通非二部图H有n个顶点,m条边, 则线图L(H)的特征值-2的重数K=2m-n. 当H为连通二部图时,K=m-n+1.
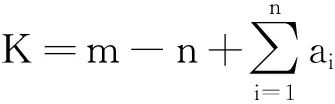
2 Ct+2sK1作为特征值-2的星补
设图G是以H=Ct+2sK1为特征值-2的星补的连通图,C表示图H的邻接矩阵,X表示特征值-2的星集,v为星集里任意一顶点, 由引理1的(2)式得:bTMb=8, 其中b为顶点v的刻画向量,M=4(2I+C)-1. 设M=(mij), 则
(3)
令M(S)=bTMb=8, 其中顶点集S表示顶点v在星补H里的邻集, 换句话说,S是顶点v的好集:S={u∈V(H):u~v}, 则M(S)是由顶点集S决定的矩阵M中的主子阵各元素之和. 不妨设S1表示顶点v在圈Ct里的邻集:S1={u∈V(Ct):u~v},S2表示顶点v在孤立点集2sK1里的邻集:S2={u∈V(2sK1):u~v}.
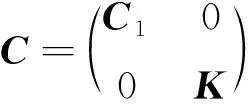
M(S)=M(S1)+M(S2)=8.
(4)
引理5[9]假设t为大于3的奇数,S1表示顶点集V(Ct)的子集,若|S1|为偶数, 不妨设|S1| =2h, 则M(S1)≥4h. 等号成立当且仅当S1是由V(Ct)中的h对相邻的点组成.
引理6当t为大于1的奇数时, 图G是以H=Ct+2sK1作为特征值μ=-2的星补, 则星集X里的顶点v的好集U有以下3类:
1° {qi,qj,qk,ql}(qr∈V(2sK1),r∈{i,j,k,l}),
2° {pi,pi+1,qk,ql}(pr∈V(Ct),r∈{i,i+1})(qw∈V(2sK1),w∈{k;l}),
3° {pi,pi+1,pj,pj+1}(pr∈V(Ct),r∈{i,i+1,j,j+1}).
证由等式(4)知M(S)=M(S1)+M(S2)=8. 假设|S1|为奇数, 由等式(3)知,当i
当h=1时, 不妨设S1={pi,pj}, 其中j>i. 由等式(3)得
(5)
由等式(5), |M(S1)|=4(mod8). 结合等式(4)得M(S1)=M(S2)=4, 且pi,pj为圈Ct上一对相邻的顶点, 即pi,pj可表示为pi,pi+1. 由M(S2)=4得|S2|=2. 不妨设S2={qk,ql}为任意2个孤立顶点,2°得证.
当h=2时, 由引理5得M(S1)≥8. 结合等式(4), 有M(S1)=8, 且|S1|=4是圈Ct上两对相邻的点.不妨设S1={pi,pi+1,pj,pj+1}, 3°得证.
引理7当t为大于1的奇整数时, 设图G是以H=Ct+2sK1为特征值-2的星补的连通图,用X1表示星集X里好集属于类型1°的集合,X2表示星集X里好集属于类型2°的集合,X3表示星集X里好集属于类型3°的集合. 则
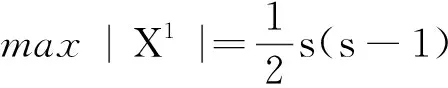
且星补H里的孤立顶点总数为偶数, 即s为非负偶数, 故把星补记成H=Ct+2sK1.
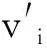
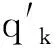
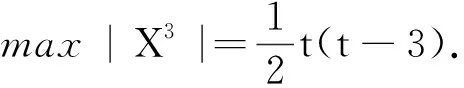
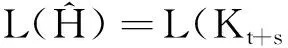
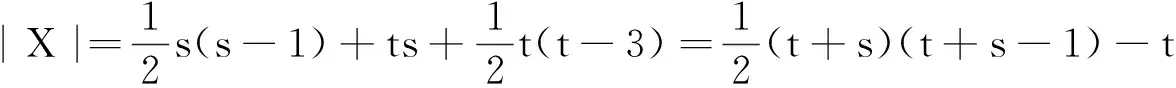
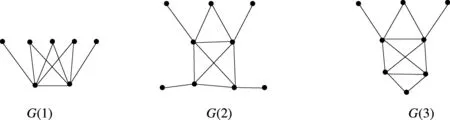
图2 图G(1),G(2),G(3),其中λmin(G(1))=-2.192 58, λmin(G(2))=-2.039 73, λmin(G(3))=-2.166 96.
参考文献:
[1] BELL F K, POWLINSON P. On the multiplicities of graph eigenvalues[J]. Bull London Math Soc, 2003,35(3):401-408.
[2] ROWLINSON P. On multiple eigenvalues of trees[J]. Linear Algebra Appl, 2010,423(11):3007-3011.
[8] BELL F K, SLOBODAN K S. On graphs whose star complement for -2 is a path or a cycle[J]. Linear Algebra Appl, 2004,377:249-265.
[9] BELL F K. Characterizing line graphs by star complements[J]. Linear Algebra Appl, 1999,296(1-3):15-25.
[10] ELLINGHAM M N. Basic subgraphs and graph spectra[J]. AUS J Comb,1993(8):247-265.
[11] ROWLINSON P. Star partitions and regularity in graphs[J]. Linear Algebra Appl, 1995,226-228:247-265.
[12] ROWLINSON P, BELL F K. Graph eigenspace of small codimension[J].Discrete Math, 2000,220:1-3.

