基于GM-GRNN的能源需求预测模型研究

张帆

（湖北汽车工业学院 电气与信息工程学院，湖北 十堰442002）

0 引言

能源是国家经济增长、社会发展的重要物质基础。自改革开放以来，据统计，我国能源消费总量由1978年的5.7亿吨标准煤增长到2011年的32亿吨标准煤，能源消费总量增加了5.6倍。在未来较长的时间内，我国的能源需求量将会继续增长，因此能源供应安全问题不容忽视，科学合理地对能源需求进行预测对国家制定能源供应战略具有深远的意义。

针对能源需求预测问题，目前，常用的方法有能源消费弹性系数法、趋势外推法、灰色理论、时间序列等传统方法［1－3］。由于能源系统是一个高度复杂的非线性系统，各影响因素之间相互渗透，利用上述计量方法难以准确表达能源系统的内在结构和复杂特性，致使预测精度不高。

近年来一些学者将人工神经网络应用到能源需求预测中，人工神经网络作为一种并行的计算模型，有很强的非线性映射能力。对被建模对象的先验知识要求不多，一般不必事先知道有关被建模对象的结构、参数、动态特性等方面的知识，适应了能源系统的复杂性和非线性等特点，芦森建立了基于BP神经网络的能源需求预测模型对我国2010～2015年的能源需求量进行预测［4］，陶阳威等利用改进的BP神经网络对未来中国3年的能源需求量进行预测［5］，由于BP神经网络模型需要大量的样本数据才能得到较高的预测精度，当样本数据较少时，运用BP神经网络时得不到充分的训练，并还存在推广能力不强和过学习等缺点［6－7］，使得预测效果不理想。鉴于此，一些学者将组合模型应用到能源需求预测中，张婷运用灰色神经网络(GM－BP)组合模型对2010年和2020年中国的能源需求量进行了预测，结果表明该组合模型的预测精度优于GM模型和BP神经网络模型［8］，对于灰色预测，因其自身数据建模过程的局限性，采用灰色系统和BP神经网络的预测方法，在样本数据缺乏，即存在贫信息的条件下，这种组合的预测效果也是差强人意［9］。而广义回归神经网络（GRNN）在逼近能力、分类能力以及学习速度上较BP神经网络有更强的优势，网络最后收敛于样本量聚集较多的优化回归面，并且在样本数据较少时，预测的效果也较好。

本文通过对我国能源需求历史数据的分析，首先运用灰色模型提取历史数据信息，然后利用广义回归神经网络的高度非线性逼近能力，建立灰色广义回归神经网络（GM－GRNN）组合模型对我国能源需求量进行分析。

1 GM（1，1）和 GRNN 模型简介

1.1 GM（1，1）模型简介

灰色预测模型是将杂乱无章的原始数据经生成后，使其变成有规律的时间序列数据再建模，然后建立相应的微分方程模型，从而预测事物的未来发展趋势，在诸多的灰色模型中，以灰色系统中单序列一阶线性微分方程模型GM（1，1）模型最为常用。

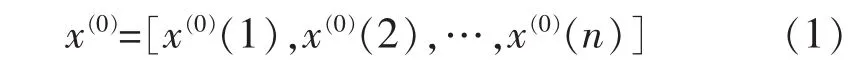
1） 设有原始数据序列 x（0），n 为数据个数。2）对原始数据序列累加以便弱化随机序列的波动性和随机性，得到新数据序列：

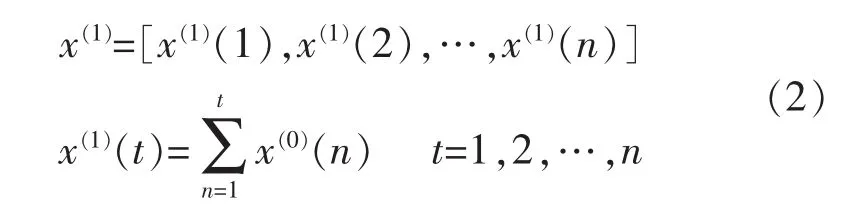
3）建立相应的微分方程模型为

式中：a、u是参数，分别称为发展系数和灰色作用量，只要求出参数 a、u，就能求出 x（1）（t），进而求出x（0）的未来预测值。

4）用累加生成数据构造累加矩阵B与常数项向量yn

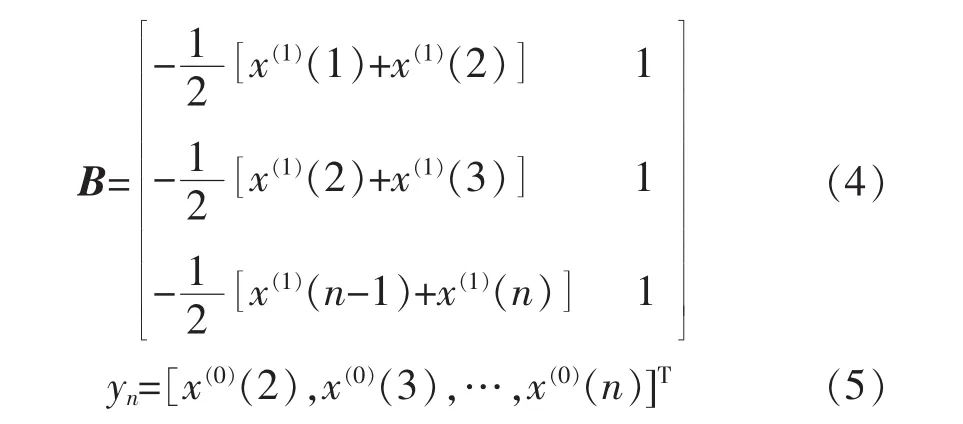
5）用最小二乘法求解灰参数

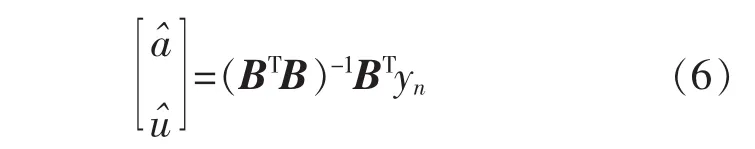
6）该微分方程的解为

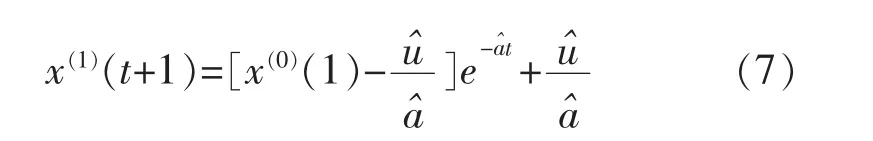
7）累减还原得到

1.2 GRNN神经网络的含义

GRNN最早由Donald F.Specht在1991年提出的［10］，建立在数理统计的基础上，它是径向基网络的变形，非常适用于对函数的逼近，其结构见图1。网络的第1层为径向基隐含层，神经元个数等于训练集样本数，该层权值函数为欧式距离函数（用||dist||表示），其作用为计算网络输入与第1层的权值IW1，1之间的距离，b1为隐含层的阈值，符号“⊗”表示||dist||的输出与阀值b1之间的关系，隐含层的传递函数为径向基函数，常用高斯函数作为网络的传递函数：

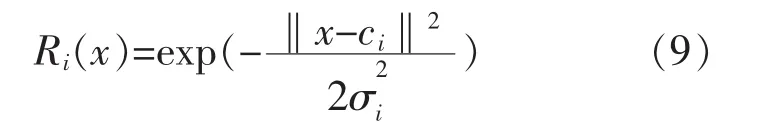
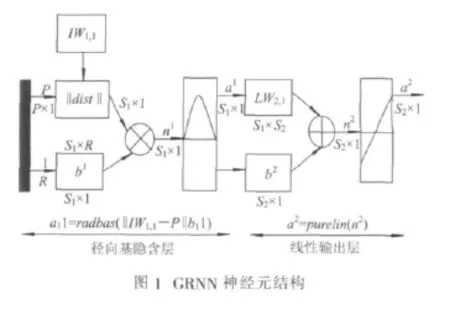
式中，σi决定了第i个隐含层位置中基函数的形状，σi越大，则基函数越光滑，所以称为光滑因子。隐含层节点的传递函数对输入信号在局部产生响应，当输入信号距离传递函数的中央较近时，隐含层节点产生较大的输出，故网络具有局部逼近能力。

网络的第2层为线性输出层，其权函数为规范化点积权函数，计算网络的向量n2，它的每个元素是由向量a1和权值矩阵IW2，1中每行元素的点积再除以向量a1的各元素之和得到的，将结果n2提供给线性传递函数

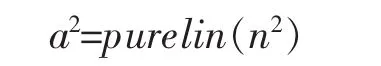
计算网络输出。

2 基于GM-GRNN的预测模型的构建

灰色预测模型适用于对近似指数增长、数据相对较少的数据序列进行预测，而且灰色预测方法的累加生成不但能削弱原始数据存在的随机性，而且使累加后的序列单调增长，突出了总体发展趋势［11］，适合用GRNN网络进行逼近。GRNN网络在样本数据较少的情况下，也可以达到一定的预测精度。因此将GRNN和GM预测方法结合起来，使它们互相取长补短，构造性能更好的能源需求预测组合模型是可行的。

根据以上分析，只保留灰色预测方法中的“累加生成”和“累减还原”运算，不再求参数a和u，利用GM－GRNN组合模型进行能源需求预测的算法如下：

1）确定影响因素 由于影响能源需求的影响因素众多，在不影响预测精度的情况下，对起关键作用的影响因素进行筛选；

2）灰色生成对原始数列进行灰色累加生成，得到累加序列：

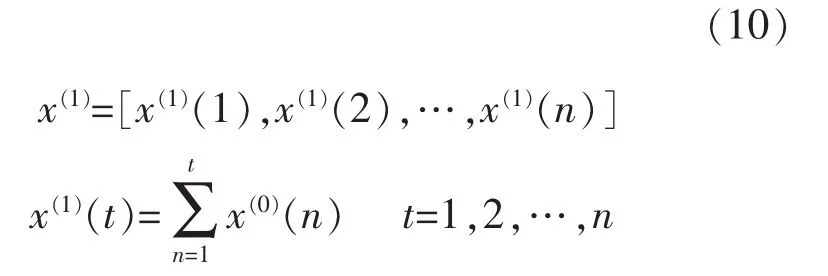
3）数据预处理 由于样本数据量纲存在较大差异，采用归一化方法中的线性函数转换的方法，将所有的输入、输出训练数据变换到［0，1］之间，归一化公式为

式中：xi，yi分别为转换前后的值；

4）GRNN网络训练与预测 利用GRNN网络对归一化后的数据进行训练和预测，输出累加序列的预测值；

5）白化处理 将累加数据的预测值进行进行“反归一化”和“累减还原”运算，得到能源需求的原始数据序列的预测值。

3 GM-GRNN能源预测模型实例分析

由于能源需求量的数据不易统计和查找，根据《中国统计年鉴》中相关的定义，能源消费总量指一定时期内，全国各行业和居民生活消费的各种能源的总和。该指标是观察能源消费水平、构成和增长速度的总量指标。本文在对能源需求进行分析时，以能源消费总量反映能源需求总量，构建GMGRNN模型对我国能源需求进行预测。

能源需求的产生受到很多因素的影响，并且这些因素对能源需求的影响程度不同，综合我国学者的研究成果［12－14］，合理选择影响能源需求的因素，影响能源需求的因素主要有经济、人口、产业结构、能源消费结构、技术进步、消费能力、城市化、能源价格、能源进出口、能源政策等因素，由于能源的种类不同，致使价格也不同，难以用统一的指标将价格量化，不考虑能源价格对能源需求的影响，对于能源进出口和能源政策，由于这2个因素都难以量化或者没有相关统计数据，也不考虑其对能源需求的影响。运用SPSS13.0软件对各影响因素在2000～2009年的相关历史数据进行相关分析，结果见表1，并选取影响能源需求的主要影响因素：中国人口总数、国内生产总值（GDP）、第二产业总产值、煤炭占能源消费中的比重、能源加工转化率、平均消费水平、城市化率。并作为网络的输入变量；以能源消费总量作为网络输出变量，样本数据见表2。

表1 各影响因素与能源消费总量的相关系数

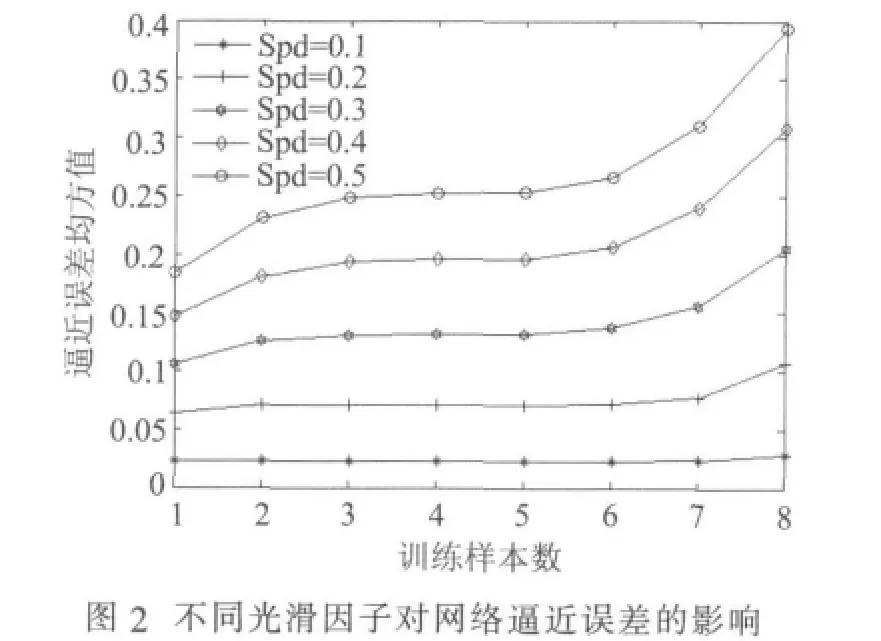
以我国2000～2007年共8年的历史数据作为网络的训练样本，选取2008～2009年共2年的历史数据作为网络的外推检验样本。对表1中样本数据进行灰色累加生成和归一化后，利用GRNN对处理后的数据进行训练，并需要不断调整光滑因子，本文将光滑因子分别设置为0.1，0.2，...0.5，对网络进行训练和仿真，得到网络对训练样本的逼近误差和对测试样本的预测误差分别见图2～3，由图2～3可见，光滑因子越小，网络对历史数据的逼近性能就越强；而光滑因子越大，网络对历史数据的逼近过程就越平滑，当光滑因子为0.1时，网络的逼近性能和外推预测性能的误差都较小，故选取光滑因子为0.1。

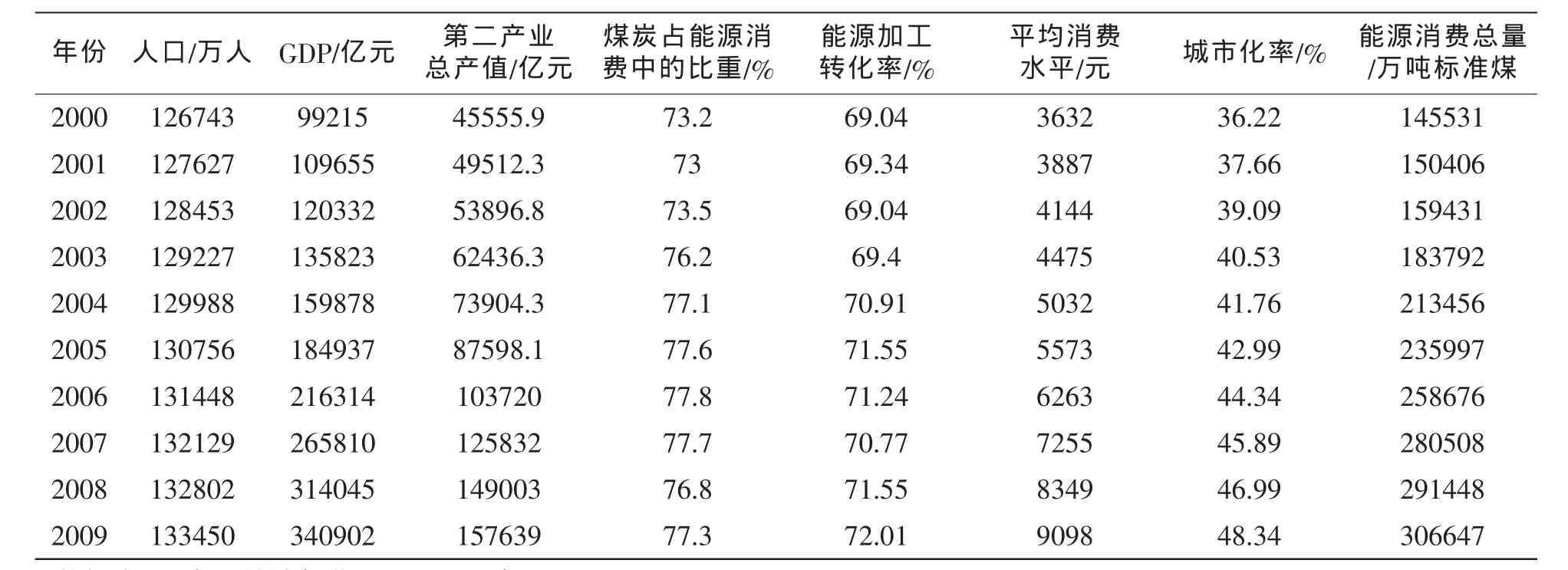
表2 样本数据

为进一步验证GM－GRNN组合模型的可行性和有效性，本文分别对 GM（1，1）模型、GRNN 模型和GM－GRNN组合模型的拟合和外推结果进行检验，其中GRNN模型和GM－GRNN模型均取光滑因子为0.1，结果见图4和表3。其中RMSE为样本均方标准误差；R为相关系数，反映预测模型对历史数据的拟合情况，R越大，预测模型的拟合效果越好；MAD为平均绝对误差；MAPE为平均绝对百分误差，它可以衡量不同预测模型的优劣，MAPE越小，预测模型的外推能力越强，即预测性能越好。

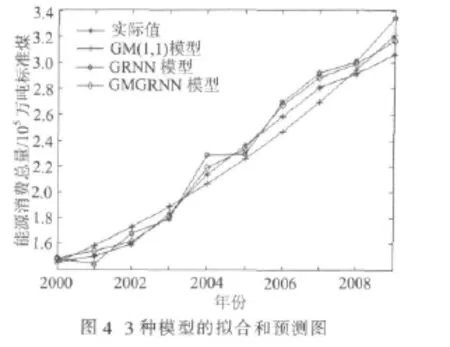
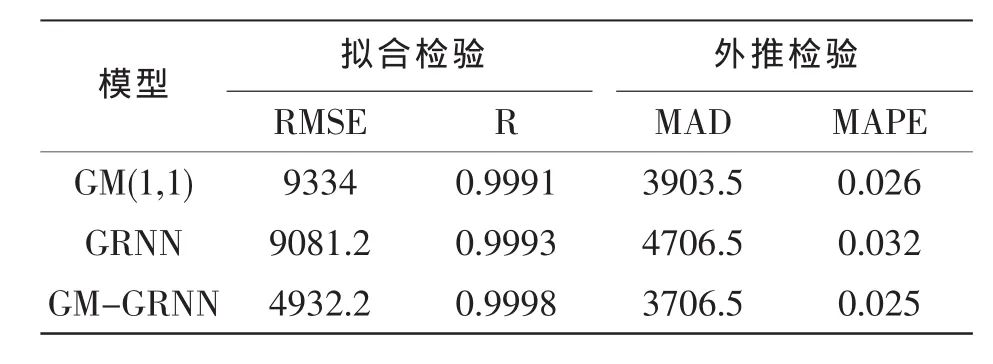
表3 3种预测模型的结果检验比较

从以上3个模型的检验结果可以看出，在样本数据较少的情况下，GM－GRNN组合模型较好地解决了小样本条件下的预测精度问题，与GM（1，1）模型、GRNN模型相比，在对历史数据的拟合和外推检验方面都具有更高的精度。

4 结论

针对灰色预测和广义回归神经网络的优缺点，将两者结合起来，建立GM－GRNN预测模型，既利用了灰色预测抗干扰能力强的优点，又发挥了GRNN非线性逼近能力强，需要样本数据少的优点，该组合模型的拟合和预测性能较好，并且模型建立过程简单，涉及参数少，适合对我国能源需求量进行预测。

由于我国能源系统具有高度复杂、非线性、小样本等特点，能源需求预测受诸多因素的制约，并非一种方法或模型能准确预测。对于GM－GRNN组合模型在应用过程中，可以对模型结构进一步优化，使模型的预测精度进一步提高。

［1］ 周倩，黄树红，李爱军.湖北省能源需求预测及分析［J］.统计观察，2007（4）：89－90.

［2］ 杜雨潇.基于ARIMA模型对我国能源需求的预测［J］.统计教育，2008，108（9）:60－61.

［3］李博，靳取.三种能源需求预测方法的比较分析－以四川省为例［J］.吉林工商学院学报，2009，25（1）:20－21.

［4］ 芦森.基于组合模型的中国能源需求预测［D］.成都:成都理工大学，2010:28－40.

［5］陶阳威.基于改进的BP神经网络的中国能源需求预测研究［J］.山西财经大学学报，2010，32（2）:47－49.

［6］ Moody J E.The effective number of parameters:Ananalysis ofgeneralization and regularization in nonlinear learning systems［J］.NIPS，1992，4:847－854.

［7］ Sa Zi M Y，Ceylan H.Use of artificial neural networks for transportenergy demand modeling ［J］EnergyPolicy，2006，34（17）:3165－3172.

［8］ 张婷.基于灰色神经网络组合模型的能源需求预测［D］.天津:天津大学管理学院， 2007:1－30.

［9］崔巍，刘洋.基于GM－GRNN预测模型的珠江水系集装箱运量分析 ［J］.珠江水运 （中山）发展大论坛，2011.18－19.

［10］ SPECHT D F.A general regression neural network［J］IEEE Transactions on Neural Networks 1991，2 （6）:568－576.

［11］ 关昌余，裴玉龙.基于GM－GRNN国家高速公路网规模预测研究［J］ .公路交通科技，2008 ，25（4） :142－145.

［12］孙涵，杨普容，成金华.基于MATLAB支持向量回归机的能源需求预测模型 ［J］.系统工程理论与实践，2011，31（10）:2002－2003.

［13］王珏，鲍勤.基于小波神经网络的中国能源需求预测模型［J］.系统科学与数学，2009，29（11）:1543－1545.

［14］ 武英涛，王克强.上海市能源需求预测研究［J］.上海经济研究，2011（1）:98－99.