地表水水量和水质的联合实时控制

1 前言

很多天然河流和渠道由于受到污染而出现水质问题。本文以圩田系统为例，图1是一个典型的荷兰圩田，属于被堤防环绕的低洼区域，区域内很多沟渠通过水利设施(如堰闸)彼此相连。其外围的运河海拔较高，可以储存雨季多余的水量，以在干旱期间给圩田提供淡水。通过水利设施，可使圩田沟渠和运河的水位维持在接近控制水位，并维持圩田内的固定地下水位，避免蓄水运河堤防决口。由于很多营养元素(如氮或磷)排放到沟渠内，使水质受到影响。夏季由于受到盐碱地渗漏和温室排水影响，地表水水质也会恶化。

在圩田水管理中，水量和水质为独立控制。为了控制水质，根据系统状况，按特定间隔时间使用既定的冲洗策略，3 d 1次。该策略是基于污染的最坏情况，即全年都可能发生污染。例如，在一场大雨过后，许多化肥养分迅速排入沟渠，导致水质恶化。因此，为应对干扰，应采用实时控制。水质传感器能连续按秒收集测量成果，甚至可以在浑浊的水环境下工作。

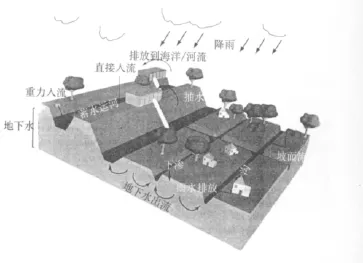
图1 荷兰圩田示意

在实例中，控制了几个运河河段(多变量控制)和制订了多目标(水位和水质控制)。MPC是一种先进的控制技术，可以对特定限制条件进行优化。在MPC用于水质时，需要用向前估计来预测各河段内的控制变量。这些预测成果是需输入MPC简化模型的部分信息。在MPC优化的外围，执行向前估计。图2为实施过程。本研究创新之处是以综合框架将水量和水质控制方法相结合。

2 方法

2.1 向前估计

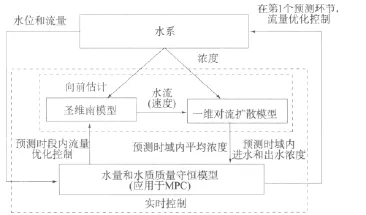
图2 向前估计及MPC水量和水质控制示意

向前估计为预模拟水流和污染物输移。采用圣维南方程和一维对流扩散输移方程两个线性近似解，来预测河段入流、出流和平均浓度。基于已优化的控制流量，预测涵盖整个范围。方程(1)～(3)说明向前估计中使用的这些偏微分方程。对于输移方程，假定横断面混合瞬时完成，在运河冲洗期间，假定污染物不发生降解。图3为运河河段示意。

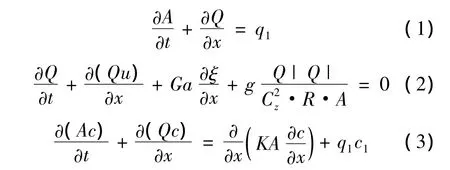
式中，A为过水断面面积，m2;Q为流量，m3/s;u为平均速度(m/s)，u=Q/A;ζ为基面以上水深，m;Cz为谢才系数，m1/2/s;G为重力加速度，m/s2;C为平均浓度，g/m3;C1为侧向水流的浓度，g/m3;t为时间;x为水平距离;q1为单位长度上的侧向流量，m3/s/m;R为水力半径(m)，R=A/Pf(Pf是湿周，m);K为离散系数，m2/s。

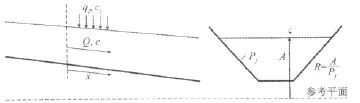
图3 运河河段示意

用菲舍尔提供的方程，计算纵向离散系数K:

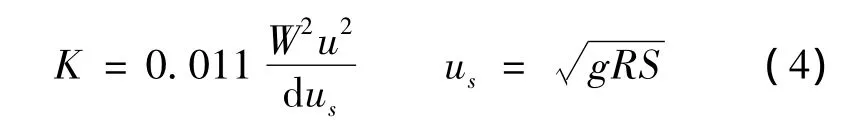
式中，W为平均河宽，m;D为平均水深，m;us为剪切流速，m/s;S为运河河底坡度(比降)。

结合一阶迎风近似值，以交错传统方案的形式开发了空间离散方程(1)～(3)。在交错网格上，缺少点i的*ui值和点(i+1/2)的*C值(图4)。应用迎风近似值，获得水流方向的数值。

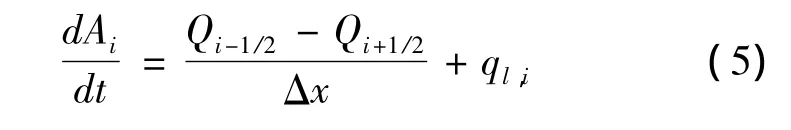
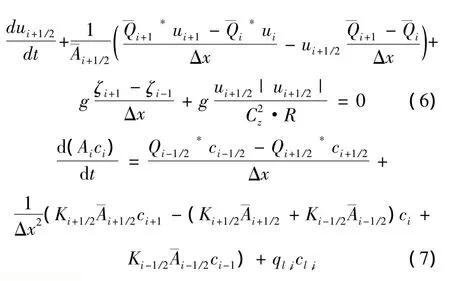
其中:

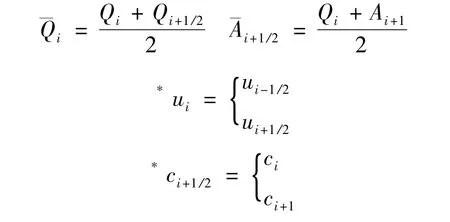
时间集成方案是根据“Theta”法。方程彼此连接，从而形成三阶矩阵方程。

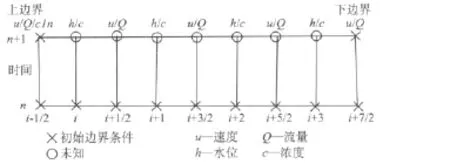
图4 交错一维网格示意

2.2 模型预测控制

自20世纪70年代以来，MPC在工程领域得到较好的运用，近年来被引进到水质管理，用于各种开放式运河及其支流的水位控制(见图5)。

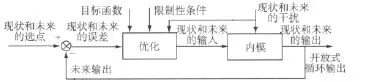
图5 MPC框架

MPC需要其他模型来预测系统的未来特征。常用圣维南方程和对流扩散输移方程来描述水深较浅水系的水量和水质动态。源于控制理论的一个离散的时间变体状态空间模型可以表示为:

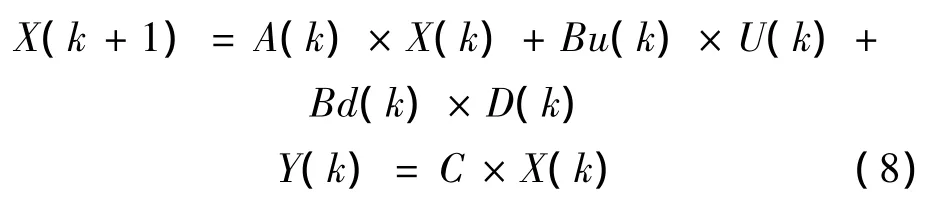
式中，X(R)为状态向量;D(k)为干扰向量;U(k)为输入向量;A(K)为状态矩阵;Bu(k)为控制输入矩阵;D(k)为干扰矩阵;C为输出矩阵;Y(k)为输出。该方程由矩阵构成，可用MATLAB范例求解。

圣维南方程制定了许多线性近似解，特别是灌溉水渠。将整个渠道分割成几小段，用正式的估计器或观测器来估算每段液压信息。然而，这种近似解不适合MPC，只有简化模型来保证系统的主要特性。因此开发了积分滞时模型，即集总参数模型。假设整个渠道的两个元素分别为均匀流部分的延时特征和回水部分的水面面积特征，则:

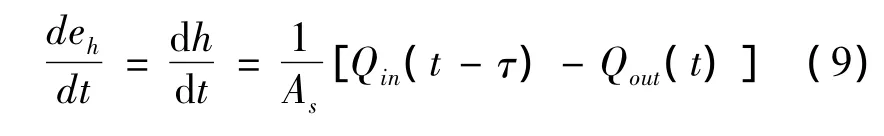
式中，eh为与控制水位的水位偏差，m。当控制水位为常数时，该值与水位h有同样的导数;Qin为入流流量，m3/s;Qout为出流流量，m3/s;As为回水水面面积，m2;τ为均匀流部分的延迟时间，s。

为简化水质模型，有人提出了一个湖泊模型，该模型作为完全混合系统维持质量守恒。如果湖泊的平均浓度和出流浓度可以计算出来，该模型可以修正成一个非混合系统。在该条件下，可用向前估计模块计算。则水质质量守衡方程为:

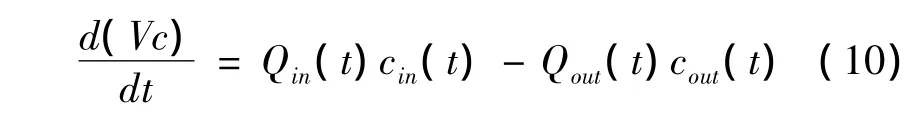
代入水体质量守衡方程，方程(10)变为:

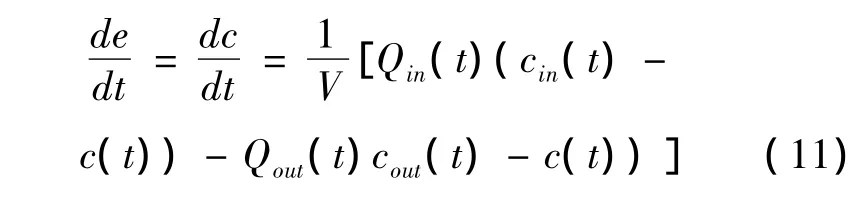
式中，V为河段槽蓄水量，m3;ec为平均浓度与控制浓度的偏差，g/m3，当控制浓度是常数时，该值与平均浓度c有相同的偏差;cin、cout为入流和出流浓度，g/m3。

对于MPC，目标函数用来描述水量与水质相结合的控制目标:

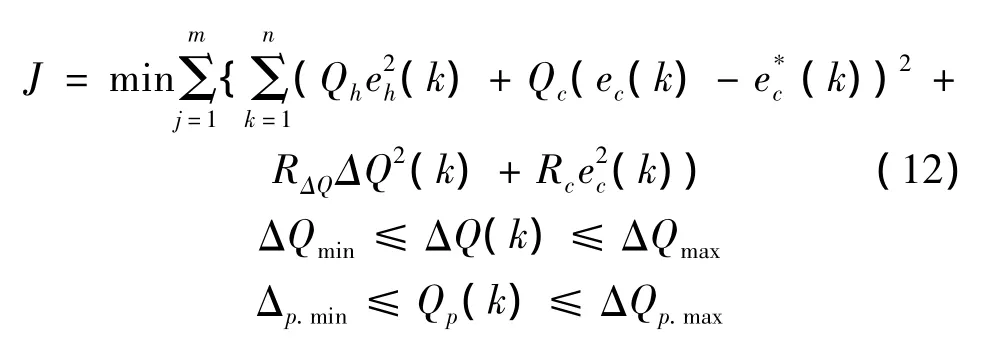
式中，N为预测时段内的总步骤数;M为运河总河段数;ΔQ为变化流量(包括闸门和抽水泵)，m3/s;Qh，Qc和 R ΔQ 为 eh、ec及 ΔQ 各自的损失;ec为模拟变量，作为软限制条件，g/m3。

软限制条件是指当河段水体清洁时(低于控制浓度)可不进行水质控制，即当河段现状或输入违反限值时，作为附加损失，可执行软限制条件。RC是模拟输入损失，其值非常小，这使无论ec(k)取多大值，Rcec2(k)几乎都等于零。QP代表泵抽水流量，m3/s;ΔQ和Qp是绝对不能违反的硬限制条件。

3 测试案例

3.1 案例设置

3个水上闸门将运河分隔成4小段。表1为各段水量和水质控制目标。图6为运河特征。为使空间离散，每个河段又被分成100个长10 m的小段。在出现控制盐分情况时，设想污染物至少在冲洗期间低于实际数量。在每个时间步长，通过方程(4)估计每个离散速度点的离散系数。通过1号闸门从蓄水运河引入淡水，使用抽水泵使另一端的水体离开系统。每个河段有几个已受到污染的侧向流，且对系统形成干扰。表2为其初始流量和浓度。

表1 水位和浓度控制值

表2 每个河段的侧向流量

表3 MPC目标函数损失

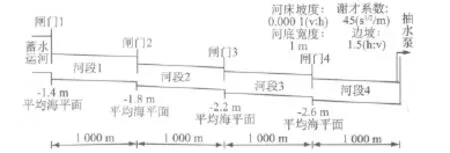
图6 运河纵剖面的几何特征

总模拟时间为20 h。在模拟过程中，第2个河段的侧向水流浓度在5 h内由1.4 g/m增至5.6 g/m(1步变化)，之后保持不变。其他侧向浓度和流量依然存在。侧向浓度的增加为随机性，假定所使用的精确干扰方案与实时控制评价无关。案例说明实时控制如何纠正水质干扰，同时又能维持水量标准。整个系统在MATLABS进行模拟和测试。

3.2 MPC设置

内置模型和目标函数与预测控制模型部分一致。在状态空间模型中，X(k)包括选点的水位偏差、浓度偏差和延时步长下的流量;U(k)包括每座建筑物的流量变化和每个河段的实际输入ec(k)，这些条件决定着是否进行水质控制;D(k)包括所有侧向流。离散延迟步长通过水流输送时间(L/估计，其中:L为运河长度，m;R为水力半径，m;g为重力加速度，m/s2;u为平均流速，m/s。计算导致每个河段有2个延迟步长再加上4 in控制时间。MPC控制器使用1 r测时段。当MPC检测到时段内侧向浓度有变化，必须调整当前控制步骤的流量。

要想获取设置目标函数起点损失的方法，只有反复试验，不断调整参数。见表3。

3.3 传统控制设置

PI是常用的水管理控制方法。对于干扰，它相对简单和强劲，已在灌溉和河道水位控制系统中得以应用。在此使用PI，是为了同MPC的性能进行比较，以说明后者的优势。PI控制原理可表达为:

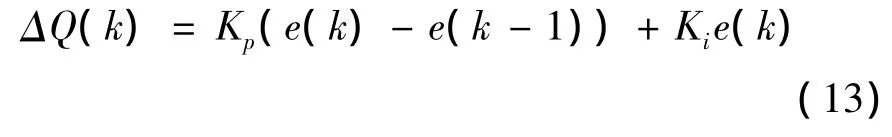
式中，K为离散时间指标;ΔQ为某一设施的流量变化，m3/s;Kp、Ki为比例和积分增益因子;e为控制水位的水位偏差，m。

通过确定e，可将该方法扩展运用于水质控制。在圩田冲洗情况下，1号闸门(流入到系统)与污染最严重河段的水质变量相连接，其余闸门和抽水泵借助于分离器，对每一个河段的水位在当地上游实施控制。该分离器为反馈控制，具有弱化上下游河段之间水流相互影响的功能。在这种情况下，分离器直接向其他所有设施发送上游闸门的水流信息，从而避免水位的异常波动。

表4显示了PI控制选定的增益因子。

表4 PI控制增益因子

4 结果

图7～11为PI和MPC的模拟结果，显示了闸门和抽水泵流量与控制值的水位偏差和平均污染物浓度偏差。图7～9是PI控制结果，图10～11是MPC的结果。显然，随着水质步长变化，PI和MPC都能稳定水位和恢复水质，使其回到控制值。都可将系统从一种状态移到另一种状态。

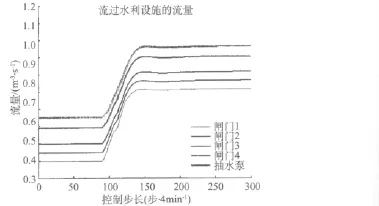
图7 水利设施排水量(PI控制)

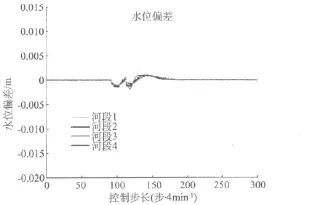
图8 水位偏差(PI控制)

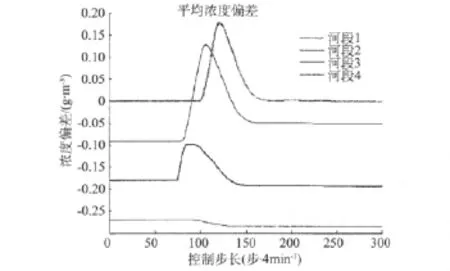
图9 平均浓度偏差(PI控制)

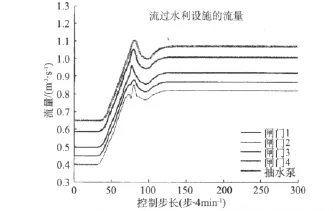
图10 水利设施排水量(MPC)

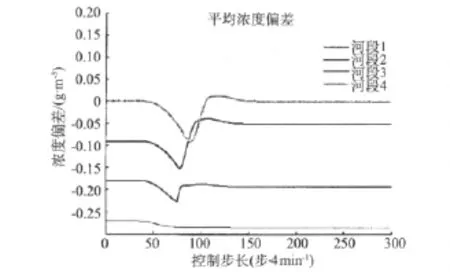
图11 平均浓度偏差(MPC)

运用PI控制，当步长发生变化时，闸门1号会响应，这代表水质恶化时刻出现。同时，水位控制器会降低每个水池末端的水位。图8～9显示PI能有效维持水位，但河段3和4的水质恶化比较严重。

MPC可根据预测情况提前调整系统(每4 h预报一次)。当检测到时段内侧向浓度增加时，MPC向系统排放干净水流，以在第一时间降低水体浓度。通过对比PI控制结果(图7)，可以看出，当侧向变化实际发生时，浓度增加有更大的空间。PI控制的浓度峰值要高很多，表明与MPC有显著差异。图9和图11也反应出这种差异特性。图12显示MPC可将水位控制在一个相对安全的范围内。

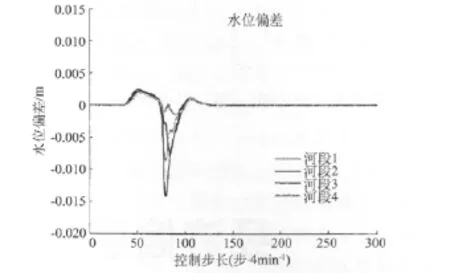
图12 水位偏差(MPC)

5 结论与讨论

以圩田潮红为例，探讨了地表水水量和水质联合控制的创新方法，并对其应用成果作了总结。

(1)PI和MPC都能维持水位，并在渠道洗井期间，恢复其水质至目标值。

(2)PI控制是采取后期行动，而MPC的优势是预测，寻求浓度偏差小，冲洗策略最佳。

(3)当向前估计程序应用于简化的MPC水量和水质模型时，其可行性得到了证实。

根据对MPC和PI应用结果的比较，需对以下3个方面开展讨论。

(1)功能。PI比MPC的操作简单，所需计算时间较少。PI控制可以使系统相对稳定，但其功能有限(第1号闸门控制水质，其余维持水位)。PI控制专为运河冲洗而设计。用于系统内水量少，水质较好的情况，但不能向下游供水，因为第1号闸门的调度不是用来维持水量。而MPC是一个统筹考虑了水量和水质的多目标控制系统，因此它比PI的控制功能更多。

(2)灵活性。MPC考虑到了系统在优化方面的局限性。在严重浓度峰值到来前，它可基于预测提前做出响应，创造附加机动时间。特别是当水质偏差幅度很小，限制性条件很容易被违反时，该机动时间非常重要。而对PI而言，违反限制性条件可能无法避免，或仅通过非常严格的控制来缓和。

(3)执行困难。仅使用现场测量结果无法满足MPC的要求，它需运用适当的模型预测未来的行为。而PI只在发生偏差时做出响应，测量结果足以满足控制器所需。这使PI控制更加容易实现。