基于ANFIS替代模型的水库水质调度规则开发

［伊朗］F.苏丹尼

1 概述

20世纪70年代初期以来，耦合模拟优化模型已被广泛应用于水质管理，但是水库调度研究中重点考虑水质问题的很少。有专家开发了下游水质控制的最优水库调度策略，以及运用动态规划辨识水库最优浊度控制调度策略。后来又有学者开发了一种水库调度优化模型，该模型可使系统总成本降到最低，包括盐害的损失费用。

1996年，针对用于水力发电和下游河流水质控制的两水库系统，提出了一种多目标公式。1998年，耦合了水质模拟模型和最优控制算法，通过在一个河流－水库系统中修改调度操作，以评价水质改善的可能性。在受流量和上游水位各种调度约束，以及保持水质目标的条件下，力图使水力发电效益最大化。

2006年，有学者耦合神经网络和遗传算法，对台湾翡翠水库的水质管理开展研究。首先，用人工神经网络(ANN)模型模拟水库入库营养物负荷的性状，并用流域负荷、降水量、出流量数据预测水库总磷浓度。

为解决水库和河流－水库系统中的水质管理问题提出过两种随机模型。为减少基于遗传的优化模型运行时间，已运用序贯博弈理论概念来开发一种遗传算法(GA)，称为变长染色体遗传算法(VLGA)。但是这些模型运行时间相当长。

2008年，为水库水质管理提出了一种新型冲突消解模型，利用冲突消解理论来解决决策者和利益相关者的现有利益冲突。2010年，开发出了一个基于遗传算法的水库调度优化模型，并考虑了与水量和水质有关的目标。然而，却不能为水库泄水孔的调度规则提供任何方法。

为缩短上述优化模型的运行时间，用一些经过训练的ANFIS替代水质模拟模型。为进一步缩短其运行时间，将主要问题分解为一个长期优化模型和几个年优化模型。运用该优化模型提供的最优调度策略来训练其他ANFIS模型，以开发水库月调度规则。

2 模型框架

为对本文提出的模型与其他模型进行比较，本文考虑了一个类似的目标函数。

最大化:

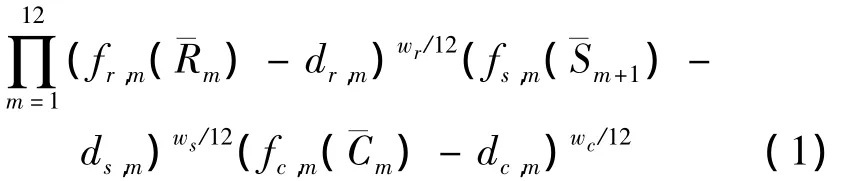
式中，fr，m()/dr，m分别表示与m月需水量下分配水量有关的效用函数和分歧点的值;fs，m()/ds，m分别表示与m月月底蓄水量有关的效用函数与分歧点的值;fc，m()/dc，m分别表示与m月期间配给水中选定的水质指标浓度有关的效用函数与分歧点的值;表示m月水库平均下泄量，106m3;wr，ws，wc分别表示负责供水、蓄水和分配水水质的决策者/利益相关者的相对职权值(权势或重要性权值)表示m月初水库平均蓄水量，106m3;表示m月水库下泄水体水质指标平均浓度，mg/L。

考虑典型约束，如与水库水连续性、水库库容和下泄能力有关的约束，应将该目标函数最大化。y年m月泄水孔k的出流水质Ck，m，y，可通过以下典型方程获得:

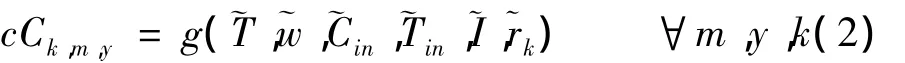
式中，g()表示水库水质模拟模型提出的函数表示气温时间序列，℃;表示入流水温时间序列，℃表示气候变量的时间序列，如短波辐射、露点等;~T表示入流时间序列，106m3~表示泄水孔k的下泄量时间序列，106m3;表示水库入流中水质指标浓度的时间序列，mg/L。

采用训练有素，且模拟时间短的ANFIS来评估Ck，m，y。为进一步减少模型运行时间，将主要问题分解为一个长期优化模型和若干个年优化模型。考虑到纳什乘积函数(公式(1))，长期和短期优化模型的目标函数分别为

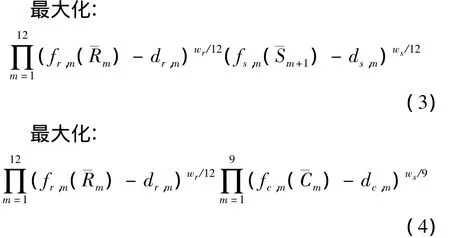
长期模型的目标函数与供水可靠性有关。通过长期模型获取的调度规则提供每个水年年初和年末最优水库蓄水量时间序列。这些水库最优蓄水量值被看作年水库调度优化模型中的约束条件。年模型的目标函数与分配水的水质水量相关。为减少库中积聚的污染物，考虑1 a有3个月用来冲洗水库和释放污水。这3个月中，不考虑目标函数中的水库下泄水水质(参考公式(4))。流程见图1。

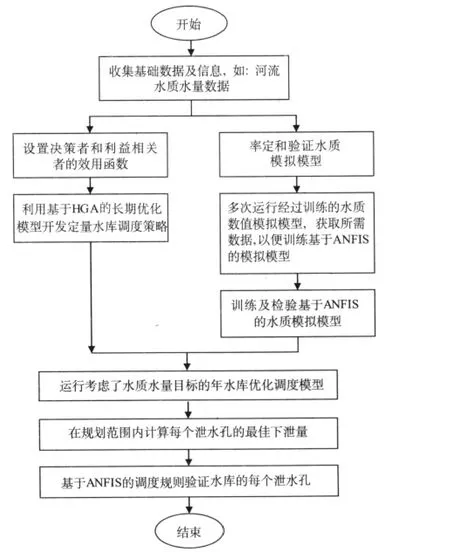
图1 考虑水量水质目标的水库调度流程

3 水质数值模拟模型

目前已知的水质模拟模型如 HEC－5Q和WASP7，已广泛应用于水库水质模拟，但它们不易与这些优化模型耦合。为此，开发了一维水质模拟模型。该模型考虑HEC－5Q的主要假设条件，并对每种水质成分求解平流－护送散质量传输方程。在研究中，深水库用一系列水平层表示，且每一层的特征点用表面面积、厚度、体积表示。每一层中假设水体完全混合，且垂直梯度不变。

运用该数值模型的几种运行结果来训练和测试基于ANFIS的模拟模型。将经过训练的ANFIS与优化模型耦合。

4 自适应神经模糊推理系统

1993年首次提出自适应神经模糊推理系统(ANFIS)，它是一种通用的逼近器，相比传统统计方法，能更有力地描述高度非线性函数。从功能上来说，ANFIS相当于一系列规则组成的模糊干扰系统，可以根据模糊的“如果－那么”型，基于规则和规定的输入输出数据，对构建输入输出映射。它运用神经网络训练程序，来调整隶属函数和相关参数。为介绍ANFIS结构，考虑了基于一阶Sugeno模型的两个模糊的“如果－那么”型假设规则。

(1)如果x为A1，y为B1，那么

(2)如果x为A2，y为B2，那么

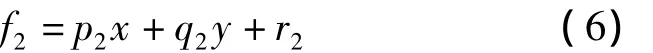
式中，x和y为输入变量;Ai和Bi为模糊集;fi为该模糊规则模糊区域内规定的输出变量;pi、qi和ri为设计参数，在训练期间加以确定。通常ANFIS模型有5层，构形类似于任何一个多层前馈神经网络，见图2。作为一个5层前馈神经结构，ANFIS中的节点功能，可概括如下。

(1)第1层。节点是自适应的，将输入变量的隶属度函数作为节点函数

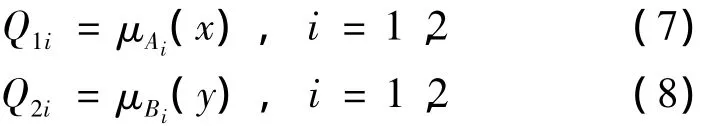
式中，μAi(x)和μBi(y)可采用任何模糊隶属函数。参数的去模糊器。

(5)第5层。单节点是固定的，其输出等于所有输出之和。

学习适用于这种结构算法，旨在调整所有可更改的参数，即{ai，bi，ci}和{pi，qi，ri}，使 ANFIS 的输出匹配训练数据。通常采用一种结合最小二乘法和梯度下降法的混合算法解决这类训练问题。前提参数{ai，bi，ci}选定之后，用最小二乘方法优化后件参数{pi，qi，ri};运用前一步得出的后件参数计算ANFIS的输出结果。通过标准误差反向传播算法，用输出误差修改前提参数。

文中，训练两个ANFIS模型来模拟水库水质和开发水库月调度规则。利用水库水质数值模拟模型结果对第1个ANFIS进行训练;利用从水库调度优化模型中获得的最优调度策略训练第2个。

5 混合遗传算法

例如，如果采用了钟形隶属函数，则μAi(x)可表示为

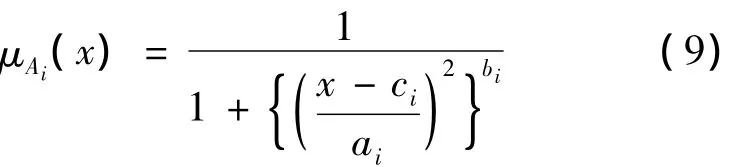
式中，ai、bi、ci为隶属函数的参数，可相应地调节钟形函数。

(2)第2层。节点是固定的，并用M标注，表明其作用如同一个简单地乘数。其输出可表示为

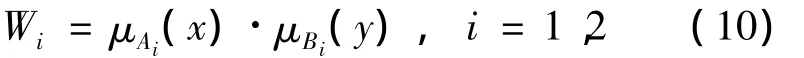
(3)第3层。节点是固定的，用N标注，起标准化的作用

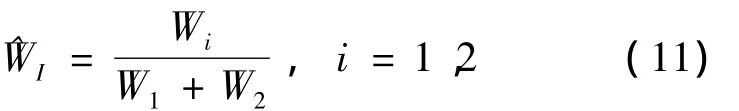
(4)第4层。节点是自适应的，其节点函数由第1层给出，以运用于一阶模型，其参数被称为后件

运用混合遗传算法求解提出的优化模型。遗传算法是基于自然选择过程，既可解决约束问题也可解决无约束问题的方法。该过程可促使生物进化。遗传算法反复修改一组个体解，每一步都会从总体中随机选择个体作为交代，产生下一代。经过接连几代，种群朝最优化“进化”。可用遗传算法解决各种不适宜标准优化算法的优化问题，包括目标函数不连续、不可微、随机性或高度非线性。

混合遗传算法中，在遗传算法运算终止后开始运行一种模式搜索算法，以便改善适应度函数值。混合函数将遗传算法获得的最后点当做其初始点。模型搜索算法可估算一系列越来越靠近最优点的点。每一步中，该算法在当前点的附近搜索一组点，叫做网格。如果模式搜索算法发现网格中的某一点提高了当前点的目标函数值，则在下一步中新点变成当前点。

6 个案研究

为评估提出的模拟优化模型的有效性，将其应用于伊朗中部的第15科尔达德(15－Khordad)坝。该坝1994年建于代利詹(Delijan)市附近的哥姆卢德(Ghomrud)河上，有效库容2亿 m3，年均入流1.77亿m3，主要为位于该坝下游的一个大型工业综合体以及8 000 hm2农田供水，农田年需水量1亿m3。坝的主要特征示于表1。从表1可知，水库有两个泄水孔、一条自由泄水的溢洪道。

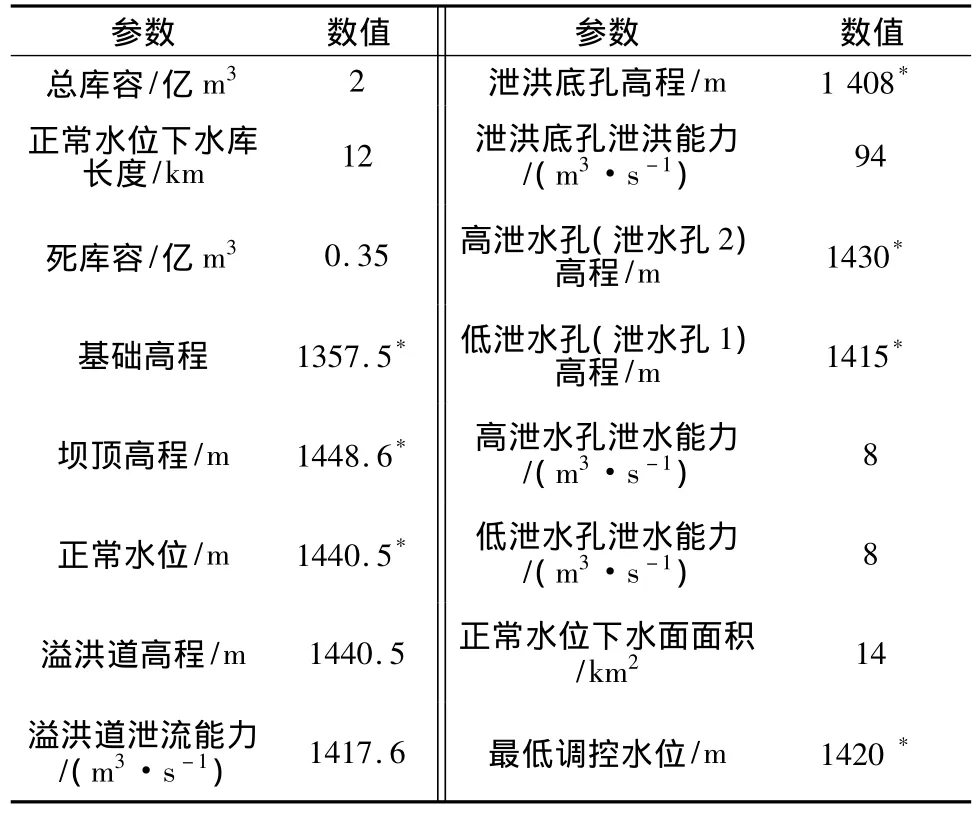
表1 第15科尔达德坝的主要特征

水库水体盐度往往不符合水质标准。因此，总溶解的固体颗粒(TDS)和温度被认为是水质指标。伊朗水研究中心在1997～1998年对水库水质进行了监测，在沿水库长度13个横截面观测了几个水质变量，如:温度、TDS和溶解氧(DO)。在每个横截面中均采集水库几个不同深度的样本。由于忽略了水质变量浓度的水平变化，因此可用一维水质模拟模型来模拟水库水质。

公式(12)由用水户确定，表明该部门的效用是针对每月需水量的配给水量的函数。公式(13)表明水库调度者的效用函数与水库月蓄水量有关。考虑到溢洪有很高的泄水能力及下游年需水量，当蓄水量大于1.3亿m3时，决策者效用函数值为1;当蓄水量在0.35亿～1.3亿m3时，效用函数值小于1。

公式(14)和(15)由卫生部和环境保护署确定。当分配水水量很重要时，公式(14)迫使模型在3～11月提供低盐度下泄量。当需水量很少时，可根据公式(15)将水库12～次年2月的下泄量用来冲刷水库和控制累计盐度。

7 结果和讨论

对第1个ANFIS模型，利用数值水质模拟模型几组运行结果进行训练和检验。在不同月份对不同ANFIS模型进行水质模拟训练。其月输入量如下:

(1)月水库入流量;

(2)月初水库蓄水量;

(3)水库低泄水孔的下泄水量;

(4)水库高泄水孔的下泄水量;

(5)月初水库蓄水量中上层水体的TDS浓度;

(6)月初水库蓄水量中中层水体的TDS浓度;

(7)月初水库蓄水量中底层水体的TDS浓度。

由于每个ANFIS有一个输出量，所以建立了4个ANFIS模型进行每个水库水质模拟。这4个模型提供每月水库出流中TDS平均浓度以及月末水库蓄水量的上、中和底层水体的TDS浓度。为了进行水库水质模拟，在规划期限内要训练及检验48个ANFIS模型。在ANFIS模型中，对每个模糊输入量均考虑了3个高斯形模糊隶属函数。在训练过程中设定隶属函数参数。

图3～4显示了基于ANSIS的模拟模型之一的检验和训练结果，这些模型用于评估每月水库出流量中的TDS平均浓度。由图可知，经过训练的ANFIS模型在优化模型中可准确地模拟水库水质。

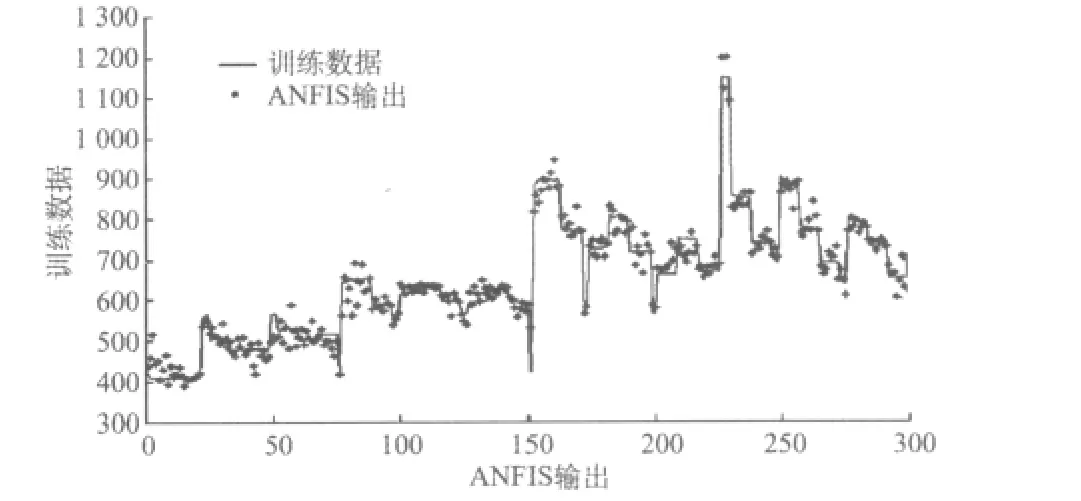
图3 基于ANFIS的模拟模型训练结果(评估6月份水库出流的TDS平均浓度(mg/L))

耦合基于经过训练和检验的ANFIS模拟模型和提出的优化模型，以获取水库泄水孔最优月出流量。水库泄水水质、需水量下的供水以及水库蓄水量三者的相对权重 wc，wr和 ws分别为 0.65、0.25 和 0.1。

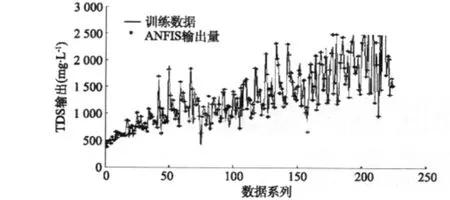
图4 基于ANFIS的模拟模型检验结果(评估6月份水库出流的TDS平均浓度(mg/L))

如图4所示，模型结果基本相同，但本文提出的模型可减少先前开发的两个模型的运行时间。训练的ANFIS有效，训练过程中只用了80%的现有资料。图5对运用基于ANFIS的调度规则获得的平均下泄盐度与先前提出的模型获得结果进行了比较。结果表明:基于ANFIS的调度规则可有效地应用于考虑水质问题的实时水库调度。

8 总结和结论

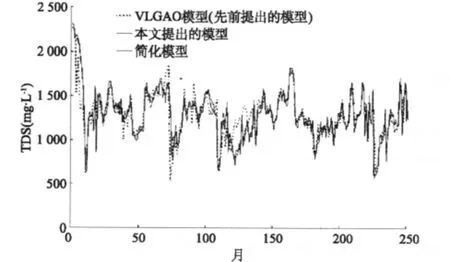
图5 本文提出的模型与VLGAO模型结果的比较

提出的基于ANFIS的优化模型仅可用于制定水库调度策略(不是调度规则)，水库调度策略是表示调度期间水库最优下泄量的时间序列。因为最优调度策略不能直接运用于实时水库调度，但可用于训练基于ANFIS的每个泄水孔的调度规则。入流水量水质、月份数以及月初水温和TDS浓度的垂直公布，被认为是每个基于ANFIS的调度规则的输入量。为使受

为减少VLGAQ模型和简化模型的运行时间，研发了一种耦合水质模拟模型和混合遗传算法的新方法，可用来确定水库不同泄水孔的最优调度策略。用一个校准的数值水质模拟模型的结果训练和检测一些ANFIS模型，并基于这些ANFIS模型构建水质模拟模型。

为进一步减少模型运行时间，将主要问题分解为一个长期优化模型和若干个年优化模型。运用优化模型提供的最优调度规则训练一些基于ANFIS的模拟模型，来研发实时水库月调度规则。

将该模型应用于伊朗中部的第15科尔达德水库。结果表明，运用新模型研发水库调度规则，尽管其与先前开发模型的最优调度策略几乎相同，但对减少计算负担具有重要价值。该程序易应用于长期规划或多水库问题。然而，随着水质指标数量的增加，新提出方法的总运行时间明显增加。