简单迭代法的敛散性讨论

张希娜，张 霞

(兰州理工大学技术工程学院理学部，甘肃 兰州 730050)

简单迭代法的敛散性讨论

张希娜，张 霞

(兰州理工大学技术工程学院理学部，甘肃 兰州 730050)

通过分析判断简单迭代法的收敛条件ρ(B)(迭代矩阵B的谱半径)的不同情况，比较完整系统地给出了简单迭代法敛散性的各种情况。

简单迭代法；敛散性

设方程组AX=b，则简单迭代法(Jacobi迭代)的迭代格式为:

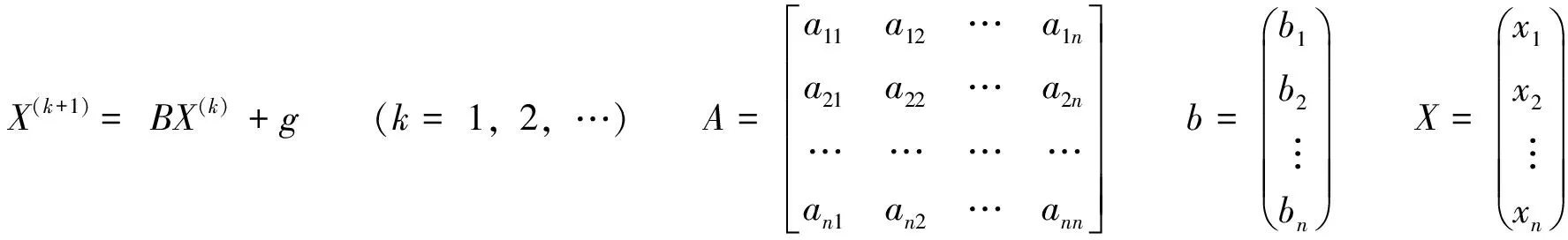
(1)

1 主要结果

命题1若ρ(B)<1，则对于任何初始向量X(0)和常数项g，由迭代格式(1)产生的向量序列{X(k)}收敛且极限与初值无关。

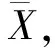
有εk+1=Bεk，k=1,2,…。即：

εk+1=Bεk=B2εk+1=…=Bk+1ε0

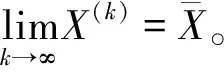
由命题1可以看出，迭代是否收敛只与迭代矩阵的谱半径有关，而迭代矩阵B是由系数矩阵A演变过来的，所以迭代是否收敛只与系数矩阵A以及变换的方式有关，而与初始迭代向量的选择无关。

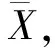
(2)

式(1)与式(2)相减，并反复递推，有：

(3)

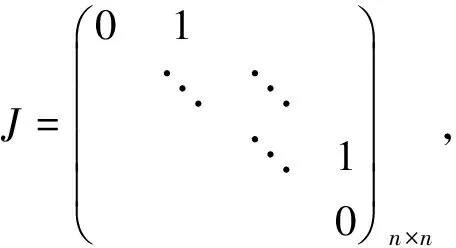
又在复数域上任何矩阵B相似于它的若当标准形，即有可逆阵P，使得P-1BP=J，其中：

式中，ni是B的特征值λi的重数，并且有(n1+n2+…+nr=n),i=1,2,…,r。从而：

代入式(3)有：

(4)

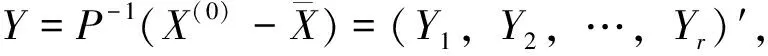
不妨设Y1=(y1,…,yn1)′≠0，将其代入式(4)中得:

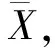
(5)

其中：

所以：

(6)

又因Y1≠0,即y1,y2,…,yn1不全为零，如果yn1≠0，则：

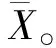
(7)

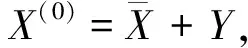
命题4若ρ(B)=0，则对任意初始向量X(0)，X(n)一定是方程X=BX+g的解向量，其中n是矩阵B的阶数。

(8)

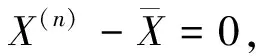
由于迭代格式(1)收敛的快慢与迭代矩阵B的谱半径ρ(B)的大小有关，ρ(B)越小，收敛越快，当ρ(B)最小为零时，此时收敛最快，由命题4知当迭代n步时就可以得到精确解。

2 结 语

通过对简单迭代法迭代矩阵的谱半径的讨论可以看到，对于任一方程组的敛散性都可以通过计算ρ(B)并加以判断而得到，也就是说计算ρ(B)是一种通用的方法，而对于一些特殊的矩阵，有一些特殊的判别方法，如对称正定、严格对角占优等等［1］。

［1］徐萃薇，孙绳武.计算方法引论［M］.北京：高等教育出版社,2003.

10.3969/j.issn.1673-1409(N).2012.07.004

O24

A

1673-1409(2012)07-N008-02

2012-04-13

张希娜(1983-)，女，2005年大学毕业，硕士，助教，现主要从事马尔可夫骨架过程及其应用方面教学与研究工作。

［编辑］ 洪云飞