交通网络的运输堵塞成本分析
葛长飞
(盐城师范学院商学院,江苏 盐城 224051)
交通网络的运输堵塞成本分析
葛长飞
(盐城师范学院商学院,江苏 盐城 224051)
交通网络堵塞对运输成本具有重大影响。提出了一个度量交通网络堵塞对运输成本影响的指标———运输堵塞成本。首先分别给出任意起止点对之间、一条路径及整个交通网络的运输堵塞成本定义,然后分析运输堵塞成本的性质和算法,最后用南通市实际局部交通网络进行实例分析,为相关部门进行交通运输规划提供依据。
交通网络;运输堵塞成本;算法
城市交通网络由城市范围内的所有道路构成,是城市的基本骨架,是城市社会经济活动的运输载体。城市交通网络性能的好坏直接关系到运输载体的效率。为了更好的衡量城市道路交通网络的性能,需要建立评价指标(如道路网密度、非直线系数、连接度、平均车速、饱和度等)。现实生活中,自然灾害、交通事故等会造成某些路段发生堵塞,这种堵塞在短时间内一般不能恢复,导致路网中点对的位置、最短路径长度和点对之间单位运输成本、某段时间内点对之间运输量不断发生变化[1]。为此,许多学者进行了相关研究[2-5],但上述研究缺乏对城市交通路网空间布局、成本和堵塞相结合的探讨。下面,笔者从道路交通规划部门的实际需求出发,对交通网络的运输堵塞成本进行了分析和研究。
1 运输堵塞成本指标的定义

定义1交通网络上任意起止点对的运输堵塞成本指标为:

定义1给出了交通网络中任意起止点对的运输堵塞成本指标,即交通网络任意点对最短路径上出现堵塞且堵塞不可恢复的情况下,比没有发生堵塞的情况下车辆多付出的成本。
定义2一条路径上的运输堵塞成本指标为:
定义2中给出了一条路径上的运输堵塞成本指标,即该路径上所有的点对的最短路径上都可能发生堵塞且堵塞不可恢复的情况下,比没有发生堵塞的情况下车辆多付出的成本之和。
定义3整个交通网络上运输堵塞成本指标为:
定义3给出了该交通网络中的运输堵塞成本指标,即交通网络中所有的点对和路径都可能发生堵塞且堵塞不可恢复的情况下,比没有发生堵塞的情况下车辆多付出成本之和。
2 运输堵塞成本指标的性质
G(V,E)上任意起止点对为(vi,vj)和(vi,vj+1),a为点对(vj,vj+1)的最短路径长度,b为(vj,vj+1)最短路径出现堵塞后且堵塞不可能恢复时替代路经长度。假设Cij=Cij+1,Dij和Dij+1服从某种随机分布,则:
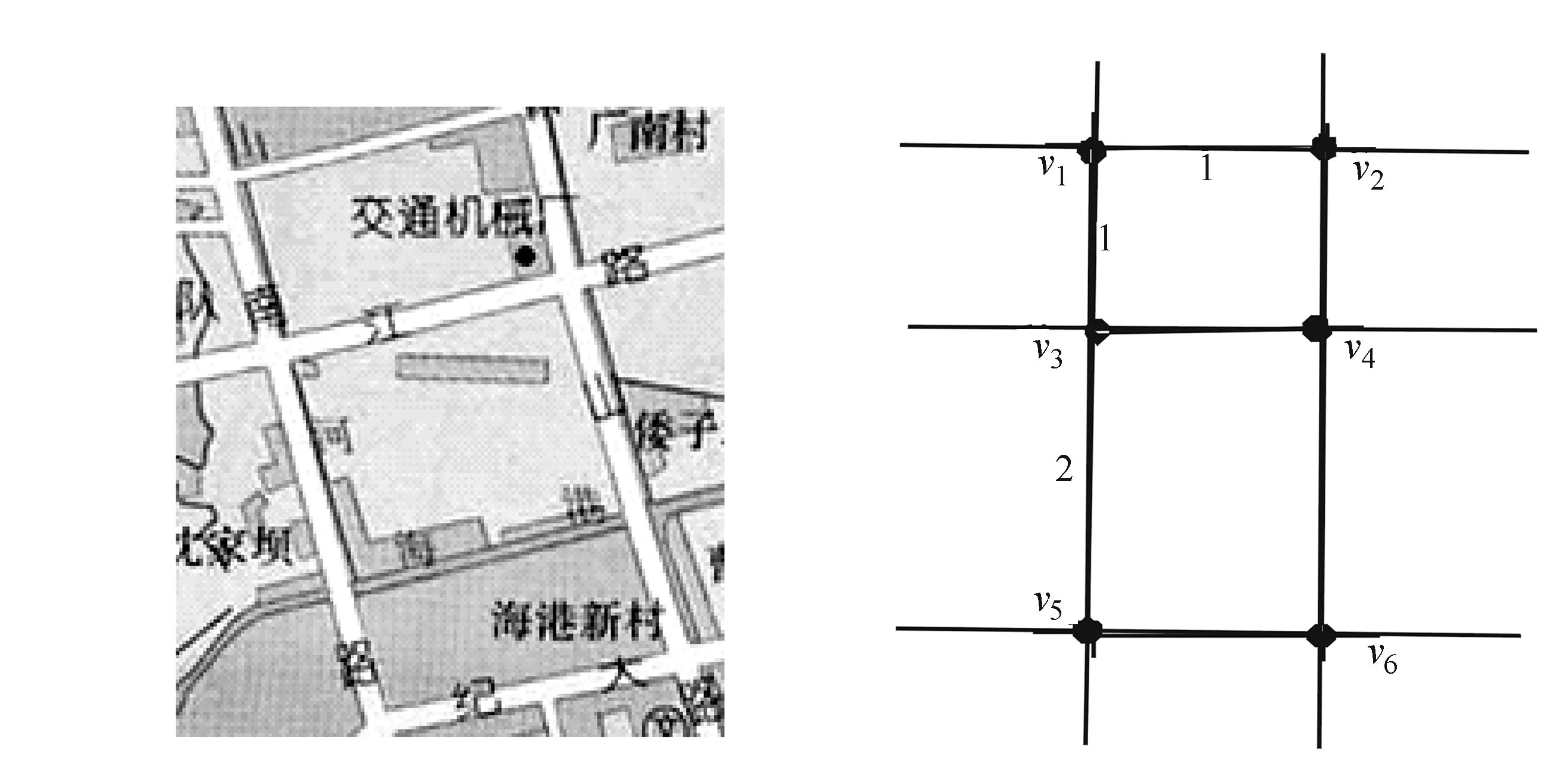
XNET(i,1)≤XNET(i,j) 由定义1可知,(vi,vj)的运输堵塞成本指标为: 同理,(vi,vj+1)的运输堵塞成本指标为: 图1 点对(vi,vj+1)网络示意图 则: 即得到: XNET(i,j+1)≥XNET(i,j) 以此类推: XNET(i,j+2)≥XNET(i,j+1)XNET(i,j)≥XNET(i,1) 所以: XNET(i,1)≤XNET(i,j) 对给定的一个交通网络G(V,E),在G中任意去掉一条边后仍然连通,令N(vi)为vi的邻接节点集合,N(vi)={vi1,vi2,…,vid(i)},其中,d(i)为vi的度,假设Cij为点对(vi,vj)的单位运输成本,且Dij和Dij+1服从某种随机分布,则运输堵塞成本指标的计算步骤如下: 步1 对任一节点vi应用Dijkstra标号法[1]计算vi到任一节点vj的最短路径Pij和最短路径长度S(Pij),其中j=1,2,…,N-1。 步4 重复步1到步3,取i=1,2,…,n-1,i≠j,即可得到: 图2 南通市局部地图 图3 南通市局部地图抽象图 利用上述算法,对江苏省南通市中某区域(见图2)进行运输堵塞成本的计算,假设该市某局部路网在[0,t]时间内,运输量服从正态分布Cij=1,计算该南通市局部路网的运输堵塞成本指标。 表计算结果 由计算结果可知,在南通市该区域里每条路径都有可能不可恢复的堵塞情况下,车辆将比没有发生堵塞的情况下多付出40个单位的运输成本。 从道路交通规划部门的实际需求出发,对交通网络的运输堵塞成本进行了分析和研究。首先分别给出了任意起止点对、一条路径上和整个交通网络上运输堵塞成本指标,然后给出了相关指标的具体算法,最后以南通市某区域为例计算其运输堵塞成本指标。结果表明,在该市某区域每条路径都可能堵塞且堵塞不可恢复的情况下,车辆比没有发生堵塞情况下多付出40个单位的运输成本,从而为道路交通规划部门改善城市交通网络性能提供了参考。 [1]苏兵,徐寅峰.居住和单位小区对方格网络交通边界度的影响分析[J].系统工程,2006,24(12):33-39. [2]金莹,吴敬东.基于网络技术的交通运输成本研究[J].现代经济信息,2009(9):183-184. [3]Nardelli E,Proietti G,Widmayer P.A faster computation of the most vital edge of a shortest path between two nodes[J].Information Processing Letters,2001,79(2):81-85. [4]Su Bing,Xu Qing-chuan.Finding the anti-block vital edge of a shortest path between two nodes[J].Journal Combinatorial Optimization,2007,16:173-181. [编辑] 李启栋 10.3969/j.issn.1673-1409(N).2012.11.053 TB114 1 A 16731409(2012)11N16103

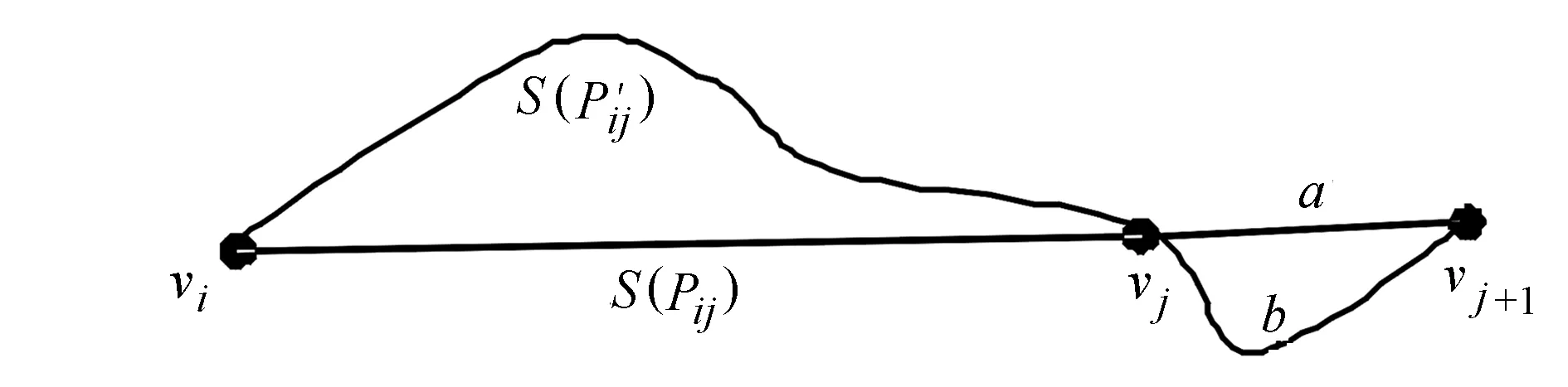




3 运输堵塞成本指标的计算步骤

4 实例计算
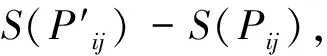

5 结 语

