指派问题的改进蚁群算法研究

王书勤, 黄 茜

(武警警官学院数理系,四川 成都 610213)

指派问题的改进蚁群算法研究

王书勤, 黄 茜

(武警警官学院数理系,四川 成都 610213)

指派问题是组合优化问题的一个分支，也是生活中常见的问题。根据指派问题的特点，将效率矩阵的行标看成旅行商问题的城市，提出了一种改进的蚁群算法，仿真试验结果和其他文献结果比较，证明了该改进算法的可行性。

蚁群算法；旅行商问题；信息素；指派问题

指派问题(Assignment Problem)又称任务分配问题，是一类典型的组合优化问题，同时又是一类常见的NP-Complete问题，它在军事及民用领域都有广泛应用，如火力的最优分配、任务的最优安排、模式分类、工作调度、设备布置、生产安排及印刷电路板设计等，且很多其他组合优化如旅行商问题，工作流问题，车辆运输问题等问题都可以演化成指派问题求解。指派问题一般是用匈牙利法进行计算，但该法很难在计算机上实现[1]，近年来出现了如模拟退火算法、遗传算法 、粒子群算法、神经网络算法等启发式算法为求解任务指派问题提供了新的途径。文献[2]给出了指派问题的遗传算法；文献[3]给出了指派问题的改进粒子群优化算法；文献[4]给出了指派问题的变异蚁群算法。下面，笔者针对指派问题的特点，从另外一个角度提出了一种改进的蚁群算法，对蚁群算法的寻优能力作了一定的探索。

1 指派问题

指派问题描述如下：n个单位，n项任务，一个单位只能受领完成其中的一项任务，一项任务只能交给一个单位，每个单位完成每项任务的效率已知，求使总效率最高的分配。指派问题也叫分派问题，其数学模型为：

用cij表示第i个人完成第j项工作所需的资源数，则效率系数矩阵可表示为C=(cij)n×n。

指派问题既是一个整数规划模型也是一个线性规划模型[5]。

2 蚁群算法

蚁群算法原理是对真实蚁群协作过程的模拟[6-7],算法主要由选择策略、信息素更新和搜索算法组成。算法是根据真实蚂蚁寻找最短路径的方法提出来的，由于蚂蚁会选择信息素浓度大的路径，并在经过的路径上留下信息素，随着时间的推移和信息素的挥发，最短路径上的信息素就会越来越浓，最终使得所有蚂蚁选择该路径，从而找到最短路径。下面以旅行商问题(TSP)为例说明算法的基本框架。

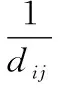
(1)

由i选择j，当所有蚂蚁完成周游环路上的信息素按式(2)或式(3) ：

(2)

(3)

进行全局更新，最后计算每只蚂蚁走过的路径长度，保存最短路径。式中，tabuk为蚂蚁k已访问的城市集合；α和β为信息量和自启发量的权重。

在ant-cycle system模型中:

(4)

M.Dorigo给出了3种算法模型，分别为ant-cycle system, ant-quantity system, ant-density system，其区别就在于式(4)的不同[8]。

3 求解指派问题的蚁群算法设计

3.1 指派问题转化为TSP

指派问题的解是得到一最优指派方案，也就是将单位和任务进行配对，若首先让单位(任务)的次序固定，指派问题就变成了找任务(单位)的最优次序问题，这时可将任务(单位)的序号看成TSP中的城市的序号，将效率cij看成是TSP中蚂蚁所在城市到城市j间的距离，这样就将指派问题转化成了TSP，找到一行标序列或列标序列便得到问题的一个解。

3.2 算法改进

改进的蚁群算法是按从小到大的顺序固定列标，根据效率矩阵让蚂蚁逐列搜索按行标找解，先随机给定蚂蚁第1列的一个行标作为初始解，并将该行标纳入禁忌表，再搜索第2列得到下个行标，直到搜索完所有列，得到所有行标的一个序列，也就找到问题的一个解。根据指派问题的特点，算法主要作了以下改进。

1)动态设置算法参数 为使算法在迭代初期进行广泛的搜索，中期既广泛搜索又做到一定的收敛，后期做到较快收敛，将迭代次数分3段，对参数Q、ρ、α、β、q0进行了动态设置。

2)选择概率的改进 将TSP中选择概率中的自启发因子ηij定义为1/cij(这里指最小化问题)，这样cij越小，ηij越大。

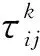
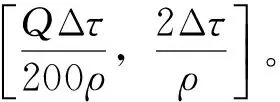
5)最优解检验方式的改进 计算蚂蚁k所得路径上的总效率ck，根据总效率最小原则改进保存最优解。

根据以上对算法的改进和算法的基本思想，算法流程图如图1所示。

4 仿真试验

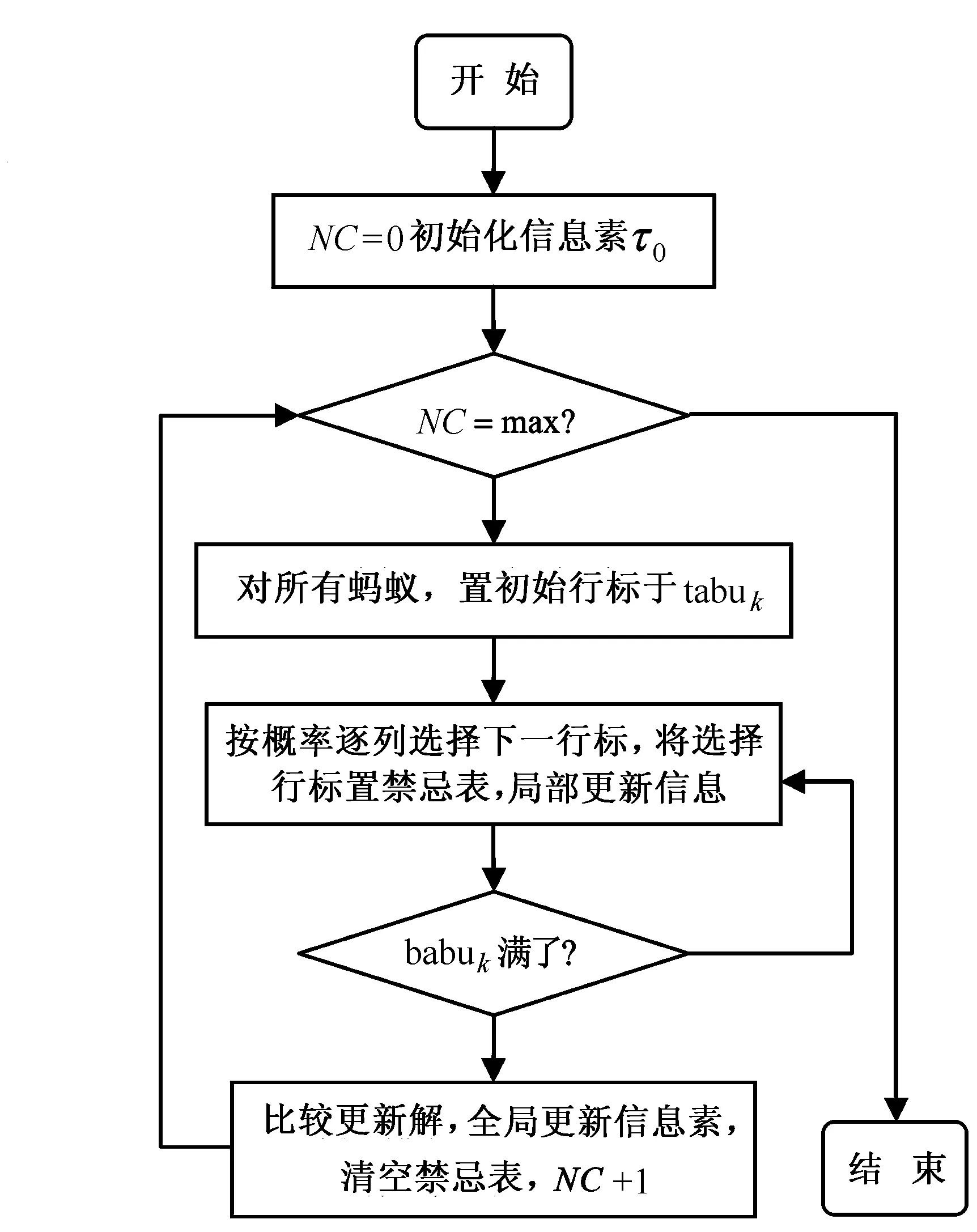
图1 算法流程图

算例1[9]5个工件分配到5台机床上，效率矩阵为

迭代200次，从图2可以看出算法每一次均得到问题最优解，最优行标序列为(5,2,3,4,1)，仿真结果及比较如表1所示，最优值与文献[2]结果相同。

算例2[10]10个任务分配给10台机器，效率矩阵为：

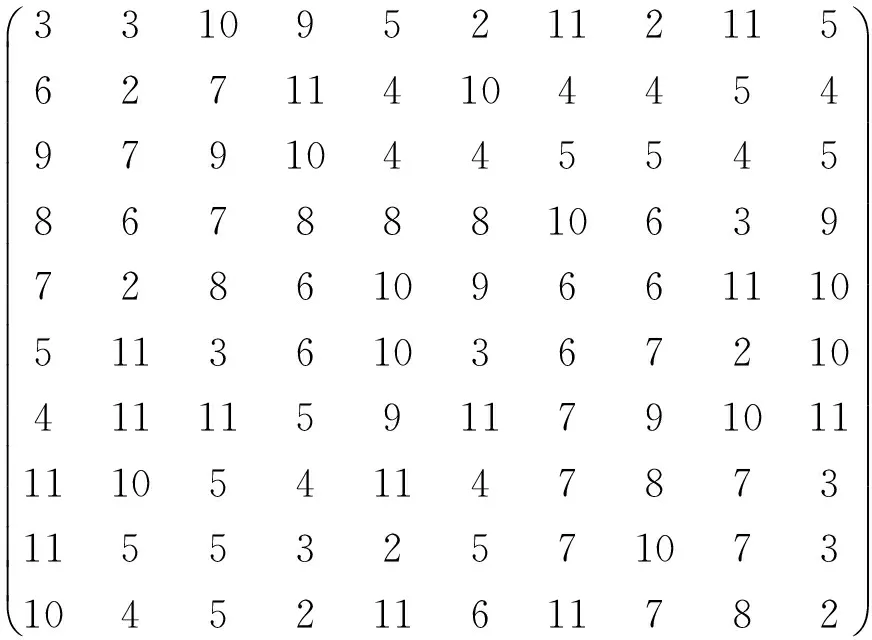
迭代200次，从图3可以看出算法迭代到第78次得到问题最优解，得最优行标序列(7 ，5， 6 ，10， 9 ，3 ，2 ，1， 4， 8)，仿真结果及比较如表2所示，最优值比文献[10]结果略好。

表1 算例1最优解比较表

表2 算例2最优解比较表

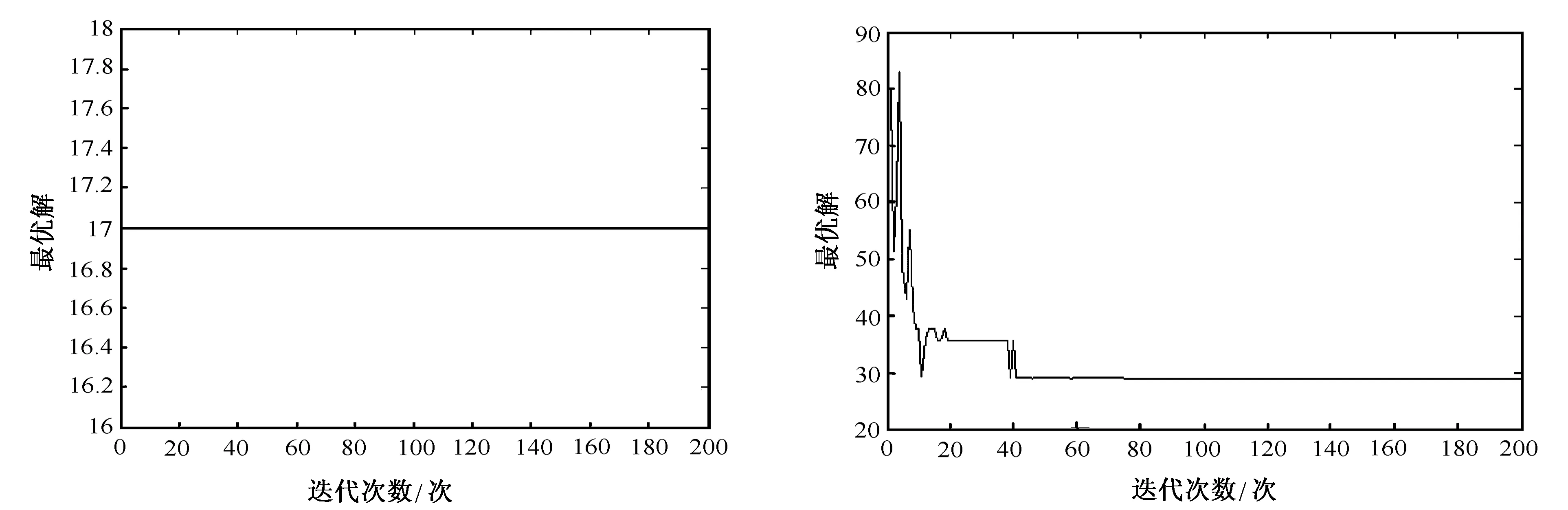
图2 算例1最优值收敛曲线图 图3 算例2最优值收敛曲线图

5 结 语

通过将指派问题与TSP联系起来，提出了一种改进的蚁群算法。实例仿真证明算法大规模问题求解上存在耗时长的缺点，但算法显得简单有效，是一种求解小规模指派问题的非常好的算法之一。

[1] Sukkarieh S, Nebot E M, Durrant-Whyte H F.A High Integrity IMU GPS Navigation Loop for Autonomous Land Vehicles Applications[J].IEEE, 1999, 15(3):572-578.

[2] 李言,陈祖安,徐跃飞,等.指派问题的遗传算法研究与实现[J].西安理工大学学报,1996(4)：271-276.

[3] 谈文芳 ,赵强,余胜阳,等.改进粒子群优化算法求解任务指派问题[J].计算机应用,2007(6)：50-52.

[4] 梁耀,覃征,杨利英,等.指派问题的变异蚁群算法求解[J].微电子学与计算机，2006(6):80-83.

[5] 董树军,张庆捷.军事运筹学[M].北京：蓝天出版社，2006.

[6] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005.

[7] Dorigo M, Gambardella L M.Ant colony system: a cooperative learning approach to the traveling salesman problem [J].IEEE Trans on Evolutional Computation, 1997,1(1):53-66.

[8] 秦玲.蚁群算法的改进与应用[D] .扬州：扬州大学，2004.

[9] 李月秋,杨雅琴.最优指派问题的一种新方法[J].高师理科学刊,2008(3)：15-17.

[10] 杨冬,王正欧.改进的蚂蚁算法求解任务分配问题[J].天津大学学报,2004(4)：373-376.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.10.035

TP312

A

1673-1409(2012)10-N113-04