小a卷起千层浪——数学高考复习教学的一次成功创设

● (青田教师进修学校 浙江青田 323900)

小a卷起千层浪
——数学高考复习教学的一次成功创设

●蒋海瓯(青田教师进修学校 浙江青田 323900)

0 引言

教学效率在实施素质教育的今天被赋予了特殊的意义．事实上，新课程改革的首要目标是“增效”，即提高课堂教学的有效性．然而，当前课程改革在课堂教学层面所遭遇到最大挑战、所遭受到最强烈批评的仍然是教学的无效和低效的问题．一些“所谓的情景教学”削弱了学生的“独立感悟”，一些“所谓的启发式教学”堆砌了太多无效的“提问”，一些“所谓的合作学习”变成了无效的“玩耍”，一些“所谓的自主探索”变为了低效的“放养”，“大多的复习教学”演变成了低效枯燥的高难度习题的“演练”．如何着实增强课堂教学与复习的有效性，是新课程改革的现实诉求，更是广大师生的普遍企求.

1 “函数奇偶性复习教学”的一次成功创设

(上课伊始)师：前面我们复习了函数的概念及其基本性质，知道“定义域、对应法则和值域”是构成函数的三大基本要素，其中“定义域”是灵魂，“对应法则”是核心.函数的“定义域和对应法则”一经确定，函数的“值域”也就随之确定了．函数的奇偶性是函数的一个重要性质，大家不妨先回顾一下“函数奇偶性的定义”？

学生集体：如果对于函数f(x)的定义域内任意一个x，若都有f(-x)=-f(x)，那么函数f(x)就叫做奇函数；若都有f(-x)=f(x)，那么函数f(x)就叫做偶函数．

师：对！那么请问同学们：上述定义中的“关键词”是什么，其“核心部件”又是什么？

学生集体：“关键词”是“任意”2字，“核心部件”是“都有f(-x)=-f(x)，或都有f(-x)=f(x)”．

师：很好！“关键词”和“核心部件”又将意味着什么？能不能“用简洁、直白的语言”告诉我呢？

生1：这说明每一个“x”，都对应着一个“-x”，这意味着具有奇偶性的函数的定义域必须关于原点对称，而且每一对“x”与“-x”，它们对应的函数值“都相反”或者“都相等”．

师：好!函数奇偶性的定义语言非常简洁，我们要善于发现“隐藏”在定义背后的“秘密”，努力发掘“包含”在定义之中的“精彩故事”，这是学习数学不可或缺的思想方法.由此我们明白：奇偶性是函数的一个“整体性质”，“定义域关于原点对称”是函数为奇函数或偶函数的一个必不可少的条件．那么从直观上看，奇、偶函数的图像又有什么特征呢？

生2：奇函数的图像关于原点对称，反之亦然；偶函数的图像关于y轴对称，反之亦然．

师：回答正确！事实上，函数奇偶性的定义既是判定函数奇偶性的一个重要方法，也是奇偶函数的一个性质定理．也就是说，若对于f(x)的定义域内任意一个x，都有f(-x)=-f(x)(或f(-x)=f(x))，则f(x)就叫做奇函数(或偶函数)；反之，若f(x)是奇函数(或偶函数)，则对于f(x)的定义域内任意一个x，都有f(-x)=-f(x)(或f(-x)=f(x))．我们要全面、正确理解函数奇偶性的定义，熟练、灵活地运用函数奇偶性的定义解决有关问题．大家一起来看下面的一个问题：

( )

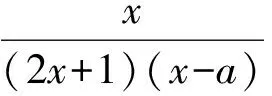
要求：说出求解的具体方法或思路，并作出正确的选择．

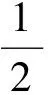
课堂实境此问题一出，立刻引发了全体学生的极大兴趣与积极思索．因为这里“创设的问题”与“平常练习的题目”形式不尽相同(平常的题目大多给出具体的解析式，判断其奇偶性，而这里却含有“参数a”)，就是这样的“一点小小创意”，使“小a的求解”激起了千朵浪花，乃至卷起了千层浪潮，引发了学生的不同见解、热烈讨论乃至激烈的争辩，课堂气氛十分热闹，令笔者欣喜不已！学生思考求解，笔者巡视观察.约3分钟后不少学生已得出了答案，但笔者仍然留给学生更多的思考与探索的时间，并提供给学生进一步思索与求解的空间.约5分钟后，笔者让学生畅所欲言，大胆地发表自己的见解．

生3(自告奋勇)：我是用奇函数的定义求解的，具体过程是(教师将其投影)：由f(x)为奇函数，知

f(-x)=-f(x)，

即

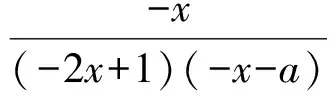
对定义域内所有x恒成立.整理得

-x(2x+1)(x-a)=-x(-2x+1)(-x-a)，

即

x[(2x+1)(x-a)-(2x-1)(x+a)]=0

对定义域内所有x恒成立.化简得

x2(2-4a)=0

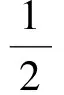
(生3的求解获得相当部分学生的肯定．)

生4(迫不及待)：生3这样做太繁琐了，简直是“小题大做”、“杀鸡用牛刀”了，只要用“特值法”求解即可．由f(-1)=-f(1)，得

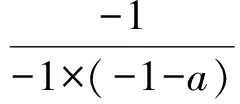
即

3(1-a)=1+a，

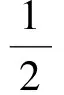
(生4的求解让学生们“大开眼界”，赢得大家的赞赏.但笔者仍然保持沉默，想让学生有更自主的思索与更精彩的灵感.)

生5(心有难言之隐)：生4的想法是不错，能求得a的值，我也是这样做的.但我还有点疑惑，就是仅由f(-1)=-f(1)就能保证函数f(x)一定为奇函数吗？

(学生的思维被有效地调动起来了，学生们继续发言,笔者难以插话.在这里能想到用“特值法”求解已难能可贵了，还想到这一点，更让人刮目相看.看来学生对“奇函数的定义”及其“整体性”已有了一个较充分、较深刻的认识，不会仅由定义域内的某一个x0，满足f(-x0)=-f(x0)，就认定f(x)为奇函数了，这不禁让人欣慰.)

师(终于出言了)：我也有同感哦？特例入手，独具慧眼，简明快捷，令人鼓舞，但这样求得的a值一定能保证f(x)为奇函数吗？同学们可要好好地想一想.

(将问题再度巧妙地“踢还”给学生思考，这是一种教学智慧，更是一种教学艺术.)

生4(再次发言)：这里求得的a只有一个值，当然是所求的答案，否则本题就“没有答案”了！

(理由似乎并不充分，还有点“强词夺理”的味道，难以“自圆其说”，着实“难以服人”呀！)

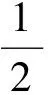
(生5指出了生2断然选C的破绽，但还未正面回答上述“疑问”与“疑惑”．看来答案D的创设，给问题的求解制造了新的困惑，增添了新的思考，笔者期待着学生能有更“合理、完满、令人信服”的解释.)

师(满怀期待)：生5说得有道理,那到底是该选C还是选D呢？大家能给出一个满意的解释吗？

(笔者力图让学生作“深入的思考，正面的回应”，从而及时而圆满地解决这一问题.)

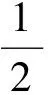
师(脸带微笑)：好的！“特值求解、检验确认”，这的确是一个好方法，现在问题终于得到了完满的解答.

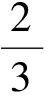
(又出现一种新的求解方法，只是因为答案D的存在，而不能排除到底，所以只能辅之以验证的手段来继续推进)．

师(有感而发)：排除法是解选择题的一种常用方法，但排除法“只能排错的，不能选对的”？

(话音未落，又有学生争着发言.)

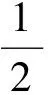
(生8的求解显得快速而智慧，抓住了“定义域”这一灵魂，一举突破，不免让人赏心悦目.)．

师(十分兴奋)：简直是太精彩了！这里“观察、思考、心算、检验”一气呵成，关键是把握住了奇函数定义域的明显特征.同学们还有其他不同的思考与求解吗？请继续畅所欲言吧！

(笔者把问题进一步引向深入，期盼着学生继续自主地思考，主动地出击，得到更多、更广的求解路径.)

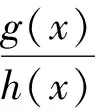
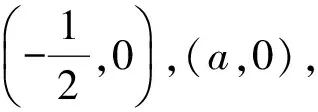
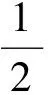
师(喜上眉梢)：同学们表现得真不错！通过主动参与、积极思考、多方探索，不仅发现这么多的求解方法，成功地解决了该问题，而且全面巩固了奇偶函数的性质特点与图像特征，真正地做了一回学习的主人，真是一举而多得啊！

(创设的“问题”在学生轻松愉悦的氛围中自主而高效地圆满解决了.)

2 感悟

有效教学的核心就是教学的效益，即教学有效性是高效、低效还是无效.教学有没有效益，并不是指教师“有没有教完内容”或“教得认不认真”，而是指学生“有没有学到什么”或学生“学得好不好”．如果学生“不想学”或者“学了没有收获”，即使教师教得再辛苦也是无效的教学；同样，如果学生学得很辛苦，但没有得到应有的发展，也是无效或低效的教学.因此，学生有无具体的进步或发展是教学有没有效益的唯一指标．

有效的课堂教学，既包含“教”，更蕴含“学”．教学是否有效很大程度上取决于学生的“学”，有效的教学需要每一个学生脑、手、心的协调配合和有机参与，需要学生动脑、动口、动笔的实际操作，是学生全身心地积极投入．如果学生能自觉地积极参与学习，能发自内心地自主参与学习，并能在学习过程中进行有效地自我调控，那就是一场成功的有效教学活动．

有效的课堂教学，是师生双边的有效互动与学生主动活动的有机结合．教师要正确处理好“教”与“学”双边的和谐关系，要具有诱导学生使其“想学”、指导学生让其“会学”、引导学生令其“能学”的技能，努力使教学过程成为学生积极参与的愉悦生活和情感体验，因为学生越来越爱学习是学习有效性的内在保证．

教师在追求有效教学的同时，要有节约意识，即教学的材料要精简、教学的语言要精炼、教学的手段要精要、教学的训练要精当.教师更要有反思意识，不断地反思自己的日常教学行为，努力提升自身的教学艺术，从而实现有效教学“提高学习效率、增进学习结果、强化学习体验”这三大目标．

[1] 罗增儒.发扬传统优势的“充分条件与必要条件”教学[J].中学数学教学参考，2008(11)：23-27.

[2] 蒋海瓯．我们该如何来“玩”数学——“充分条件与必要条件”课例[J]．中学数学教学参考，2008(11)：16-21.

[3] 蒋海瓯．给足思考时间架设思维空间，引发学生有效参与教学过程[J]．数学教学通讯：教师版，2007(12)：10-11.