有釉陶瓷砖铅溶出量测定的不确定度评定＊

王 智 张卫星 李文清

（国家建筑卫生陶瓷质量监督检验中心 陕西 咸阳 712000）

有釉陶瓷砖铅溶出量测定的不确定度评定＊

王 智 张卫星 李文清

（国家建筑卫生陶瓷质量监督检验中心 陕西 咸阳 712000）

通过分析影响铅溶出量测定的因素，建立数学模型以及计算不确定度分量，确定总的不确定度，最终得到有釉陶瓷砖铅溶出量测定的不确定度，以满足校准、评估及监测工作的需求以及客户对该实验精度的要求。

数学模型 铅溶出量 不确定度

前言

随着科学技术的发展和检验技术的进步，人们对检验结果或数据的准确性和可靠性提出了更高的要求。测量不确定度表明了检验结果或数据的可信赖程度，是测量结果质量的重要指标。测量不确定度的评定和表示方法的采用，是计量科学的一个新进展，是科技交流和国际贸易进一步发展的要求，它使得各国进行测量所得到的结果可以直接进行相互比较，与传统的误差理论相比较，更具有可操作性。在国家实验室认可工作中，GB／T 27025－2008《检测校准实验室能力的通用要求》和ISO／IEC 17025《检测校准实验室能力的通用要求》标准规定，检测实验室应该有能力对所有的检测结果进行不确定度的评定。

1 测定目的

按照GB／T 3810.15－2006《陶瓷砖试验方法第15部分：有釉砖铅和镉溶出量的测定》规定，用原子吸收光谱法测定有釉陶瓷砖中铅溶出量，通过分析影响铅溶出量测定的因素，建立数学模型以及计算不确定度分量和总量，从而评定陶瓷砖釉中铅溶出量测定结果的不确定度。

2 测定步骤

1）样品在（20±2）℃进行处理，处理方法为洗净砖表面并用干布擦干，把6mm宽的硅酮密封胶涂于围绕釉表面的整个周边，并高出釉面以上4mm，让密封胶干燥一个晚上，测量样品的表面积。如本试验样品的表面积为2.37dm2（表1和表2包含了本例的实验数据）。

2）在（20±2）℃条件下将体积分数为4%的醋酸溶液倒入经预处理的样品中，使溶液的液面低于样品上硅酮密封胶溢出釉面1mm，可从样品硅酮密封胶上端边缘处测量。

3）记录使用体积分数为4%的醋酸溶液的体积，精确至±2%（本试验中使用了332mL醋酸）。

4）样品在（20±2）℃的条件下放置24h，并采取适当的措施防止挥发损失。

5）放置后，搅拌溶液使其足够均匀，取一部分溶液待测，如果需要时进行稀释（稀释系数为d），选用合适的波长在原子吸收分光光度计上进行分析测试，应用实验室所确定的最小二乘法校正曲线。

6）计算结果。计算出在总浸泡溶液中铅的含量，用每平方分米表面积含多少毫克铅或用每升体积含多少毫克的方式表示。

3 建立数学模型

通过分析发现影响铅的溶出量测定的因素有：稀释浓度、溶液体积、环境温度、浸泡时间和酸浓度。

稀释后醋酸溶液中铅的浓度C0用原子吸收分光光度计测定，计算公式为：

式中：C0——浸泡液中铅的浓度，mg／L；

A0——浸泡液中金属的吸光度；

B0——校准曲线的截距；

B1——校准曲线的斜率。

对于本试验中，要求结果用每单位面积溶出铅的质量r来表示。r的计算公式为：

式中：r——每单位面积溶出的铅的质量，mg／dm2；

VL——溶出的体积，L；

av——容器的表面积，dm2；

d——样品稀释的系数。

鉴于此方法目前尚未有证标准物质用于评估实验室的操作，因此所有可能的影响因素都要考虑，如稀释浓度、溶液体积、环境温度、浸泡时间和酸浓度。考虑到酸浓度、浸泡时间、环境温度的影响校正因子，其数学计算模型为：

备注：该方法所允许的温度范围是一个不确定度分量来源，这是由于被测量技术规范不完善而产生的。尤其要注意不同操作温度引起的结果变化，因为是按照规范要求测试而得到的结果，因此不能片面地认为是偏差。

4 计算不确定度分量

这个步骤的目的是对先前识别的产生不确定度的每一个来源进行量化。可以用实验数据或基于很好的假定来进行量化。

4.1 稀释系数d

对于目前这个试验，无需稀释浸出溶液，因此不用考虑其对不确定度的影响。

4.2 体积VL

1）填充体积。经验方法要求样品被溶液填充至“距离边缘1mm以内”。对于该实验一般所用的样品，1 mm将代表样品高度的1% 。因此样品被填充的体积为（99.5±0.5）%（即是样品体积的0.995±0.005）。

2）温度。环境温度必须在（20±2）℃，由于与样品相比，液体具有更大的体积膨胀，这样的温度范围会导致体积测量的不确定度。假定温度为矩形分布，则332mL体积的标准不确定度为：

3）读数。记录体积VL要求的准确度在2%范围内，实际上使用量筒时允许约为1%的不准确性（即0.01VL）。假定以三角形分布来计算标准不确定度。

4）校准。体积校准是根据制造商的技术规格进行的，500mL量筒有±2.5mL的偏差。假设以三角形分布来计算不确定度。

本试验中体积为332mL，4个不确定度分量按下式合成：

4.3 铅的浓度C0

使用手工操作的校准曲线计算溶出铅的含量。从（500±0.5）mg／L铅的标准溶液中配制5种标准溶液，其浓度分别为0.1mg／L、0.3mg／L、0.5mg／L、0.7mg／L、0.9mg／L。使用线性最小二乘法拟合曲线程序的前提是假定横坐标的量的不确定度远小于纵坐标的量的不确定度，因此通常的C0不确定度计算程序仅仅与吸光度不确定度有关，而与校准溶液不确定度无关，也与从同一溶液中逐次稀释产生的不确定度无关。然而在本例中，校准标准溶液的不确定度足够小，以至可以忽略。

5个校准标准溶液分别被测量3次，其结果见表1。

表1 校准结果

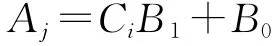
式中：Aj——第i个校准标准溶液的第j次吸光值，mg／L；

Ci——第i个校准标准溶液的浓度，mg／L；

B1——斜率；

B0——截距。

B0、B1的值及其标准偏差如表2所示。

表2 B0、B1的值及其标准偏差

线性最小二乘法拟合曲线的结果其相关系数r为0.997，残差标准偏差S是0.005 486。

实际为溶出溶液2次，浓度C0为0.26mg／L。最小二乘法拟合曲线程序有关的不确定度u（C0）的详细计算参见《化学分析中不确定度的评估指南》，因此这里只是简述不相同的计算步骤。

校准曲线为：

残差标准偏差为：

以及

式中：B1——斜率；

P——测试C0的次数，次；

n——校准的次数，次；

C0——溶出液中铅的浓度，mg／L；

C——不同校准标准溶液浓度的平均值（n次），mg／L；

i——下标，指校准标准溶液的数量；

j——下标，指获得校准标准曲线的测量次数。

4.4 温度影响因素ftemp

相关文献表明，针对温度对有釉砖产生的影响已经做过一些研究。一般来说，温度对其影响相当大，并且随着温度的变化，溶出的金属呈上升趋势，直至达到极限值。只有一个研究给出温度范围（20～25℃）的影响。从研究在25℃附近溶出的金属与温度变化的图形资料看是接近于线性，其斜率约为5%C－1。经验方法允许±2℃的范围导致温度系数ftemp为1.0±0.1。假定为矩形分布，将其转换为标准不确定度分量：

4.5 时间影响因素ftime

对于相对较慢的过程，入浸泡过程，溶出量将大约与时间的微小变化成正比。KRINITZ和FRANCO发现在浸泡过程的最后6h中，浓度的平均变化在86mg／L时大约是1.8mg／L，即约为0.3%／h，因此对于（24±0.5）h的浸泡时间，C0需要用系数ftime进行修正：1±（0.5×0.003）＝1±0.001 5。这是矩形分布，产生的标准不确定度为：

4.6 酸浓度facid

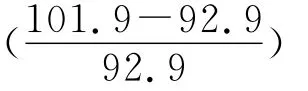
4.7 计算合成标准不确定度

假定没有稀释，则每单位面积溶出铅的含量为：

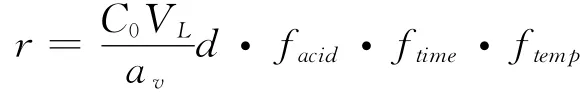
中间值和标准不确定度被收集于表3中，将这些数据代入式中，得到：

为了计算合成标准的不确定度，将每个不确定度分量代入下式，得到：

表3 铅溶出量测定的不确定度

5 计算总不确定度

总不确定度u（r）通过使用范围因子2计算得到：

6 结论

在有釉陶瓷砖铅溶出量的不确定度的评定过程中，每一分量对于合成不确定度的作用都要进行评估，不一定所有分量都会对合成不确定度有重要作用，通过分析各分量与合成不确定度之间的关系，选取主要的分量。可根据实际情况采取相应的措施，保证测量结果的准确性和可靠性。

笔者提供了一种确定重金属溶出量测试时评定其不确定度的较为实用的解决思路，希望能对类似测量中的不确定度评定提供参考。

1 国家质量技术监督局计量司.测量不确定度评定与表示指南.北京：中国标准出版社，2001

2 中国实验室国家认可委员会.化学分析中不确定度的评估指南.北京：中国计量出版社，2002

3 李文清，温伟明，等.陶瓷样品中铅含量测定的不确定度评定.全国建材科技核心期刊——《陶瓷》，2011（5）：31～32

4 李晓燕.现代仪器分析.北京：化学工业出版社，2008

TQ174

B 文章标识码：1002－2872（2012）03－0034－03

王智（1983－），本科，助理工程师；主要从事检测与质量管理工作。