iGPS测量场精度分析及其应用研究
杜福洲, 陈哲涵, 唐晓青
北京航空航天大学 机械工程及自动化学院, 北京 100191
iGPS测量场精度分析及其应用研究
杜福洲*, 陈哲涵, 唐晓青
北京航空航天大学 机械工程及自动化学院, 北京 100191
为了支持iGPS测量系统在航空、航天、船舶等大型复杂产品装配过程中的布局优化和系统选型,提高测量效率和精度,对其测量精度分布规律进行了研究。阐述了iGPS测量系统的工作原理,构建了其计算机仿真模型;根据其布局形式的特点,提出了iGPS测量单元与测量网络的概念;给出了一种iGPS测量场精度分析方法,并通过实例对测量单元和测量网络的测量场精度与发射器布局及目标点空间位置间的量化关系进行分析。试验结果表明,当发射器间距为20 m时,iGPS测量场的测量精度在垂直方向上的波动范围在0.01 mm内,在水平方向上测量精度呈线性变化,最高测量精度为0.12 mm,出现在测量场的中心,最低测量精度为0.25 mm,出现在测量场的边界处。在iGPS测量场精度分析的基础上,提出了一种基于精度约束的测量方案评估方法及其实施步骤,为iGPS测量系统的选型和工程应用提供支持。
iGPS; 测量系统精度分析; 单元测量场; 网络测量场; 测量方案评估; iGPS布局优化
随着航空、航天、船舶等大型产品部件装配及大部件对接装配对精确定位、实时位姿测控、最终装配质量的准确评定要求的日益提高,激光跟踪仪、激光雷达及iGPS等大尺寸空间数字化测量系统及其应用技术受到工业界和学术界的广泛关注[1-2];与其他大尺寸空间测量系统相比,iGPS测量系统具有测量范围可近似等精度扩展、测量精度较高、无需断光续接、支持并行测量等优势,已成为当前大尺寸空间测量技术的一种发展趋势[3]。波音、空客、洛克希德·马丁等国外航空航天制造企业较早开展iGPS测量系统在柔性装配型架安装、大型部件精确定位以及自动钻铆机末端执行器位置标定等过程中的应用研究[4-9],以缩短装配周期,提高装配质量。例如,美国AIT公司在为B787建立的数字化自动对接装配平台中使用iGPS测量系统实现POGO柱的标定以及机身与机翼的定位[10];F35在装配过程中采用iGPS测量系统精确引导AGV(Automated Guided Vehicle)的移动。目前,随着国内数字化装配技术的发展,相关学者及航空航天企业也逐渐展开了iGPS测量系统的相关技术与工程应用研究[11]。
iGPS测量系统的应用,需要确定发射器的数量和布局形式,同时应满足测量精度、测量范围、测量效率以及测量成本等方面的要求,因此,对给定布局形式的iGPS测量场的精度分析成为实现其布局优化和系统选型的关键技术。文献[12]对iGPS测量系统单个发射器的角度测量不确定度进行了研究,给出单发射器角度测量不确定度与测量空间及目标点位置间的量化关系曲线;文献[13]和文献[14]对iGPS测量系统的整体性能进行了研究,分析iGPS发射器数量与其测量不确定度的关系,并指出iGPS测量系统在动态测量方面的缺陷;文献[15]分析了iGPS测量系统的精度与发射器数量、姿态及相互位置等因素的关系,并指出当发射器间距离小于20 m时,其测量精度较高。
综上所述,目前对iGPS测量系统的基础研究主要围绕其静态、动态测量特性以及误差源分析等方面展开。本文在已有研究的基础上,提出iGPS单元测量场与网络测量场的概念,给出一种基于单元测量场的iGPS精度场分析方法及其仿真实现,并通过实例研究iGPS测量场精度特性与发射器布局间的量化关系以及基于精度约束的测量方案评估方法,为iGPS测量系统的选型和工程应用提供支持。
1 iGPS工作原理、系统建模及测量场定义
1.1 工作原理
iGPS测量系统主要由发射器、有线/无线传感器(接收器)以及控制系统3部分组成[16],其工作原理如图1所示。发射器分布在空间的不同位置,产生LED脉冲信号和扇形激光平面信号两类光信号;传感器放置在待测点处,接收到发射器所发出的光信号,并将其转换成电信号,控制系统将电信号转换为不同的时间数据,基于不同发射器的转速与频率解算出待测点的空间坐标。

图1 iGPS测量系统工作原理Fig.1 Working principle of iGPS measurement system
1.2 系统建模
根据iGPS工作原理构建其理论测量模型如式(1)所示:
(1)
式中:P为目标点坐标的测量结果;P0为目标点在全局坐标系下的理论位置;θ为目标点在局部坐标系下的角度数据;TS为发射器的布局形式。
在测量过程中,由于发射器的制造和安装误差(轴线的垂直度、激光平面的夹角等)、测量环境(温度、湿度、空气折射率等)以及传感器灵敏度、振动、控制系统电路的零点漂移等因素的影响[12,17],传感器接收到的光信号与理论值存在差异,导致目标点在各发射器局部坐标系下的角度数据计算结果产生误差,最终造成坐标测量结果的误差。因此,在式(1)所示的理论模型基础上引入角度测量随机误差:δθi~U(0,σ2),依据现有的iGPS测量系统出厂参数将σ取为2,对应的设备为Nikon iSpace系统[18]。
基于以上的分析,建立iGPS测量系统的仿真测量模型如式(2)所示,通过对目标点P的重复测量结果进行正态分布拟合,得到测量场在目标点处的测量不确定度σP,作为其精度指标;σP的值越大,则测量精度越低;反之,则测量精度越高。
(2)
1.3 测量场定义
现有研究表明[13-14],当发射器数量超过4个时,继续增加发射器的数量对测量系统的精度不会有显著影响,基于测量经济性的考虑,本文将4个发射器构建的测量系统称为iGPS测量单元,相应的测量场称为单元测量场(如图2(a)所示);通过多个测量单元的连接和组网,构成iGPS测量网络,相应的测量场称为网络测量场(如图2(b)所示),以实现测量范围的扩展。
由图2可见,外围发射器形成的边界将测量场分为内测量场和外测量场两部分,由于发射器产生的光信号强度随着距离的增大而衰减,外测量场的光信号强度将越来越弱,导致其测量误差的增大;以两个发射器间距离的一半作为外测量场的最大有效测量范围,该有效测量范围与内测量场共同形成iGPS测量系统的有效测量场。
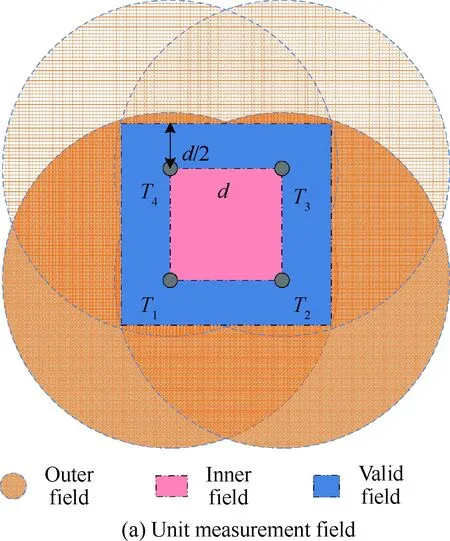
图2 iGPS测量场定义Fig.2 Definition of iGPS measurement fields
有效测量场作为iGPS测量系统的一项属性,表达了测量系统处于有效工作状态的测量空间,在实际应用中,被测对象应尽量置于有效测量场中,以提高测量精度。
2 iGPS单元测量场精度分析
基于图2(a)所示的iGPS测量单元布局形式构建单元测量场精度分析模型,如图3所示,设发射器间距d=20 m,建立测量场全局坐标系,则发射器布局形式如表1所示。

图3 单元测量场分析模型Fig.3 Analysis model of unit measurement field
表1 单元测量场发射器布局形式Table 1 Transmitter layout of unit measurement field

m
2.1 全局精度分析
对图3所示的iGPS测量场进行均匀的网格划分,令Px=0∶2∶40,Py=0∶2∶40,Pz=0∶10,得到4 851个目标点,基于仿真iGPS测量系统模型对各点进行测量,得到各点的精度分布特性如图4所示。
由仿真测量结果可见,在图3所示的发射器布局形式下,单元测量场的全局测量精度范围为0.130~0.425 mm左右。在同一高度上,测量精度的水平分布规律相似,均以测量场中心线与水平面的交点(x=y=20 m)为圆心呈同心圆状分布,且距离中心线越远时测量精度越低。由于发射器测量范围的俯仰角度限制,在各发射器附近的点只能被其他3个发射器测量,因此测量精度在该区域内出现“奇点(Singular Point)”,导致精度等高线不连续。在不同高度上,与测量场中心线的距离相等的各点测量精度波动较小。

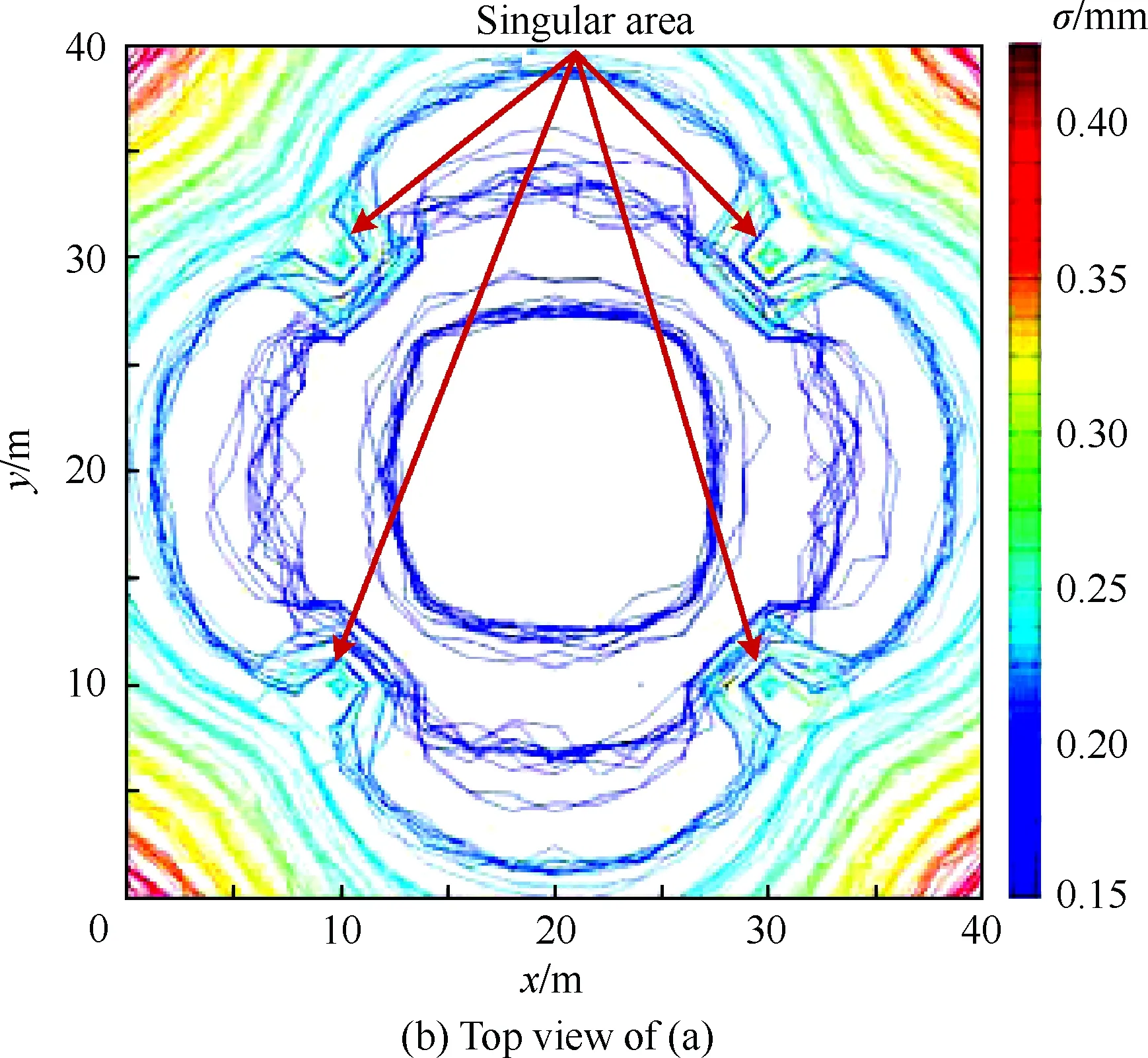
图4 单元测量场全局精度特性Fig.4 Global precision characteristic of unit measurement field
由于测量不确定度存在一定的随机性,上述试验结果的精度值可能存在较大误差。为了对测量场精度特性进行更精确的分析,基于上述单元测量场的全局精度分布规律,将其精度特性分为纵向与横向两个维度进行研究:纵向精度特性是指经过测量场中心线的任意垂直面上的测量精度分布规律;横向精度特性是指测量场内任意水平面上的测量精度分布规律。
2.2 纵向精度分析
选取经过测量场中心线且平行于xOz平面的垂直面(y=20 m)作为纵向精度特性分析的对象,目标点的x坐标反映了其与测量场中心线的距离。通过仿真试验得到目标点高度变化时其坐标测量精度的变化规律,如图5(a)所示。
试点地区率先建立水资源管理责任与考核制度,落实水资源管理行政首长负责制。7个省级试点全部建立了由省政府一把手负总责、分管领导为具体责任人、水利厅(局)长任联络员的水资源管理责任制并逐级落实管理责任。山东省把最严格水资源管理制度考核结果作为各市水利工作的总体评价依据,并与各市科学发展综合考核挂钩。深圳市在对各区政府考核的同时,将市发改委、财政局、国土规划局等相关政府职能部门纳入考核范围,促进各部门协调配合。
仿真结果表明,在经过测量场中心线的垂直面上,目标点坐标测量精度随高度变化而波动的幅度较小,不超过0.01 mm。在与测量场中心线平行且相距一定距离的垂直线上(如x=10 m,y=20 m),目标点测量精度与其高度近似呈二次曲线关系,以发射器所在的高度为极值点对称分布,且与发射器高度差越大,其坐标测量精度越高,因此在实际应用过程中,通常将发射器安装在工作空间(如厂房)靠近顶部的位置,以提高测量精度。图5(b)为以x=10 m时的曲线为例,使用最小二乘法进行拟合,得到测量精度与目标点相对发射器高度差的关系曲线,其表达式为
σx=10,y=20,z=-0.000 43Δz2+0.171
综合距测量场中心线不同距离的目标点坐标测量精度变化规律,将上述关系方程推广至一般形式,得到单元测量场纵向精度特性方程:
σL,z=AL(z-zT)2+σL,zT
(3)
式中:AL为小于0的系数,称为iGPS单元测量场纵向精度特性系数,反映了测量场垂直方向上的测量精度变化率,且由目标点到测量场中心线的垂直距离L确定;z为目标点高度,zT为发射器高度,均以m为单位,只取其数值,无物理意义;σL,zT为目标点处在与发射器同一高度上且与测量场中心线相距为L时的坐标测量不确定度,即测量精度指标的量化值,以mm为单位。

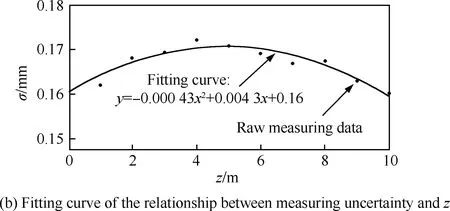
图5 单元测量场纵向精度特性Fig.5 Vertical precision characteristic of unit measurement field
2.3 横向精度分析


图6 单元测量场横向精度特性Fig.6 Horizontal precision characteristic of unit measurement field
仿真结果表明,在水平面上,目标点的坐标测量精度与其到测量场中心线的距离呈线性关系,拟合得到其关系方程如下:
σL,zT=0.004 5L+0.12
同样地,将上述关系推广到一般形式,得到发射器所在的水平面上目标点坐标测量精度特性方程为
σL,zT=BdL+Cd
(4)
式中:Bd和Cd称为单元测量场横向精度特性系数,由各个发射器间的距离确定,Cd反映了单元测量场发射器水平面的最高测量精度,Bd反映了测量场水平方向上的测量精度变化率。
2.4 综合精度分析
基于2.1~2.3节仿真测量试验结果与分析,根据式(3)和式(4)得到单元测量场综合精度特性方程:
σL,z=AL(z-zT)2+BdL+Cd
(5)
式中:d为发射器间距离,zT为发射器高度,二者共同反映了单元测量场的测量方案。
由式(5)可见,单元测量场的精度特性由其布局形式唯一确定,最低精度出现在发射器水平面的边界处:
σmax=Bdd+Cd
最高精度出现在测量场中心线的边界处:
上述σmax、σmin、Bd、Cd4个参数称为反映单元测量场精度特性的关键精度参数。当采用图3所示的布局形式时,iGPS单元测量场的精度特性可表示为
σL,z=-0.000 43(z-5)2+0.004 5L+0.12
3 iGPS网络测量场精度分析
由于航空、航天、船舶等产品尺寸较大,测量单元所形成的单元测量场难以同时满足其数字化测量的精度和范围要求,因此需要基于测量单元构建iGPS测量网络,在满足测量精度要求的同时实现测量范围的扩展。


图7 网络测量场布局形式Fig.7 Layout of network measurement field
由第2节的分析已知,σmax、σmin、Bd和Cd为反映测量场精度特性的4个关键参数,通过仿真测量试验得到网络测量场的发射器数量N(或单元测量场数量M)与测量场关键精度参数间的量化关系如图8所示。
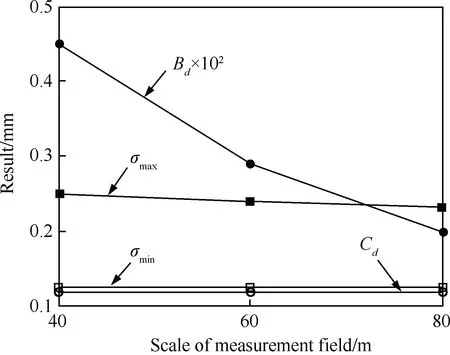
图8 网络测量场关键精度参数与发射器数量间的关系Fig.8 Relationship of key parameters and transmitter number of network measurement field
图8的计算结果表明,随着单元测量场数量的增加,测量范围显著增大,测量场的最高测量精度基本不变,但最低测量精度逐渐提高,其测量精度变化率显著下降。因此,iGPS网络测量场在大幅度扩展测量范围的同时,能够保持测量精度的稳定性,同时,式(5)所示的单元测量场精度特性方程同样适用于网络测量场。
4 基于精度约束的测量方案评估方法
基于iGPS的大型产品数字化装配过程测量方案包括两部分:①iGPS测量网络的布局形式决定了网络测量场的精度特性;②待测产品在网络测量场中的位置和姿态决定了待测目标点所处位置的测量精度能否满足测量任务的精度要求。由于iGPS测量系统安装过程比较复杂,且测量成本较高,通常在完成安装后不轻易改变其测量方案;因此,在安装之前需要对测量方案进行评估和优化,使其满足数字化测量任务的精度要求。
传统的测量方案评估过程通过验证法实现,即首先给定测量方案,进而基于iGPS测量场的精度特性方程计算各个待测目标点处的精度,判断其是否满足要求;若所有点均满足要求,则确定该测量方案;否则,修改测量方案重复验证。使用验证法进行测量方案评估的过程操作繁琐,效率较低,难以快速确定合适的测量方案;因此本文提出基于三维仿真环境的精度碰撞法,以实现快速的测量方案评估,其原理如图9所示。
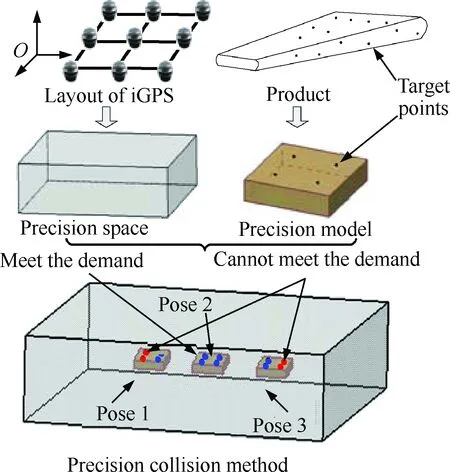
图9 精度碰撞法原理Fig.9 Principle of precision collision method
1) 对于给定的测量方案,根据其中的iGPS测量系统布局形式在三维仿真环境下构建可视化的网络测量场,进而基于式(1)和式(2)所示的iGPS测量系统数学模型和式(5)所示的精度特性方程,得到网络测量场中各点的精度数值,形成iGPS测量系统的精度空间σiGPS。
2) 基于待测产品的三维模型及测量任务的精度要求构建待测产品的精度模型σtarget,并加载到可视化的iGPS网络测量场中。
3) 对待测产品的精度模型与iGPS测量系统的精度空间进行精度碰撞检查:
ifσiGPS<σtarget, colour=GREEN;
else colour=RED。
在三维仿真环境中调整待测产品精度模型的位置和姿态,使得精度模型上所有目标点的颜色显示为绿色,从而得到满足精度要求的待测产品位姿。
4) 若在给定的iGPS测量系统精度空间中无法得到合适的产品位姿,则需要改变发射器间距d或发射器数量N,重新生成精度空间,重复步骤3),直至确定合适的测量方案。
精度碰撞法利用计算机辅助三维图形环境建立可视化测量场,并基于iGPS测量系统数学模型构建精度空间,从而采用人机交互的方式实现测量方案快速评估与优化,以提高iGPS测量系统应用的效率和可靠性,为其在航空产品数字化装配过程中的应用提供了支持。
5 结 论
1) iGPS单元测量场的有效测量范围为2d×2d,在有效测量范围内,其精度特性满足方程:σL,z=AL(z-zT)2+BdL+Cd;iGPS网络测量场可以实现基于单元测量场的近似等精度扩展。
2)d=20 m时,单元测量场的全局测量精度在0.12~0.25 mm范围内;同一水平面上,测量精度等高线以测量场中心线在水平面上的投影点为中心,呈同心圆状分布,且距离中心越远测量精度越低;不同高度上,x、y坐标相同的目标点测量精度波动较小,当d=20 m时,波动幅度小于0.01 mm。
3) 构成网络测量场的单元测量场数量增加(M=1,4,9)时,其测量范围显著扩展,但最高测量精度基本不变,最低测量精度提高的幅度较小,测量精度的变化率Bd显著下降,即其全场测量精度趋于稳定。
4) 基于iGPS测量场精度分析方法,给出了一种基于精度碰撞的测量方案评估方法,为iGPS测量系统在大型产品数字化装配过程中的应用提供支持。
[1] Maropoulos P G, Guo Y, Jamshidi J, et al. Large volume metrology process models: a framework for integrating measurement with assembly planning. CIRP Annals-Manufacturing Technology, 2008, 57(2): 477-480.
[2] Muelaner J, Maropoulos P G. Large scale metrology in aerospace assembly. Proceedings of DET2008, 5th International Conference on Digital Enterprise Technology, 2008.
[3] Zou F, Shang K. Digital measurement world for future factory. Aeronautical Manufacturing Technology, 2008(19): 26-29. (in Chinese)
邹方, 尚可. 未来工厂的数字化测量世界. 航空制造技术, 2008(19): 26-29.
[4] Maropoulos P G, Zhang D, Chapman P, et al. Key digital enterprise technology methods for large volume metrology and assembly integration. International Journal of Production Research, 2007, 45(7): 1539-1559.
[5] Qiu B G, Jiang J X, Bi Y B, et al. Study on posture alignment and joining test system for large aircraft fuselages. Acta Aeronautica et Astronautica Sinica, 2011, 32(5): 908-919. (in Chinese)
邱宝贵, 蒋君侠, 毕运波, 等. 大型飞机机身调姿与对接试验系统研究. 航空学报, 2011, 32(5): 908-919.
[6] Qu W W, Dong H Y, Ke Y L. Pose accuracy compensation technology in robot-aided aircraft assembly drilling process. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1951-1960. (in Chinese)
曲巍崴, 董辉跃, 柯映林. 机器人辅助飞机装配制孔中位姿精度补偿技术. 航空学报, 2011, 32(10): 1951-1960.
[7] Kayani A, Jamshidi J. Measurement assisted assembly for large volume aircraft wing structures. Proceedings of DET2007, 4th International Conference on Digital Enterprise Technology, 2007.
[8] Wang Z, Mastrogiacomo L, Franceschini F, et al. Experimental comparison of dynamic tracking performance of iGPS and laser tracker. International Journal of Advanced Manufacturing Technology, 2011, 56(1-4): 205-213.
[9] Yan Q J. Study on the measuring techniques of the symmetry axes of warhead based on indoor GPS. Harbin: Department of Automatic Test and Control, Harbin Institute of Technology, 2007. (in Chinese)
闫奇瑾. 基于室内GPS的弹头形心轴线测量方法的研究. 哈尔滨: 哈尔滨工业大学仪器科学与技术学院, 2007.
[10] Yu Y, Tao J, Fan Y Q. Assembly technology and process of Boeing 787 jet. Aeronautical Manufacturing Technology, 2009(14): 44-47. (in Chinese)
于勇, 陶剑, 范玉青. 波音787飞机装配技术及其装配过程. 航空制造技术, 2009(14): 44-47.
[11] Xu X D, Chen S, Bi L W, et al. Digital assembly technology for aircraft. Aeronautical Manufacturing Technology, 2008(14): 48-50. (in Chinese)
许旭东, 陈嵩, 毕利文, 等. 飞机数字化装配技术. 航空制造技术, 2008(14): 48-50.
[12] Muelaner J E, Wang Z, Jamshidi J, et al. Study of the uncertainty of angle measurement for a rotary-laser automatic theodolite (R-LAT). Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2009, 223(B3): 217-229.
[13] Maisano D A, Jamshidi J, Franceschini F, et al. Indoor GPS: system functionality and initial performance evaluation. International Journal of Manufacturing Research, 2008, 3(3): 335-349.
[14] Maisano D A, Jamshidi J, Franceschini F, et al. A comparison of two distributed large-volume measurement systems: the mobile spatial coordinate measuring system and the indoor global positioning system. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2009, 223(B3): 511-521.
[15] Zhu Y G, Huang X, Qin L G. Instrllation and calibration of airplane inertial navigation based on indoor GPS. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(5): 615-619. (in Chinese)
朱永国, 黄翔, 秦龙刚. 基于局域GPS的飞机惯性导航部件安装校准. 南京航空航天大学学报, 2009, 41(5): 615-619.
[16] Arc Second. Indoor GPS technology for metrology. Dulles, Virginia: ARCSecond, 2002.
[17] Arc Second. Apparatus and method for determining position: United States Patent, US6501543B2. 2002-12-31.
[18] Nikon metrology. (2011-12-12)[2011-12-12]. http://www.nikonmetrology.com/en_US/Products/Large-Volume-Applications/iGPS.
PrecisionAnalysisofiGPSMeasurementFieldandItsApplication
DUFuzhou*,CHENZhehan,TANGXiaoqing
SchoolofMechanicalEngineeringandAutomation,BeihangUniversity,Beijing100191,China
TosupportthelayoutoptimazationandsystemselectionofaniGPSmeasurementsystemintheassemblyoflargecomplexproductsinaviation,aerospace,shipbuildingandotherindustries,andimprovethemeasuementefficiencyandprecision,thecharacteristicsofitsmeasurementprecisionisstudied.ThispaperpresentsamethodfortheprecisionanalysisandthetransmitterlayoutoptimizationofaniGPSmeasurementsystem.First,theworkingprincipleoftheiGPSmeasurementsystemisinvestigated,andasimulationsystemmodelisconstructed.TheconceptsoftheiGPSmeasurementunitandmeasurementnetworkarediscussed,andaprecisionanalysismethodoftheiGPSmeasurementfieldisstudied.AcasestudyiscarriedoutforanalyzingthequantitativerelationshipbetweenthemeasurementprecisionofaniGPSmeasurementfieldanditstransmitterlayout.Theresultsindicatethat,whenthedistancebetweenthetransmittersis20m,theverticalfluctuationsofmeasurementprecisionislessthan0.01mm,andthehorizontalmeasurementprecisionislinear,themaximumvalueofmeasurementprecisionis0.12mm,whichappearsinthecenterofthemeasurementfield,whiletheminimumvalueofmeasurementprecisionis0.25mm,whichoccursintheboundaryofthemeasurementfield.Finally,aprecisionconstraintbasedmeasuringschemaevaluationmethodanditsimplementationisdevelopedtosupporttheselectionandindustrialapplicationoftheiGPSmeasurementsystem.
iGPS;precisionanalysisofmeasurementsystem;unitmeasurementfield;networkmeasurementfield;measuringschemaevaluation;optimizationofiGPSlayout
2011-11-16;Revised2012-01-10;Accepted2012-02-09;Publishedonline2012-03-051108
URL:www.cnki.net/kcms/detail/11.1929.V.20120305.1108.005.html
NationalNaturalScienceFoundationofChina(50905010)
.Tel.:010-82316795E-maildu_fuzhou@163.com
2011-11-16;退修日期2012-01-10;录用日期2012-02-09; < class="emphasis_bold">网络出版时间
时间:2012-03-051108
www.cnki.net/kcms/detail/11.1929.V.20120305.1108.005.html
国家自然科学基金(50905010)
.Tel.:010-82316795E-maildu_fuzhou@163.com
DuFZ,ChenZH,TangXQ.PrecisionanalysisofiGPSmeasurementfieldanditsapplication.ActaAeronauticaetAstronauticaSinica,2012,33(9):1737-1745. 杜福洲,陈哲涵,唐晓青.iGPS测量场精度分析及其应用研究.航空学报,2012,33(9):1737-1745.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
1000-6893(2012)09-1737-09
V219; TH741
A
杜福洲男, 博士, 讲师。主要研究方向: 数字化测量技术及应用、 质量工程、 质量管理信息化。
Tel: 010-82316795
E-mail: du_fuzhou@163.com
陈哲涵男, 博士研究生。主要研究方向: 大尺度空间测量技术, 数字化测量辅助装配技术及应用。
Tel: 010-82317740
E-mail: cloudy731@163.com
唐晓青女, 教授, 博士生导师。主要研究方向: 制造系统工程, 质量管理与质量工程,先进制造技术。
Tel: 010-82317740
E-mail: tangxq@buaa.edu.cn

