星上光学有效载荷的两级隔振研究
张尧, 徐世杰
北京航空航天大学 宇航学院, 北京 100191
星上光学有效载荷的两级隔振研究
张尧, 徐世杰*
北京航空航天大学 宇航学院, 北京 100191
为实现星上光学有效载荷的高成像性能,对星上光学有效载荷的两级隔振进行了研究。所谓两级隔振,即除了对控制力矩陀螺群(CMGs)等执行机构振动源进行隔振外,还在光学有效载荷和星体之间加入隔振装置。首先建立了含有两级隔振系统以及CMGs和太阳帆板的整星动力学模型,并采用ADAMS工程软件验证了所推导模型的正确性;其次,在合理假设的基础上简化模型,分别求得由扰动源到星体和有效载荷的传递函数矩阵,分析CMGs隔振平台参数变化对姿态控制系统的影响,选择合理参数分析两级隔振系统的频域特性;最后通过数值仿真分析了两级隔振系统在星上应用的可行性,并通过频谱对比分析两级隔振系统对光学有效载荷姿态稳定度的改善程度。
成像质量;光学有效载荷;抖动;动力学;隔振
近年来高精度、高稳定度空间观测设备以及遥感遥测卫星成为航天器发展的一种重要趋势。其上搭载的光学有效载荷对航天器的姿态稳定度以及结构振动水平要求极其严格。1990年发射的哈勃望远镜(HST)指向稳定度为0.007″[1];美国詹姆斯韦伯望远镜(JWST)为了获得接近光学衍射极限的图像,指向稳定度将达到0.005″[2];类地行星探测器(TPF-C),则又进一步把指向精度要求提高了一个量级[3]。
该类航天器在轨运行期间,星上高速旋转部件的振动、变轨调姿期间推力器点火工作产生的扰动、大型柔性结构进出阴影区冷热交变诱发的扰动等都会使星体产生一种幅值较小、频率较高的抖动响应[4]。这其中,大部分扰动可以通过某种方式加以补偿或只是偶尔发生。但是,作为姿态控制执行机构的控制力矩陀螺(CMG)却对航天器的整个工作过程产生持续的扰动。
CMG的振动是由转子静动不平衡以及轴承加工不完整性等因素造成的。其转子产生的干扰频率高于10 Hz[5],由于CMG的响应带宽有限,该高频振动将直接传递给星体。而目前的光学有效载荷对振动诱发的信号跳动或不稳定极其敏感,因而要求为它们提供极其稳定的平台。首先需要对振动源进行振动隔离,在对飞轮和CMG隔振方面,一些航天器上多采用被动隔振平台进行振动隔离,如JWST[2]、航天空间干涉仪任务(SIM)[6]、GONES-N航天器[7]、太阳动态观测任务(SDO)[8]、TPF-C[3]、Worldview I、Worldview II和Pleiades-HR卫星[9]。其次还需要在光学有效载荷和星体之间加装Stewart平台式隔振装置,如在STRV-2卫星和PICOSat卫星上分别对光学有效载荷的平台式隔振系统VISS (Vibration Isolation and Suspension System)[10-11]和SUITE (Satellite Ultra-quiet Isolation Technologies Experiment)系统进行了成功的搭载试验[12-13]。此外,隔振单元件的设计很好地提供了隔振系统应用的空间。值得一提的是Honeywell公司生产的D-strut系列隔振器,如D-strut,D-strutTM,1.5 Hz D-strut,Adaptable D-strutTM和Hybrid D-strut[14-18]等。这些隔振单元件在隔振系统的设计中应用广泛。
然而,目前对两级隔振系统的研究多集中在用有限元的方法建立系统级动力学模型。用该方法建立系统级动力学模型需要完全已知卫星结构,所建立的模型不具有普遍性,当星体增加或减少部件时,需重新进行有限元建模,并且该方法不利于分析所引入的隔振系统对星上其他系统的影响等。本文将针对两级隔振系统在星上的应用,利用牛顿欧拉法进行系统级动力学建模,并重点分析隔振平台参数变化给姿态控制系统带来的影响。通过限定参数范围,选择合理参数,分析两级隔振系统的频域特性,并通过频谱对比分析两级隔振系统对光学有效载荷姿态稳定度的改善程度,为中国高分辨率遥感卫星的研制提供理论支持。
1 整星动力学模型
本文研究的对象是如图1所示的某类型卫星,其中对光学有效载荷实施两级隔振,两级隔振系统在星上的安装形式如图2所示,首先使用一个隔振平台实现对多个CMG进行振动隔离,其次再在光学有效载荷和星体之间加装隔振平台。

图1 星体示意图Fig.1 Sketch map of the satellite

图2 带有隔振系统卫星的坐标系描述Fig.2 Reference frames of the satellite with the vibration isolation
将多个控制力矩陀螺称之为控制力矩陀螺群(CMGs),由于CMGs和隔振平台的上平台固连,故将CMGs和隔振平台的上平台称之为CMGs上平台系统;将光学有效载荷和其隔振平台的上平台称之为光学有效载荷上平台系统;将隔振平台的下平台和星体合称为下平台系统,即星本体系统。
定义惯性坐标系为fe;CMGs上平台系统的固连坐标系为fu;星体的固连坐标系为fb;光学有效载荷上平台系统的固连坐标系为fpu;光学有效载荷固连坐标系为fpl;CMGs隔振平台的下平台固连坐标系为fd;有效载荷隔振平台的下平台固连坐标系为fpd;第j个挠性帆板的体坐标系为ffj,为建立此类问题的通用动力学模型,假设卫星带有H个挠性帆板。定义Amn为从fn到fm的转换矩阵;rmn为从fn坐标系原点到fm坐标系原点的矢量。其中,fm和fn为任意坐标系。坐标系的设定可参见图2。
本文采用牛顿欧拉法建立整星动力学模型。首先分别建立CMGs上平台系统动力学模型和有效载荷上平台系统动力学模型;其次,由两个隔振平台的上平台运动带动隔振平台各个支杆的运动,推导得出各个支杆产生对上平台连接点和对下平台连接点的力;最后,根据力的相互作用原理,推导得出星本体系统的动力学方程。
工程中,挠性帆板通常不施加分布控制力;中心刚体角速度、挠性帆板相对中心体的角速度和挠性帆板弹性振动速度通常是小量,则由此引起的高阶非线性耦合项可忽略。经过以上假设,可分别得到CMGs上平台系统和光学有效载荷系统的动力学方程为
(1)
(2)
Fpi=csi(Aueωli-ωu)
(3)
Fplh=csh(Apleωlh-ωpl)
(4)
式中:上标“×”表示列阵的反对称斜方阵;mu和Iu分别为CMGs上平台系统的质量和惯量;mpl和Ipl分别为光学有效载荷的质量和惯量;Su和Spl分别为CMGs上平台系统和光学有效载荷的静矩;vu和ωu分别为CMGs上平台系统的速度和角速度;vpl和ωpl分别为光学有效载荷的速度和角速度;Fd和Td分别为由CMGs引起的扰动力和扰动力矩;Tc为CMGs产生的有效输出力矩;Fsi和Fpsh分别为球铰作用在各自上平台上的力;N和M分别为CMGs隔振平台和有效载荷隔振平台的支杆数;pi和pph为两个隔振平台的上平台质心到上平台连接点处的矢量列阵;Fpi和Fplh分别为由两个隔振平台的球铰引起的摩擦力矩;csi和csh分别为两个隔振平台球铰的摩擦系数;ωli和ωlh分别为两个隔振平台各支杆的角速度。
星本体系统的动力学方程为
(5)
Fqi=cui(Abeωli-ωb)
(6)
Fqlh=cuh(Abeωlh-ωb)
(7)

帆板的转动方程和振动方程分别为
(8)
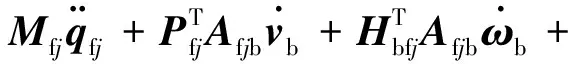
(9)
式中:Mfj为帆板的模态质量矩阵;Cfj和Kfj分别为帆板的阻尼矩阵和刚度矩阵;Tfj为帆板转动受到的力矩。为建模方便,本文所关注的CMG扰动主要是由转子静/动不平衡引起的。其他由于安装误差引起的扰动影响较小,可被忽略[19]。因此可得Fd和Td的具体表达式为
(10)

(11)
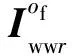
(12)

式(1)~式(12)共同组成了含有CMGs、光学有效载荷、太阳帆板以及两级隔振系统的整星动力学模型。
为验证所推导的含有两级隔振系统的整星动力学模型的正确性,通过使用ADAMS工程软件采用另一种建模方式建立系统模型,其中CMGs认为是锁死状态,假设卫星带有3个挠性太阳帆板。本文所采用的两个隔振平台均为正立方体Stewart隔振平台,隔振平台的支杆可被简化成弹簧阻尼并联的两参数模型,其中上平台和支杆的连接形式为球铰连接,下平台和支杆是万向节连接[20]。隔振平台的上下平台直径为1 m,每个支杆长为612.4 mm,平台高度为353.6 mm,支杆的刚度系数和阻尼系数分别为k=20 000 N/m,c=500 N·s/m[21]。
光学有效载荷的质量和惯量为
mpl=20 kg,Ipl=diag(1.45,1.45,2.8) kg·m2
星体的质量和惯量为
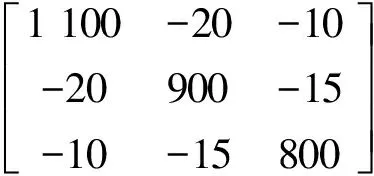
CMGs上平台系统的质量和惯量为
mp=82.8 kg,Ip=diag(8.8,8.8,15) kg·m2

图3 光学有效载荷位置响应的MATLAB仿真图Fig.3 Position response curves of the optical payload obtained by using MATLAB

图4 光学有效载荷位置响应的ADAMS仿真图Fig.4 Position response curves of the optical payload obtained by using ADAMS
2 频域特性分析
本节在合理性假设的前提下对所建立的含有两级隔振系统的整星动力学模型进行简化,分别求得从扰动源到星体和到光学有效载荷的传递函数矩阵,以重点分析CMGs隔振平台参数变化对姿态控制系统的影响,得到CMGs隔振平台参数设计的约束条件,并根据约束条件选择合理参数分析两级隔振系统的频域特性。
2.1 传递函数矩阵计算
对于小幅值振动分析,可假定运动中隔振平台的构型近似不变,速度为小量,二次以上速度量可忽略;并且在小角度假设情况下,有效载荷固连坐标系、CMGs上平台系统固连坐标系以及星体固连坐标系到惯性坐标系的转换矩阵可认为是单位阵;由于各隔振平台支杆的质量和惯量对各个通道的传递函数影响较小,在分析过程中也可忽略。此外,由于航天器的附件常常工作在锁定状态,或采用步进电机进行控制,则附件相对于中心体的角速度为零。
基于以上基本假设,可将式(1)、式(2)、式(5)、式(8)和式(9)简化为
(13)
(14)
(15)
(16)
式中:t、tpl和b分别为惯性坐标系中心到CMGs上平台系统质心、有效载荷质心和星体质心的位置矢量列阵;θu、θpl和θb分别为CMGs上平台系统、有效载荷和星体的转动角度。假设卫星共有3块太阳帆板,因此,j=1,2,3。
Fsi和Fpsh的表达式可以简化为
(17)
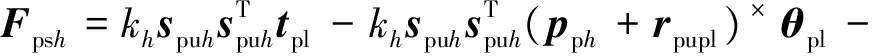
(18)
式中:ki和ci分别为CMGs隔振平台的刚度系数和阻尼系数;kh和ch分别为有效载荷隔振平台的刚度系数和阻尼系数;sui和spuh分别为两个隔振平台支杆方向的单位矢量。
令
(19)

(20)

(21)
则Fsi和Fpsh的表达式可以改写为
(22)
(23)
整星系统的动力学方程可以写为
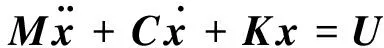
(24)
式中:
M=diag(M1,M2,M3)




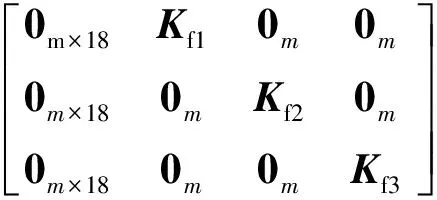
式中:E为单位矩阵。
定义星体所受到的广义力为输出量,则可将其表示为
(25)
式中:

{

Y=CzX+Du
(26)
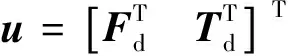
(27)

为能考察不同频率下的扰动力和扰动力矩对有效载荷的影响,可将有效载荷的位移、角度、速度和角速度作为输出量,则只需将式(26)中Cz的表达进行一定的变化即可得出此时的状态方程。此时
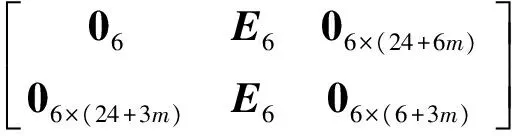
(28)
此时的D=012×6。由G(s)=Cz(sE-A)-1·B+D可以求得系统传递函数矩阵。传递函数矩阵G(s)可根据选择不同隔振平台参数以及有效载荷和卫星质量特性参数计算得出。
2.2 CMGs隔振平台参数分析
本文所选用的两级隔振平台均是被动机械结构,可保证在轨运行期间安全可靠。但是,在实际加工过程中,隔振平台某些重要参数和要求值不能完全对应,加之在轨过程中会存在更多的参数不确定因素。因此,需要分析隔振系统的重要参数在变化情况下对系统带来的影响。
被动隔振系统最重要的性能参数是各个方向上的隔振频率以及隔振频率处的放大倍数,主要是由隔振平台单元件的刚度系数和阻尼系数决定[22]。对于光学有效载荷隔振平台,它只起到隔振的作用,因此可以不作参数变化影响分析。而安装在CMGs和星体之间的隔振平台不仅起着隔振的作用,还要传递有效的力矩以实现姿态控制。因此该隔振系统的引入是否会影响PID姿态控制系统的正常工作需要详细讨论。
以PID控制器作为姿态控制器,PID控制器可写为

(29)
式中:τp和τq为已知参数;K为PID控制器增益。
在分析CMGs隔振平台对PID姿态控制系统的影响中,暂时忽略挠性帆板的影响以及执行机构的动态特性,并认为星体解耦,对每个控制通道进行单独分析。其中控制系统框图如图5所示。
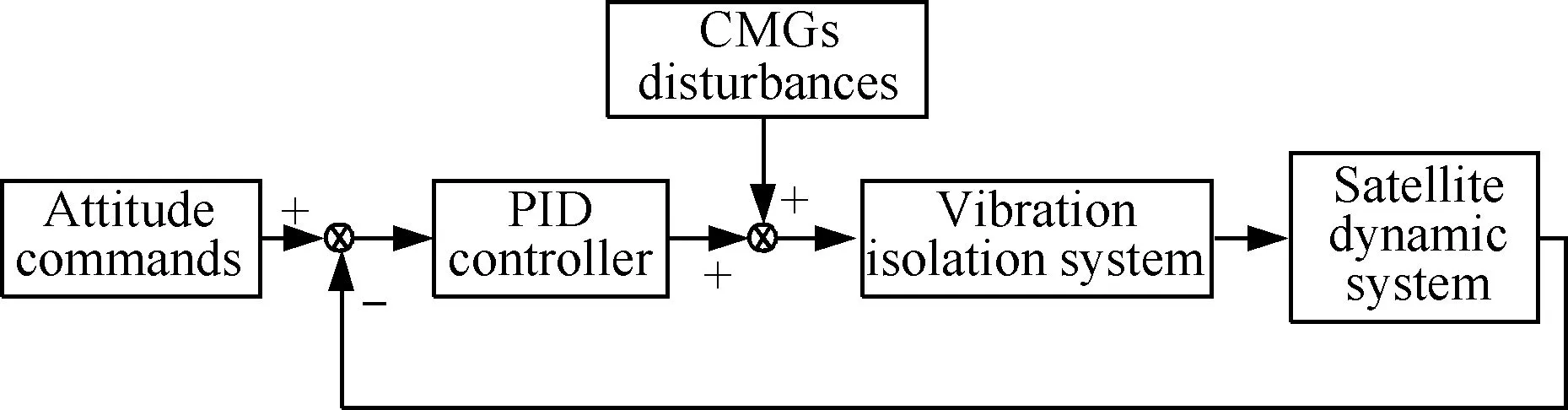
图5 控制系统框图Fig.5 Block diagram of the control system
结合CMGs隔振平台上平台系统以及星体的质量惯量特性,根据2.1节所推导的从扰动源到星体的传递函数矩阵,可写出每个控制通道下的CMGs隔振平台的传递函数为

(30)

(31)
GYaw(s)=(cis+ki)/(20s2+cis+ki)
(32)

(33)
结合系统控制框图图5可得知每个控制通道的开环传递函数,由于每个控制通道的分析方式类似,本文仅以x轴转动通道进行分析。x轴转动通道的开环传递函数如式(33)所示。初始参数设置如下:
τp=0.079,τq=5×10-4,Ix=1 100 kg·m2,ci=500 N·s/m,ki=20 000 N/m
结合式(33)可以绘制得出滚动通道下含有隔振平台传递函数后的开环系统根轨迹图,如图6所示。

图6 x轴转动通道下的开环系统根轨迹图Fig.6 Root locus diagram in x-rotation direction
由图6可知,加隔振平台传递函数后,相当于在原有的系统中引入了3个零点4个极点(图中标有0的是引入的零点,标有1的是引入的极点)。其中有两个共轭极点随着PID控制器增益K值的增大会走向复平面的右半平面,导致系统失稳。因此,引入隔振平台传递函数后,系统条件稳定,需要对PID控制器参数进行范围限定。可以通过根轨迹图确定系统稳定的增益范围。在这个范围中,选择系统稳定的控制参数,分别绘制系统的Bode图和Nyquist图,得到系统的稳定裕度,选择最佳的控制参数。
对于滚动通道,系统稳定的K值的范围大致为
0.04 (34) 一般情况下,当航天器任务确定以后,各通道下的姿态控制系统带宽就会确定,也就意味着PID控制器参数已经确定。在PID控制器参数固定的情况下,令CMGs隔振平台参数可变,可以进一步分析隔振平台隔振频率和姿态控制系统带宽之间的关系,为隔振平台参数设计提供有效的约束条件。 令Kp=2 000,Ki=0.1,Kd=3 200,则可得出各主通道的控制系统带宽约为0.5 Hz。假设CMGs隔振平台的刚度系数和阻尼系数是变化的,则可得到不同的隔振频率和隔振频率处的放大倍数。以该隔振平台的x轴转动方向为例,绘制不同放大倍数情况下,控制系统带宽倍数的隔振频率同开环控制系统的稳定裕度关系图,如图7所示,图中n为共振幅值。 图7 x轴转动通道下的隔振频率同开环控制系统稳定裕度的关系图Fig.7 Relationship between the corner frequency and the amplitude margin of the open-loop system in x-rotation direction 工程上隔振系统的放大倍数为3~6倍都是合理的。为能实现姿态控制系统的充分稳定,一般选择幅值裕度为6~20 dB。因此由图7可知,只有当x轴转动通道下的隔振平台隔振频率是控制系统带宽的10倍以上时,闭环控制系统才能保证充分稳定。其他通道下的情况和此一样,这里不再赘述。 因此,当使用了CMGs隔振平台后,为了能够充分保证姿态控制系统的稳定性要求,则需要重新设定PID控制器参数,或者使得CMGs隔振平台的各主通道隔振频率达到控制系统带宽的10倍以上,为工程实现和在轨参数变化留有余量。 2.3 频域仿真分析 结合以上对CMGs隔振平台参数约束的分析,以及2.1节的传递函数矩阵表达式计算流程,可合理选择相关参数,进行两级隔振系统的频域分析。 光学有效载荷隔振平台的刚度系数和阻尼系数选择为kh=20 000 N/m,ch=300 N·s/m。隔振频率分布为5.17~9.34 Hz。帆板的阻尼系数为0.7%;帆板的前3阶模态选择如下: 为能充分满足控制系统稳定性要求,CMGs隔振平台的隔振频率选择在系统带宽10倍以上,放大倍数选择为4倍,则各支杆刚度系数和阻尼系数为ki=150 000 N/m,ci=800 N·s/m,此时各个主通道的隔振频率分布为6.83~11.5 Hz。z轴转动通道的隔振频率最大,为11.5 Hz。由于CMGs隔振平台不仅要对CMGs扰动进行振动隔离,还要传递有效的输出力矩以实现姿态控制。因此,对于隔振频率较大的z轴转动通道需要重点分析挠性帆板是否影响正常的力矩输出能力。结合以上参数,并运用式(26)和式(27),可绘制z轴转动通道下的力矩传递率曲线,如图8所示。 由图8可知,光学有效载荷隔振平台和太阳帆板对低于2 Hz的输出力矩均无影响,并且z轴转动通道的隔振频率仍在11.5 Hz附近,未受到影响。故可得知所选择的光学有效载荷两级隔振平台参数是合理的,并可用于下面进一步的分析。 图8 z轴转动通道下的力矩传递率曲线Fig.8 Transmissibility curve of torque in z-rotation direction 同样结合式(26)和式(28),可绘制从扰动源到光学有效载荷姿态角速度的传递率曲线,如图9所示。图9仅给出了x轴转动通道下的传递率曲线,其他通道的传递率曲线类似。 图9 x轴转动通道下的扰动到有效载荷姿态角速度的传递率曲线Fig.9 Transmissibility curve from CMGs disturbance to attitude angular velocity of optical payload in x-rotation direction 由图9可知,当扰动频率高于11 Hz的时候,光学有效载荷的姿态稳定度和不加隔振系统相比有明显的提高;而在6.8~11 Hz之间和不加隔振系统相比较,有放大效果,主要是由于扰动和CMGs隔振平台的隔振频率同频产生共振引起的。因此,可将CMGs转子转速尽量安排在100 Hz附近(转子静动不平衡产生的扰动和转子转速同频),以发挥隔振系统的优势。 针对第1节所建立的整星动力学模型进行时域仿真,以验证两级隔振系统能够在星上得到良好的应用。 CMG的静动不平衡量分别为13.6 g·cm和17 g·cm2。姿态角度初始值1.5°,完成姿态稳定控制。姿态角速度测量噪声为10-6rad/s(1σ);姿态角速度测量带宽可达500 Hz;姿态角度测量噪声为10″(1σ);CMG框架角速度测量误差为10-3(°)/s(1σ);控制力矩陀螺标称角动量是20 N·m·s;最大框架角速度是0.25 rad/s,最小框架角速度是0.05 rad/s。 为进一步验证选用参数的合理性,需首先由频域方法得出控制系统各主要通道的稳定裕度和带宽,如表1所示。 表1各通道下的稳定裕度和带宽 Table1Stabilitymarginsandbandwidthforeachrotationdirection DirectionAmplitudemargin/dBPhasemargin/(°)Bandwidth/Hzx⁃rotation167550463y⁃rotation142770513z⁃rotation2377350523 由表1可知,所选择的两级隔振平台参数能满足系统稳定性的要求。为进一步验证两级隔振系统参数的合理性以及两级隔振系统对光学有效载荷姿态稳定度的改善程度,分别进行了以下的时域仿真和幅频特性对比仿真。 对光学有效载荷姿态角速度进行频谱分析,如图13所示。在CMG转子转速频率处光学有效载荷姿态角速度具有振动特性,这种振动主要是由CMG扰动所致,该扰动是由CMG转子静动不平衡引起的,并且扰动频率和转子转速同频。 图10 光学有效载荷的姿态角随时间变化曲线Fig.10 Curves of attitude angles of the optical payload vs time 图11 光学有效载荷的姿态角速度随时间变化曲线Fig.11 Curves of attitude angular velocities of the optical payload vs time 图12 CMGs的框架角度随时间变化曲线Fig.12 Curves of gimbal angles of the CMGs vs time 分别选择CMG转子转速为100、120、140、160、180、200 Hz,对不含有任何隔振系统、仅含有CMGs隔振平台和含有两级隔振系统的光学有效载荷姿态角速度分别进行时域仿真,对仿真数据进行频谱分析,如图14所示。当星上使用了两级 图13 在x轴转动通道下光学有效载荷姿态角速度频谱图Fig.13 Spectrogram of attitude angular velocity of the optical payload in x-rotation direction 图14 光学有效载荷姿态角速度抖动幅值对比图Fig.14 Contrast of vibration amplitude spectrum of the attitude angular velocity of the optical payload 隔振系统后,光学有效载荷的姿态角速度在CMG转子转速频率处的振动幅值能够得到大幅度的衰减,和不使用隔振系统的情况相比,衰减了近两个量级,极大地衰减了高频振动,这将提高光学有效载荷的稳定度,进一步提高光学有效载荷的成像质量。 采用两级隔振的方式,为光学有效载荷提供超静环境。重点建立了含有两级隔振系统以及光学有效载荷、CMGs和挠性太阳帆板的整星动力学模型,并验证了模型的正确性。该模型具有普遍性和推广性,即如果星上其他部件还需使用杆状支撑结构作为隔振系统进行振动隔离,只需在整星动力学模型中再加入某一部件隔振平台上平台系统的动力学模型,并将支杆的作用力和作用力矩表达式加在星本体系统的动力模型中即可实现含有多级隔振系统的整星动力学建模。相比有限元方法,本文的建模方法具有便捷性和较强的数值仿真性。 此外,推导出了从扰动源到星体和到光学有效载荷的传递函数矩阵,并重点分析了CMGs隔振平台对姿态控制系统的影响。得知当使用了CMGs隔振平台后,卫星姿态控制系统将条件稳定,必须重新限定PID姿态控制系统参数,或者在CMGs隔振平台设计时将各通道隔振频率约束在系统控制带宽的10倍以上,方能满足姿态控制系统的充分稳定。 本文重点针对传递给光学有效载荷的高频扰动进行振动隔离研究,提出一种两级被动隔振方案,并验证了其有效性。但是对于星上还存在一些低频扰动,这些扰动同样影响着光学有效载荷的成像精度,因此针对星上低频扰动,进行主动振动控制技术研究或者通过使用快速控制反射镜以减小光束抖动成为了进一步研究的方向。 [1] Davis L P, Wilson J F, Jewell R E. Hubble space telescope reaction wheel assembly vibration isolation system, structural dynamics and control interaction of flexible structures. NASA Report N87-22702, 1986: 669-690. [2] Bronowicki A J. Vibration isolator for large space telescopes. Journal of Spacecraft and Rocket, 2006, 43(1): 45-53. [3] Blaurock C, Liu A, Dewell L, et al. Passive isolator design for jitter reduction in the terrestrial planet finder coronagraph. Optical Modeling and Performance Precisions II. San Diego: SPIE, 2005: 1-12. [4] Pang S W, Yang L, Qu G J. New development of micro-vibration integrated modeling and assessment technology for high performance spacecraft. Structure & Environment Engineering, 2007, 34(6): 1-9. (in Chinese) 庞世伟, 杨雷, 曲广吉. 高精度航天器微振动建模与评估技术最近进展. 强度与环境, 2007, 34(6): 1-9. [5] Zhao Y, Sun J, Tian H. Development of empirical and analytical reaction wheel disturbance models. Aircraft Engineering and Aerospace Technology, 2006, 78(4): 326-330. [6] Wang X. The mask design for space interferometer mission (SIM). Optical and Infrared Interferometry. France: SPIE, 2008. [7] Miller S E, Kirchman P, Sudey J. Reaction wheel operational impacts on the GOES-N jitter environment. AIAA-2007-6736, 2007. [8] Liu K C, Maghami P. Reaction wheel disturbance modeling, jitter analysis, and validation tests for solar dynamics observatory. AIAA-2008-7232, 2008. [9] Baudoin A, Boussarie E, Damilano P, et al. Pleiades: a multi mission and multi cooperative program. Acta Astronautica, 2002, 51(1-9): 317-327. [10] Stubstad J M, Shoemaker J R, Brooks P. Space technology research vehicle (STRV)-2 program. Small Payloads in Space. San Diego, USA: Society of Photo-Optical Instrumentation Engineers, 2000: 36-47. [11] Cobb R G, Sullivan J M, Das A, et al. Vibration isolation and suppression system for precision payloads in space. Smart Material and Structure, 1999, 8(6): 798-812. [12] Anderson E H, Fumo J P, Erwin R S. Satellite ultraquiet isolation technologies experiment (SUITE). 2000 IEEE Aerospace Conference. Big Sky, MT: Institute of Electrical Engineers Computer Society, 2000: 199-313. [13] Babuska V, Erwin R S, Sullivan L A. System identification of the SUITE isolation platform: comparison of ground and flight experiments. AIAA-2003-1642, 2003. [14] Anderson E, Trubert M, Fanson J, et al. Testing and application of a viscous passive damper for use in precision truss structures. AIAA-1991-996, 1991. [15] Davis L P, Workman B J. Design of a D-strut and its application results in the JPL, MIT, and LaRC test beds. AIAA-1992-2274, 1992. [16] Davis L P, Cunningham D, Harrell J. Advanced 1.5 Hz passive viscous isolation system. AIAA-1994-1651, 1994. [17] Davis L P, Cunningham D, Bicos A, et al. Adaptable passive viscous damper (an adaptable D-strutTM). Smart Structures and Materials 1994: Passive Damping. Orlando, FL: SPIE, 1994: 47-58. [18] Davis L P, Carter D R, Hyde T T. Second generation hybrid D-strut. Smart Structures and Materials 1995: Passive Damping. San Diego, CA: SPIE, 1995: 161-175. [19] Jin L. Study on attitude dynamics and control of spacecraft using angular momentum exchange devices. Beijing: School of Astronautics, Beihang University, 2008. (in Chinese) 金磊. 使用角动量交换装置的航天器姿态动力学与控制问题研究. 北京: 北京航空航天大学宇航学院, 2008. [20] Mahboubkhah M, Nategh M J, Khadem S E. A comprehensive study on the free vibration of machine tools’ hexapod table. The International Journal of Advanced Manufacturing Technology, 2009, 40(11-12): 1239-1251. [21] Zhang Y, Xu S J. High frequency vibration isolation of CMG for satellite. Journal of Astronautics, 2011, 32(8): 1722-1727. (in Chinese) 张尧, 徐世杰. 星上控制力矩陀螺的高频抖动减振研究. 宇航学报, 2011, 32(8): 1722-1727. [22] Oh C S, Lee W, Bang H. Passive jitter isolation for reaction wheel of satellites. SICE-ICASE International Joint Conference. Bexco: Institute of Electrical Engineers Computer Society, 2006: 3891-3895. Dual-stageVibrationIsolationofOpticalPayloadsforSatellites ZHANGYao,XUShijie* SchoolofAstronautics,BeihangUniversity,Beijing100191,China Inordertorealizehighqualityimagingperformancefortheopticalpayloadofasatellite,adual-stagepassivevibrationisolationsystemisdiscussedinthispaper.Thefirststageofvibrationisolationisattheactuatordisturbancesourcelikethecontrolmomentgyros(CMGs).Thesecondstageofisolationisplacedbetweenthetopofthesatellitebusandtheopticalpayload.Firstly,anintegratedsatellitedynamicmodelisbuilt,includingadual-stagevibrationisolationsystem,pyramidconfigurationCMGsandsolararrays,andthevalidityofthisdynamicmodelisverifiedbyADAMS.Secondly,thesatellitesystemleveldynamicmodelissimplifiedbasedonreasonableassumptions.ThetransferfunctionmatricesfromCMGsmotiontosatellitemotionandthattoopticalpayloadmotionarederived.TheinfluenceofthevibrationisolationplatformofCMGsontheattitudecontrolsystemisanalyzed.Thenthefrequencydomaincharacteristicsofthisvibrationisolationsystemarediscussedintermsoftherationallyselectedparametersofthedual-stagepassivevibrationisolationsystem.Finally,therationalityoftheparametersofthedual-stagevibrationisolationsystemandthefeasibilityofitsapplicationareprovedbynumericalsimulation.Thesimulationresultsillustratetheameliorativeeffectofthedual-stagevibrationisolationsystemontheattitudestabilizationoftheopticalpayloadatthefrequencyoftherotorspeed. imagequality;opticalpayload;jitter;dynamics;vibrationisolation 2011-12-09;Revised2012-01-05;Accepted2012-02-27;Publishedonline2012-03-201100 URL:www.cnki.net/kcms/detail/11.1929.V.20120320.1100.006.html NationalNaturalScienceFoundationofChina(10902003) .Tel.:010-82339275E-mailstarsjxu@yahoo.com.cn 2011-12-09;退修日期2012-01-05;录用日期2012-02-27; < class="emphasis_bold">网络出版时间 时间:2012-03-201100 www.cnki.net/kcms/detail/11.1929.V.20120320.1100.006.html 国家自然科学基金(10902003) .Tel.:010-82339275E-mailstarsjxu@yahoo.com.cn ZhangY,XuSJ.Dual-stagevibrationisolationofopticalpayloadsforsatellites.ActaAeronauticaetAstronauticaSinica,2012,33(9):1643-1654. 张尧,徐世杰.星上光学有效载荷的两级隔振研究.航空学报,2012,33(9):1643-1654. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 1000-6893(2012)09-1643-12 V412.4 A 张尧男, 博士研究生。主要研究方向: 航天器动力学与控制。 Tel: 010-82339751 E-mail: zhangyao7000@yahoo.cn 徐世杰男, 博士, 教授, 博士生导师。主要研究方向: 空间飞行器姿态动力学与控制, 鲁棒控制和非线性控制等。 Tel: 010-82339275 E-mail: starsjxu@yahoo.com.cn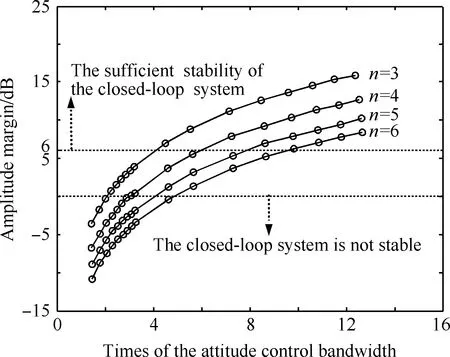


3 整星的数值仿真







4 结 论

