含胶层复合材料梁构件性能分析
王东方, 杨嘉陵
北京航空航天大学 航空科学与工程学院, 100191 北京
含胶层复合材料梁构件性能分析
王东方, 杨嘉陵*
北京航空航天大学 航空科学与工程学院, 100191 北京
复合材料剪切模量通常比弹性模量低1个数量级,这就导致复合材料梁结构剪切效应比普通梁结构显著得多,尤其是梁截面高度较大的情况。作为夹胶玻璃等结构的复合材料支撑框架,复合材料方管梁翼缘通常存在较弱的胶层,此时复合材料梁横截面包含不同剪切模量的材料层,这就导致梁横截面在剪切作用下发生复杂的翘曲。剪切翘曲效应对梁结构的性能有着极大的影响,本文在分段线性位移场假设基础上,推导了对称面内变形的方管梁结构静力以及自振周期计算模型,并同经典梁理论计算结果进行对比,分析了梁几何参数、胶层力学参数等因素对两个模型计算误差的影响。计算结果表明,当胶层较弱时,弱层带来的层间剪切效应对梁的性能有着决定性的影响,此时经典梁理论不再适用。
方管梁; 复合材料; 横截面翘曲; 胶层; 分段线性
近年来,在航空工程中,复合材料层合板得到了广泛的应用,许多飞机内部都有相当一部分的复合材料承载框架。当前针对复合材料层合板的研究大多集中在复合材料板壳[1-7]上,而针对复合材料梁构件的研究数量[8-15]相对较少,已有的研究基本上集中在薄壁梁构件以及含分层复合材料梁构件[16-18]上,其理论一般都建立在一阶剪切基础上。关于厚壁梁的研究目前还很少见,Kim和White[19-20]采用Reddy建立的整体三次位移场理论[3]建立了闭合厚壁复合材料梁的计算模型。
复合材料框架构件多为方管式梁,为提高梁构件的承载力,通常在梁的上、下表面附加几片成型复合材料板,此时方管梁翼缘厚度增加,方管梁可能成为厚壁梁。另外在某些型号飞机座舱复合材料结构中,采用复合材料制作的夹胶玻璃边框架,翼缘存在多层胶层、多层玻璃以及复合材料板。通常来说,复合材料的剪切模量远低于面内弹性模量,因此同普通梁构件相比,复合材料梁构件的剪切效应对其性能有着更加显著的影响。而且对于含胶层复合材料层合梁来说,一般情况下胶层的力学性能远弱于复合材料。在这种情况下,梁构件横截面将很难满足平截面假设,此时采用经典梁理论进行求解将不可避免地带来一定的误差。当前复合材料梁的研究基本上是基于整体位移场进行计算的,然而当梁横断面上各部分剪切模量相差较大且翼缘承担剪力不可忽略时,复合材料梁横断面在剪力作用下的翘曲很难用简单的整体位移场进行描述,此时将不得不采用分层位移场[21]进行计算。目前关于有弱层的复合材料梁的研究还很少见,为分析胶层以及剪切效应对复合材料梁构件性能带来的影响,本文假定沿着梁截面高度位移场为分段线性,推导了含胶层复合材料方管梁构件的静力计算模型与自振频率计算模型,并同经典梁理论计算结果相对比,分析了两个模型之间计算误差的影响因素。
1 复合材料层合梁静力计算模型
图1所示复合材料梁为典型的含弱层层合梁构件,假定图1所示复合材料层合梁在对称面内弯曲,通常每一片复合材料层合板由几十层复合材料铺成(如图2所示),如果计算时细化到每一层都假定为位移分段线性,计算量将很庞大,而且也不太必要。由于单片层合板各层剪切模量相差不大且厚度较薄,因此在计算时位移场可假定如下:
1) 上翼缘附加单片层合板沿着厚度方向位移线性分布。
2) 上翼缘胶层沿着厚度方向位移线性分布。
3) 复合材料方管上翼缘位移沿着厚度方向线性分布。
4) 复合材料腹板因截面高度大,剪应力相对较高,为减小误差,沿着截面高度分为4段,每一段位移沿着截面高度方向线性分布。
5) 下翼缘各层位移场假定同上翼缘。
6) 如果翼缘有多个弱胶层,则应在每个弱胶层界面进行分段,假设整个梁断面共划分为m段,则加上上下表面共有m+1个界面。
7) 假设层合梁在对称面内变形,不考虑z向位移。

图1 层合梁横截面Fig.1 Cross section of a laminate beam

图2 单片层合板铺层示意图Fig.2 Layer diagram of a single laminate plate
1.1 平衡控制方程的推导

在位移沿厚度方向线性分布的假设下,单片层合板第i层位移场可以表示为
(1)
另外由于位移场沿厚度方向线性分布,u1i、w1i、u2i、w2i与层合板上下表面位移u1(x)、w1(x)、u2(x)、w2(x)应该满足
(2)
式中:yi为第i个界面的y轴坐标;h为单片层合板厚度。
第i层应变的表达式为
(3)
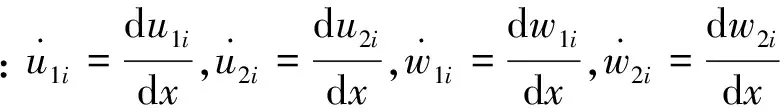
一般性各向异性材料本构方程为

(4)
式中:c1~c6为复合材料力学参数。
将式(3)和式(4)代入第i层结构势能表达式,可得

(5)
式中:B为层合板宽度;

单片层合板各层势能组装在一起,其结构势能表达为
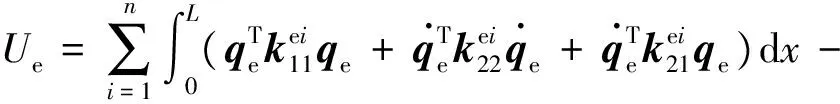
(6)

式(6)为单片层合板线性位移假设下结构势能的表达式。如图1所示复合材料梁,根据前述位移假设,可分别建立胶片层等各段结构势能表达式,然后仿照有限元结构刚度矩阵的建立方法,将各层结构刚度矩阵组装在一起,形成整体层合梁结构的势能表达式。其中在形成腹板结构势能表达式时,复合材料层合板材料参数同翼缘不同,腹板应采用复合材料面内材料参数,而翼缘则应采用面外材料参数。根据第1节的位移假设6),沿着高度方向将腹板共分为m段,则加上上下表面后,共有界面数为m+1,结构势能表达式为
(7)
式中:q=[u1w1u2w2…umwm

基于最小势能原理,对层合梁结构势能式(7)进行变分,并假设梁两端固定,即δq=0(x=0,x=L),可得
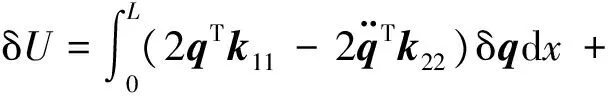
(8)
从而可得到结构的静力平衡控制方程为
(9)
1.2 边界条件的引入
假设层合梁两端边界条件为
ui(0)=0,wi(0)=0,ui(L)=0,wi(L)=0
(i=1,2,…,m+1)
可以假定位移具有下列形式:
(10)
式(10)满足层合梁两端的边界条件,代入式(9),可得
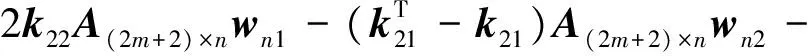
(11)
式中:
由迦辽金法[22],式(11)两端分别乘以sin(iπx/L) (i=1,2,…,n),并在[0,L]区间积分,整理之后可得
K(2m+2)n×(2m+2)nA(2m+2)n×1=cp(2m+2)n×1
(12)
求解式(12),可求得A(2m+2)n×1,即a1n、a2n、a3n、a4n、…、a(2m+1)n、a(2m+2)n,代入式(10),即可求得层合梁各点位移。
2 复合材料层合梁自振频率计算模型
式(5)中计入惯性力-ρu,tt的影响,可得

(13)
对层合梁各层组装后,结构势能表达式为
(14)
对式(14)进行变分,可得
(15)
假设q,tt=-ω2q,其中ω为结构自振频率,代入式(15)可得
(16)
假设层合梁结构两边固定,以类似于静力计算式(10)~式(12)的方法,可得
K(2m+2)n×(2m+2)nA(2m+2)n×1=
-ω2Km(2m+2)n×(2m+2)nA(2m+2)n×1
(17)
式(17)的求解是一个广义特征值问题,求解其特征值,即可得到结构的自振频率。
3 考虑横截面剪切翘曲效应计算结果同经典梁理论计算结果的对比分析
基于式(12)与式(17)进行求解,可得到考虑横截面剪切翘曲效应时层合梁结构静力荷载作用下的位移响应以及结构的自振频率。本文针对图3和图4所示的层合梁(两端固定)进行计算。
图3 计算结构简图Fig.3 Structural calculation diagram

图4 层合梁横断面Fig.4 Cross section of the beam
3.1 本文算法与有限元计算结果比较验证
首先为验证本文计算模型的合理性,分别采用本文算法以及Nastran通用有限元计算软件对含胶层层合梁进行计算分析。在有限元计算模拟过程中,为保证分析的精确性,采用三维单元划分有限元网格,三维有限元网格如图5所示。

图5 梁横断面及单元局部放大图Fig.5 Cross section and partial enlargement of the element of beam
计算中假设胶层、翼缘其他层以及腹板等材料为各向同性材料。胶层的力学参数假设为:泊松比为0.3,弹性模量为5 000 MPa,胶层厚度为2 mm。翼缘其他层以及腹板材料的力学参数假设为:泊松比为0.2,弹性模量为60 000 MPa,各层厚度相等,为2.1 mm。腹板高度hw=30 mm。在以上参数基础上分别采用本文建立的算法(Analytical Model)以及有限元模型(FE Model)对层合梁进行计算得到梁挠度曲线如图6所示。

图6 本文模型以及有限元模型计算得到的梁挠度曲线比较Fig.6 Comparison of deflection curves of beam based on model presented in this paper and FE model
由于有限元模型采用精细的三维单元进行计算,因此有限元计算结果充分考虑了层合梁的腹板剪切以及弱胶层的层间剪切影响。从图6可以看出,本文模型计算得到的梁挠度曲线同有限元模型计算得到的梁挠度曲线基本重合,这验证了考虑剪切翘曲效应的本文模型的正确性,因此本文模型的计算结果是可靠的。
3.2 弱胶层层间剪切影响因素分析
假设层合梁各部分的层合板为相同材料、相同铺层,翼缘与腹板位置层合板剪切模量不同。层合梁上层顶部作用着均布荷载p=10 kN/m,其余表面荷载为0,在此工况下分别采用本文提出的考虑横截面剪切翘曲效应的算法和经典梁理论计算结构静力荷载作用下的位移响应和结构的自振频率,探讨胶层力学参数、截面几何参数等因素对结构响应的影响。
3.2.1 胶层较强时横截面翘曲对结构响应的影响
计算中假设翼缘以及腹板层合板采用相同铺层[0°/90°/0°/90°/0°/90°/0°],每层厚度均为0.3 mm。假设翼缘层合板材料属性在0°方向为
腹板层合板材料属性在0°方向为
胶层材料属性:胶层泊松比为0.3,弹性模量E=5 600 MPa。在这种假设下,胶层剪切模量同复合材料剪切模量相当,从而在排除胶层影响的情况下分析是否考虑横截面剪切翘曲效应两个模型之间的差别。经典梁理论定义为模型1,考虑横截面剪切翘曲效应定义为模型2。分别采用两个模型编程计算,得到层合梁跨中位移以及层合梁的第1自振周期,如图7和图8所示。图7和图8的横坐标是腹板高度;图7的纵坐标是两个模型跨中中点位移相对误差((模型2-模型1)/模型1),图8的纵坐标是两个模型的第1自振周期相对误差((模型2-模型1)/模型1)。

图7 两种计算模型跨中位移对比图(E=5 600 MPa)Fig.7 Comparison of the midpoint displacement based on the two models (E=5 600 MPa)

图8 两种计算模型第1自振周期对比图(E=5 600 MPa)Fig.8 Comparison of the first vibration cycle based on the two models (E=5 600 MPa)
由图7和图8可以看出,随着腹板高度的增加,两个模型的计算误差也随之增大。由于在计算中,采取的胶层剪切模量同复合材料剪切模量相当,因此基本可以排除弱胶层对计算结果的影响。两个模型误差随腹板高度增大的主要原因在于,当腹板高度增加时,横截面剪切翘曲增大,因而采用经典梁理论计算误差会随之增大。
3.2.2 胶层较弱时横截面翘曲对结构响应的影响
假设复合材料层合板材料属性以及铺层顺序不变,胶层泊松比为0.3,弹性模量E=20 MPa,这种材料假设是很典型的含弱胶层层合梁。假设腹板高度在0~60 mm之间变化,计算得到层合梁跨中位移以及层合梁的第1自振周期如图9和图10所示。

图9 两种计算模型跨中位移对比图(E=20 MPa)Fig.9 Comparison of the midpoint displacement based on the two models (E=20 MPa)

图10 两种计算模型第1自振周期对比图(E=20 MPa)Fig.10 Comparison of the first vibration cycle based on the two models (E=20 MPa)
由图9和图10可以看出,随着腹板高度的增加,两种计算模型的误差逐渐减少,同图7和图8的变化趋势相反。其主要原因在于当胶层较弱时,胶层的层间剪切效应影响显著。当腹板高度较小时,翼缘承担的剪力相对较大,胶层的层间剪切效应也相对较大。此时横截面剪切翘曲效应主要体现在翼缘胶层界面的层间剪切上。由图9和图10的计算结果可以看出,当翼缘存在弱层(如胶层)时,经典梁理论的计算结果误差很大,此时应当采取分层位移场的方法进行计算。
3.2.3 胶层弹性模量对结构响应的影响
假设复合材料层合板材料属性以及铺层顺序不变,腹板高度固定为15 mm,胶层泊松比固定为0.3,其弹性模量在10~5 000 MPa之间变化,计算得到层合梁跨中位移以及层合梁的第1自振周期如图11和图12所示。

图11 两种计算模型跨中位移对比图(hw=15 mm)Fig.11 Comparison of the midpoint displacement based on the two models (hw=15 mm)
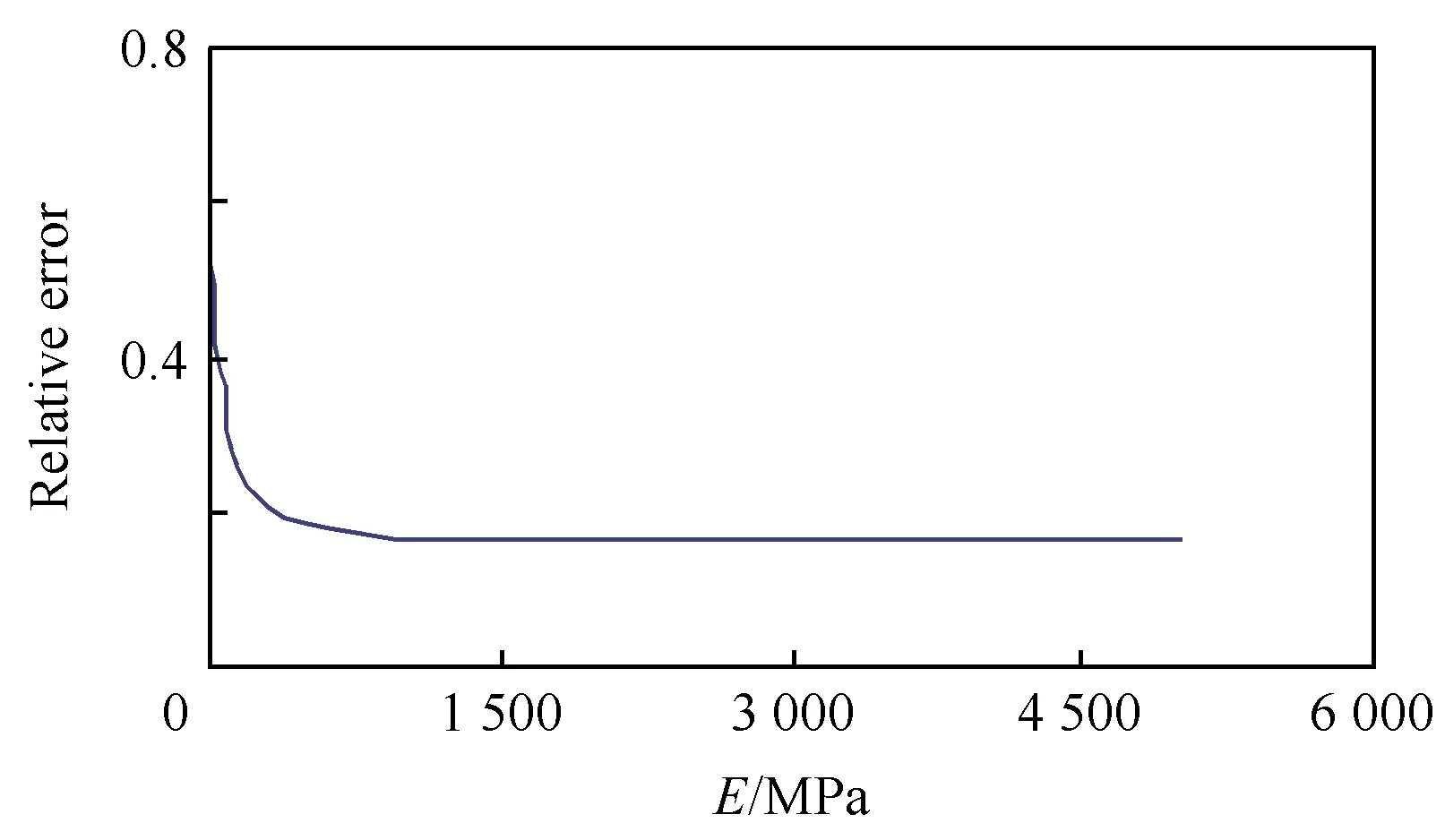
图12 两种计算模型第1自振周期对比图(hw=15 mm)Fig.12 Comparison of the first vibration cycle based on the two models (hw=15 mm)
由图11和图12的计算结果可以看出,在胶层弹性模量低于1 000 MPa时,两个模型的计算误差对胶层弹性模量的取值非常敏感,其主要原因在于:当胶层较弱时,胶层的层间剪切效应显著;而随着胶层性能增强,胶层的层间剪切效应逐渐减小,两个模型的计算误差也随之减小。
4 结 论
当层合梁翼缘存在胶层等弱层时,层合梁结构几何参数、胶层力学参数等对层合梁性能有显著的影响:
1) 当翼缘胶层较强,胶层界面层间剪切效应不显著时,经典梁理论计算误差相对较小,但计算误差会随着截面高度的增加逐渐增大。由于复合材料剪切模量通常比弹性模量低20~30倍,因此复合材料梁的剪切效应比普通梁大得多。因此当截面高度较大时,仅仅考虑一阶剪切效应的经典梁理论计算误差较大,此时应考虑层合梁的高阶剪切效应对结构响应的影响。
2) 当翼缘胶层较弱,胶层界面层间剪切效应显著时,不应采用经典梁理论进行计算,而应在分层位移场假设基础上进行计算。
3) 随着翼缘胶层弹性模量的增加,胶层界面层间剪切效应逐渐减小。当胶层是为了粘结复合材料层合板增加层合梁刚度时,应尽可能采用高弹性模量胶层;当复合材料梁是作为夹胶玻璃等支撑框架时,夹胶玻璃中的弱胶层、玻璃与梁之间的弱胶层对复合材料梁的性能影响较大,应采用分层位移场假设进行计算。
[1] Wang Y X. Design of composite structure. Beijing: Chemical Industry Press, 2001.(in Chinese)
王耀先. 复合材料结构设计.北京:化学工业出版社, 2001.
[2] Whitney J M,Sun C T.A higher order theory for extensional motion of laminated composites. Journal of Sound and Vibration, 1973, 30(1): 85-97.
[3] Reddy J N. A simple higher-order theory for laminated composite plates. Journal of Applied Mechanics, 1984, 51(4): 745-752.
[4] Stein M. Nonlinear theory for plates and shells including the effect of transverse shearing. Journal of AIAA, 1986, 24(9): 1537-1544.
[5] Kwon Y W, Akin J E. Analysis of layered composite plates using a higher-order deformation theory. Computers and Structures, 1987, 27(5): 619-623.
[6] Fu X H, Chen H R, Wang Z M. A refined higher-order theory and its finite element method for thick laminated plates. Acta Materiae Compositae Sinica, 1992, 9(2): 39-46.(in Chinese)
傅晓华, 陈浩然, 王震鸣. 复合材料多层厚板精化高阶理论及其有限元法. 复合材料学报, 1992, 9(2): 39-46.
[7] Li X Y, Liu D.Generalized laminated theories based on double superposition hypothesis.International Journal of Numerical Methods Engineering, 1997, 40(7): 1197-1212.
[8] Chandra R, Stemple A D, Chopra I. Thin-walled composite beams under bending, torsional and extensional loads. Journal of Aircraft, 1990, 27(7): 619-636.
[9] Jeon S M, Cho M H, Lee I. Static and dynamic analysis of composite box beams using large deflection theory. Computers & Structures, 1995, 57(4): 635-642.
[10] Wu Y P, Zhu Y L, Lai Y M, et al. Analysis of shear lag and shear deformation effects in laminated composite box beams under bending loads. Composite Structures, 2002, 55(2): 147-156.
[11] Vo T P, Lee J. Flexural-torsional behavior of thin-walled closed-section composite box beams. Engineering Structure, 2007, 29(8): 1774-1782.
[12] Wu Y P, Wang X J, Su Q, et al. A solution for laminated box beams under bending loads using the principle of complementary energy. Composite Structures, 2007, 79(3): 376-380.
[13] Vo T P, Lee J. Geometrically nonlinear analysis of thin-walled composite box beams. Computers and Structures, 2009, 87(3-4): 236-245.
[14] Vo T P, Lee J. Interaction curves for vibration and bucking of thin-walled composite box beams under axial loads and end moments. Applied Mathematical Modelling, 2010, 34(10): 3142-3157.
[15] Chakrabarti A, Sheikh A H, Griffith M, et al. Analysis of composite beams with partial shear interactions using a higher order beam theory. Engineering Structures, 2012, 34(3): 283-291.
[16] Rodman U, Saje M, Planinc I, et al. Exact buckling analysis of composite elastic columns including multiple delaminations and transverse shear. Engineering Structures, 2008, 30(6): 1500-1514.
[17] Han H T, Zhang Z, Lu Z X. Analytical method on bending of composite laminated beams with delaminations. Applied Mathematics and Mechanics, 2010, 31(7): 843-852.(in Chinese)
韩海涛, 张铮, 卢子兴. 含分层复合材料层合梁弯曲问题的一般解法. 应用数学与力学, 2010, 31(7): 843-852.
[18] Aslan Z, Sahin M. Buckling behavior and compressive failure of composite laminates containing multiple large delaminations. Composite Structures, 2009, 89(3): 382-390.
[19] Kim C, White S R. Analysis of thick hollow composite beams under general loading. Composite Structures, 1996, 34(3): 263-277.
[20] Kim C, White S R. Thick-walled composite beam theory including 3-D elastic effects and torsional warping. International Journal of Solids Structure, 1997, 34(31-32): 4237-4259.
[21] Zhong W X. The new solution system of elastic mechanics. Dalian: Dalian University of Technology Press, 1995.(in Chinese)
钟万勰.弹性力学求解新体系.大连:大连理工大学出版社, 1995.
[22] Wang X C. Finite element method. Beijing: Tsinghua University Press, 2003.(in Chinese)
王勖成.有限单元法.北京: 清华大学出版社, 2003.
AnalysisofthePerformanceofaBeamMadeofCompositeMaterialswithaGlueLayer
WANGDongfang,YANGJialing*
SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100191,China
Becausetheshearmodulusofacompositematerialisusuallyfarlessthanitselasticmodulus,shearresponseplaysagreatroleintheperformanceofabeammadeofcompositematerials,especiallyinthecaseofabeamwithlargesectionheight.Whenasquarepipebeammadeofcompositematerialssupportsastructuremembersuchasaglass-glue-glassstructure,thereisaweakergluelayerinthemiddleofthebeamflange.Inthiscase,complexwarpingwillbeproducedinthebeamcrosssectionbecauseofshearing.Basedonthepiecewiselineardisplacementfieldtheory,calculationmodelsofstaticanalysisandself-vibrationfrequencyaresetupforasquarepipebeammadeofcompositematerialsanddeformedwithinthesymmetryplane,andtheresultsarecomparedwiththosefromclassictheory.Thecalculationresultsinthispaperprovethatthegeometryparametersofthebeamandthemechanicalparametersofthegluelayerhavegreateffectontheperformanceofthebeam;inparticular,whentheglueisbyfarweakerthanthecompositematerial,theglueplaysadominantrole,andinthissituationtheclassicbeamtheoryisnotapplicable.
squarepipebeam;compositematerial;cross-sectionwarping;gluelayer;piecewiselinearity
2012-03-14;Revised2012-04-10;Accepted2012-04-24;Publishedonline2012-07-111704
URL:www.cnki.net/kcms/detail/11.1929.V.20120711.1704.003.html
NationalNaturalScienceFoundationofChina(11032001)
.Tel.:010-82317528E-mailJLYang@buaa.edu.cn
2012-03-14;退修日期2012-04-10;录用日期2012-04-24; < class="emphasis_bold">网络出版时间
时间:2012-07-111704
www.cnki.net/kcms/detail/11.1929.V.20120711.1704.003.html
国家自然科学基金(11032001)
.Tel.:010-82317528.EmailJLYang@buaa.edu.cn
WangDF,YangJL.Analysisoftheperformanceofabeammadeofcompositematerialswithagluelayer.ActaAeronauticaetAstronauticaSinica,2012,33(9):1655-1663. 王东方,杨嘉陵. 含胶层复合材料梁构件性能分析. 航空学报,2012,33(9):1655-1663.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
1000-6893(2012)09-1655-09
V414.8
A
王东方男, 博士研究生。主要研究方向: 冲击动力学。
Tel: 010-82338796
Email: east9235@163.com
杨嘉陵男, 博士, 教授, 博士生导师。主要研究方向: 冲击动力学。
Tel: 010-82317528
Email: JLYang@buaa.edu.cn

