基于关键装配特性的大型零部件最佳装配位姿多目标优化算法
朱绪胜, 郑联语
北京航空航天大学 机械工程及自动化学院, 北京 100191
基于关键装配特性的大型零部件最佳装配位姿多目标优化算法
朱绪胜, 郑联语*
北京航空航天大学 机械工程及自动化学院, 北京 100191
为了控制装配过程中的关键装配特性,以大尺寸测量技术为辅助,实现大型零部件最优位姿装配,提出基于关键装配特性的大型零部件最佳装配位姿多目标优化算法。该方法将测量辅助装配(MAA)中的关键环节——最佳装配位姿拟合问题分为两步:第1步利用基于奇异值分解的解析方法将测量坐标系与装配现场的全局坐标系进行精确的空间配准,减小了坐标系对齐的误差,并以参考点拟合的偏差为优化目标,求解移动装配体当前位姿;第2步根据装配关键特性相关公差的重要程度,计算装配综合精度要求,并以最小综合偏差为优化目标求解移动装配体间的最佳装配位姿。随后给出了上述两个步骤的粒子群优化算法模型,将每步的待求解位姿作为一个拥有3个旋转自由度与3个平移自由度的粒子进行求解。最后对卫星舱段位姿最优装配问题进行仿真计算,结果证明了该优化算法在控制各项关键特性、提高综合装配质量等方面的有效性。
关键特性; 大尺寸测量; 测量辅助装配; 位姿; 最优拟合; 粒子群算法
飞机、航天器、船舶、风力发电设备等大型产品的装配越来越依赖于大尺寸测量技术和仪器所提供的质量保证。上述产品的零部件尺寸大(如飞船舱段、飞机机身段等),多采用整体结构且精度要求越来越高,尤其是其中的关键特性(Key Characteristic, KC),如流体型面的轮廓度、对接同轴度、装配孔位置度、连接面的间隙等[1]。制造与装配过程中关键特性的微小偏差或波动会严重影响产品性能、降低效率并造成能源的大量消耗[2]。
关键装配特性,属于产品的几何关键特性,是指产品设计制造中的关键尺寸、形状和位置等几何要素要求, 是装配部门关注的质量特性。大型零部件装配中关键装配特性的波动控制直接决定装配质量,并将直接影响产品的使用性能[3]。因此,装配过程中零部件位姿的精确调整与关键特性控制是保证产品装配精度的核心问题,在部件对接、产品总装时更为突出。现在越来越多地依靠测量辅助装配(Measurement-Assisted Assembly,MAA)技术实现零部件装配的精确调姿,保证装配关键特性。测量辅助装配技术是先进数字化测量系统在产品数字化装配中的应用,综合应用了产品数字化定义、数字化模拟仿真、自动跟踪测量、自动化控制和机械随动定位等先进技术[4],利用大尺寸测量仪器对装配体各部件位姿参考点(基准点)跟踪测量,验证部件间相对位姿是否符合技术要求,并指导、调整各部件的位姿,完成装配。
当前,在航空航天等大型产品的测量辅助装配中主要采用激光跟踪仪或相机实现对零部件位姿的精确测量及调整。
在装配位姿调整方面,Marguet和Ribere介绍了测量辅助装配在Airbus总装中的使用,给出了测量辅助装配系统的组成部分及工作原理,但没有详细论述其中的核心技术——最佳装配位姿拟合方法[4]。邱宝贵等研制了大型飞机机身调姿与对接试验系统,通过激光跟踪仪测量试验机身上的检测点,集成管理系统计算机身的位姿,控制系统驱动多个三坐标数据控制器协同运动[5]。王少峰等提出了一种基于精密三坐标定位器四点支撑的大型飞机机身壁板装配位姿调整方法,将装配分为位置和姿态调整两个阶段,降低了多轴协调控制的难度[6]。上述研究中,对于装配精度的评价大多是基于参考点坐标值的偏差或单项公差来判断部件相对位姿是否满足要求,不够稳健和综合,在多项公差要求(关键特性)下最佳装配位姿的具体求解方法还未见报道。
在位姿测量技术方面,国内外学者也进行了不少研究,并提出了相应的位姿拟合算法。Beutler和Hanebeck基于解耦闭环极差姿态来计算目标位姿,提高了计算的精度[7]。Fischler和Bolls运用N点透视(PNP)在单目姿态解算,求解目标相对于相机的位姿参数[8]。Lowe提出了基于误差平方和最小的位姿求解方法[9]。Vincze等系统论述了基于激光跟踪的目标位姿的计算方法,提高了机器人末端定位的精度和速度[10]。Laroche和Kagami提出采用全景滚动快门照相技术进行位姿测量的动态模型,可以实时精确地捕捉目标位姿[11]。Matsubara等采用2台高性能电子相机组成测量系统,利用空间角交汇的原理计算目标的位姿[12]。许薇利用安装在动态平台上的图像采集系统进行平台的自主位姿测量[13]。张世杰等研究了利用4个非共面特征光学坐标和单光学测量敏感器的测量方法,给出了航天器间相对位姿参数的解析形式,满足了相对位姿精度和实时计算的要求[14]。以上成果多是针对单个测量目标的位姿求解以及提高拟合精度方法的优化,主要应用于航天器、机器人等动态载体,通过位姿计算,实现自主定位、跟踪,减小计算误差等功能,针对多项装配关键特性要求下大尺寸零部件装配过程中的最佳装配位姿拟合的研究未见报道。
针对上述问题,本文提出基于关键装配特性的最佳装配位姿拟合的多目标优化方法,力图对测量辅助装配中的关键问题进行深入研究,更好地保证关键装配特性要求,提高装配质量。
1 算法概述
1.1 问题描述
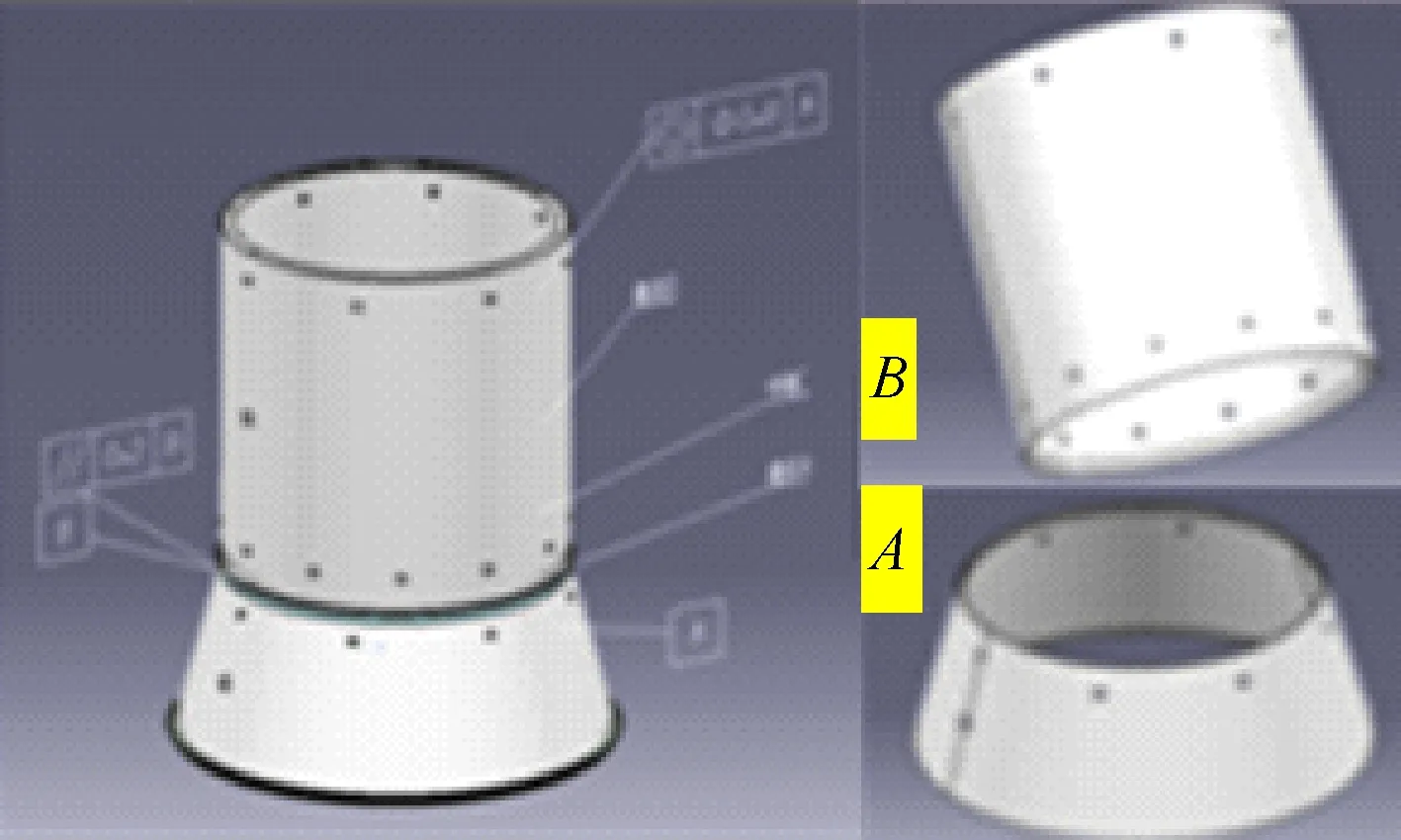
设两个大尺寸零部件处于对接装配阶段,基准装配体(Datum Component)已经固定在装配工装上,移动装配体(Movable Component)由装配辅助设备吊挂于装配现场某处,其装配示意图如图1所示。要求根据激光跟踪仪采集的参考点信息,求解满足关键装配特性各项公差的最佳装配位姿,指导装配工作。
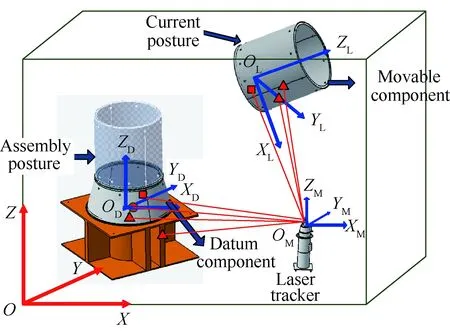
图1 卫星舱段装配示意图Fig.1 Schematic of satellite cabin assembly
为方便描述,定义后续计算中的坐标系如下:
1) 全局坐标系(Global Coordinate System, GCS),是装配的设计坐标系,在产品的装配过程仿真软件中定义,用O-XYZ表示。
2) 测量坐标系(Measurement Coordinate System, MCS),为工业测量系统软件默认的测量值基准坐标系,用OM-XMYMZM表示。
3) 移动装配体固联的局部坐标系(Local Co-ordinate System, LCS),在零部件CAD模型中定义,用OL-XLYLZL表示。
本文使用点的齐次坐标值Pi=[xiyizi1]T计算,测量点组坐标值表示为
(1)
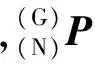
1.2 尺寸及形位公差的评定
如何利用分布在测量对象上的测量点信息合理评定测量对象的尺寸及形位公差,是以满足关键特性要求为优化准则的测量辅助装配技术必须要解决的问题。
尺寸及形位误差的评定可以使用评定对象上的测量点组的坐标值来实现[15-16]。
本文以同轴度误差评定作简要说明,如图2所示。利用坐标测量系统获取回转表面几个横截面上若干个点的坐标。以最小二乘法评定横截面圆轮廓,拟合每个横截面轮廓圆心。基准要素利用基准回转面上的横截面轮廓圆心点拟合基准轴线,再计算被测轮廓圆心到基准轴线的距离,最大距离乘以2即为同轴度误差,即:
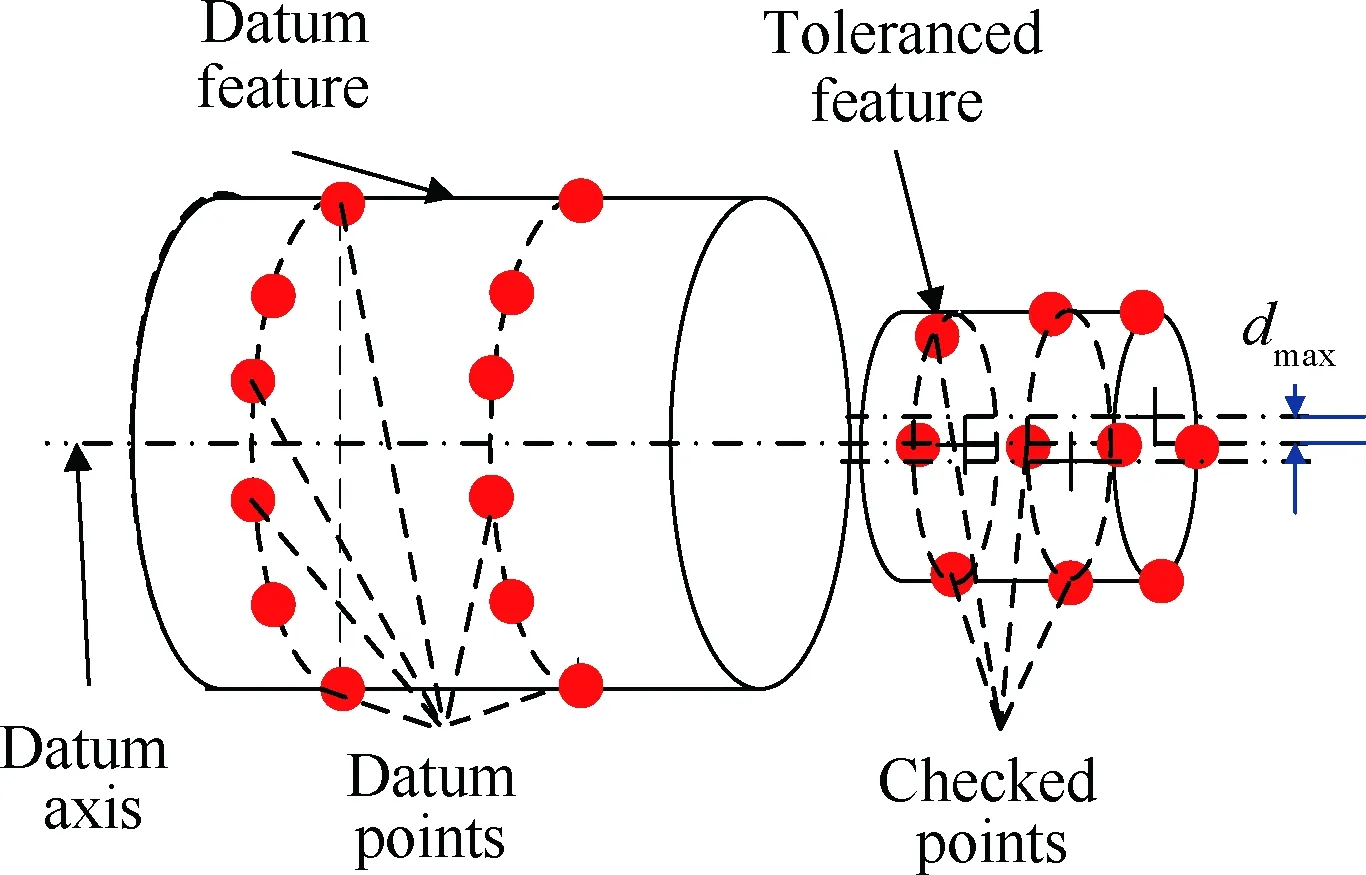
图2 同轴度误差评定Fig.2 Concentricity error calculation
f=2dmax
(2)
式中:dmax为被测轮廓圆心到基准轴线的最大距离。
装配过程中,当移动装配位于位姿M时,第I项检测项的误差εI可以利用固定装配体上的基准点(PID)及移动装配体上的参考点(PIM)的坐标,拟合需要的尺寸要素,可以计算出形位误差为
εI=fI(PID,PIM)
(3)
其他各类误差评定的方法可参阅文献[15]。
1.3 求解方案概述
将基于装配关键特性的最佳装配位姿拟合分为当前位姿拟合与最佳位姿拟合两个阶段进行求解,流程如图3所示。
步骤1当前位姿拟合:主要完成对测量设备(如激光跟踪仪)采集的参考点信息的数据空间配准,以及装配体当前位姿MC的拟合。
步骤2最佳位姿拟合:计算能合理表征关键装配特性多个公差要求的综合装配精度,然后以此作为指导,拟合最佳装配位姿M。
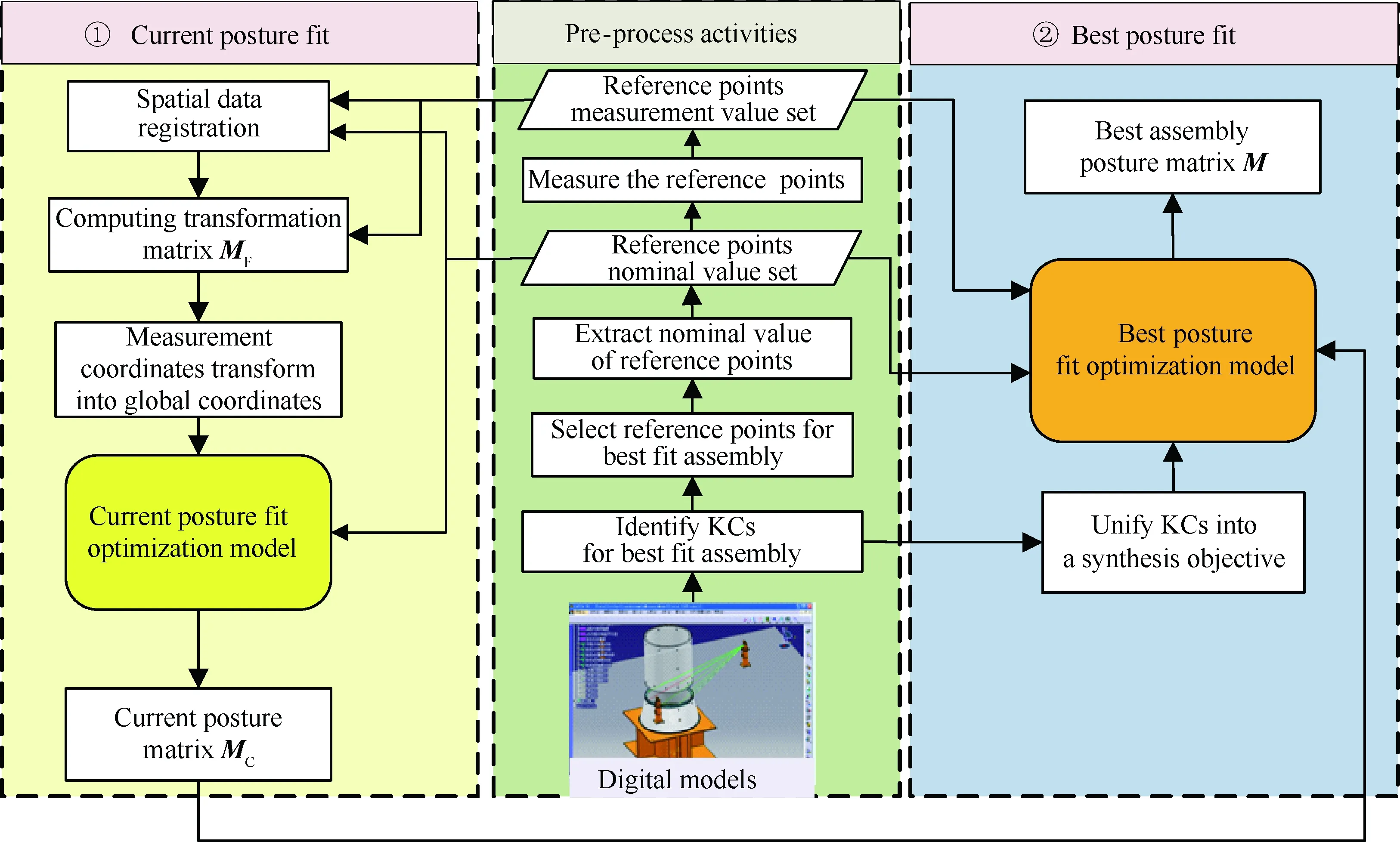
图3 算法流程Fig.3 Algorithm flowchart
在算法执行之前,需预先进行以下操作:①标识装配关键特性;②选择、定义装配关键特性相关的参考点;③在数字模型中提取参考点的名义局部坐标值;④测量基准装配体及移动装配体上定义的参考点,得到其三维坐标值。
2 当前位姿拟合
刚体的空间位姿,即位置与姿态,可由刚体固联局部坐标系与全局坐标系的3个自由度的旋转(α,β,γ)与3个自由度的平移(Tx,Ty,Tz)关系来表示。用T表示平移矩阵,R表示旋转矩阵,则刚体空间位姿M为
(4)
其中:
T3×1=[TxTyTz]T
(5)
(6)
2.1 坐标系优化配准
空间数据配准如图4所示,由于测量坐标系与全局坐标系不一致,须将测量值转换为全局坐标值,以备后续数据处理使用,转换矩阵用MF表示。
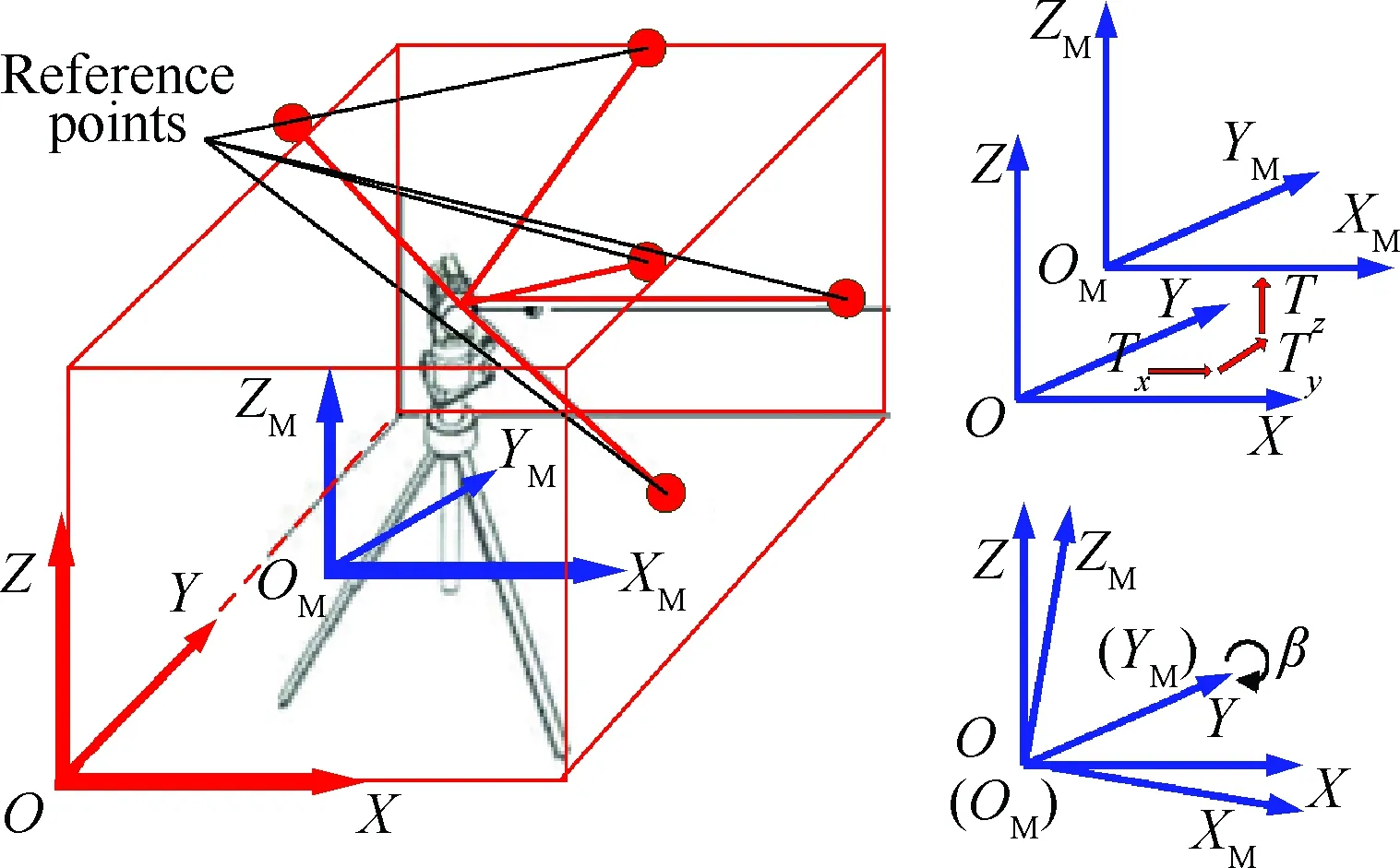
图4 空间数据配准Fig.4 Spatial data registration
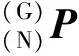
(7)
转换矩阵MF可通过3个基准点信息来求得,本文取n=5,以提高配准的精度及冗余度。为提高配准精度,采用基于奇异值分解的优化配准算法[17]。
参考点两组值具有相同的重心,这样可以先将平移矩阵T分离,求解旋转矩阵R。
1) 重心坐标为
(8)
(9)
重心化后的坐标分别为
(10)
(11)
则有
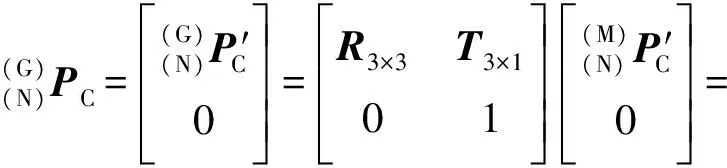
(12)
(13)
其中,参考点在测量坐标系下的名义坐标值可以近似地用测量坐标系下的实际测量值代替,但由于制造、测量的影响,造成坐标系配准时存在一定的偏差,使用ε表示,即
(14)
2) 目标函数表示为
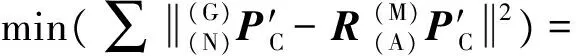
(15)
令
(16)
则上述问题等价于求max(tr(RH)),tr为矩阵的迹。
将H进行奇异值分解:
H=QTΛV
(17)
式中:Q和V为奇异值分解矩阵;Λ为对角矩阵。
则R的最优值为
R=VTQ
(18)
对应的平移向量为
(19)
2.2 移动装配体当前位姿拟合
通过参考点局部坐标值与全局坐标值的关系,可以拟合装配体当前位姿,如图5所示。
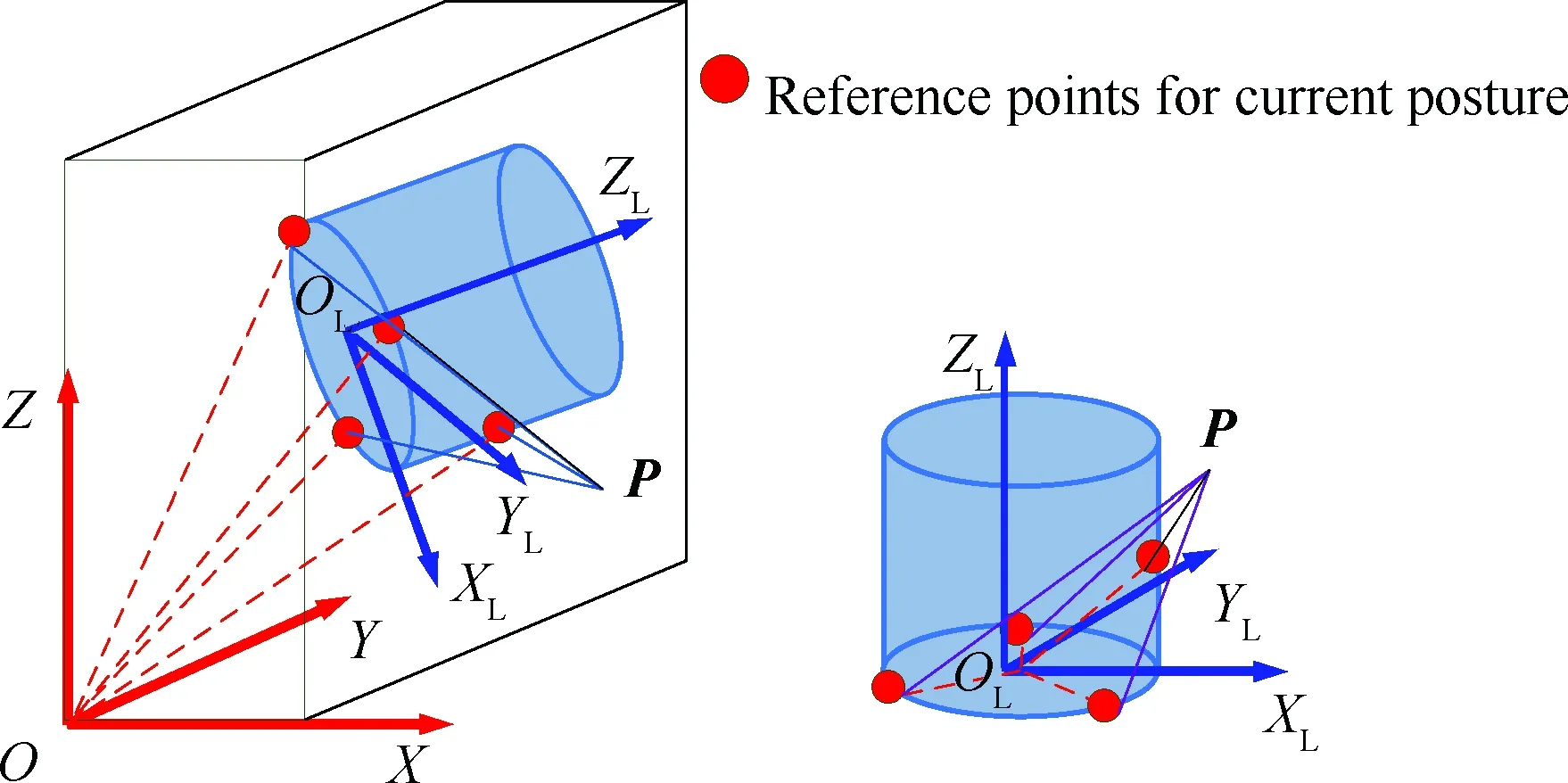
图5 当前位姿拟合示意图Fig.5 Schematic of current posture fit
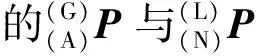
(20)
考虑制造及测量误差,参考点的名义值与实测值在匹配时的偏差用εi表示,i表示参考点的编号。则装配体位姿拟合可归结为以下优化问题:
(21)
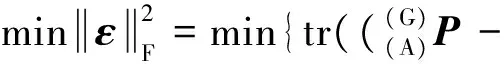
(22)
限制条件为
εlower≤εi≤εupper
(23)
式中:εlower、εupper分别为单点允许拟合偏差的上、下限。
3 最佳位姿拟合
3.1 最佳位姿拟合数学模型
为保证装配关键特性,在基准装配体位姿固定的情况下,需拟合移动装配体在全局坐标系下的最佳装配位姿,如图6所示。
装配中存在多项量纲不统一的尺寸及形位公差要求。本文以综合装配精度为优化目标将多目标统一,用综合偏差评价装配质量。综合偏差越小,装配精度越高,质量越好。首先,将各项偏差的严格程度划分为10个等级,W={1,2,…,10};
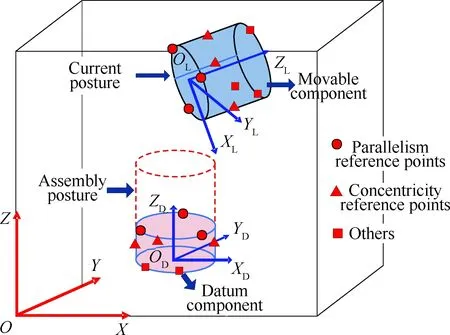
图6 最佳装配位姿拟合示意图Fig.6 Schematic of best assembly posture fit
然后以偏差对整体装配关键特性及性能的影响为指标,确定其对应的权重WI,WI∈W。
设I检测项误差为εI,则综合偏差E为
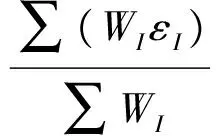
(24)
εI根据检测项类型及要求,调用相应偏差函数fI计算,由式(3)可知
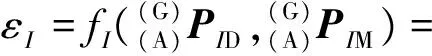
(25)
式中:PID为基准装配体上I检测项相关的测量点组坐标值;PIMC为移动装配体在当前装配位姿MC时,I检测项相关测量点组坐标值。
移动装配体姿态为M时,参考点坐标值为
(26)
则
(27)
最佳装配位姿等价于综合偏差最小,即
(28)
其中,要求各检测项的误差都要在允许范围内,
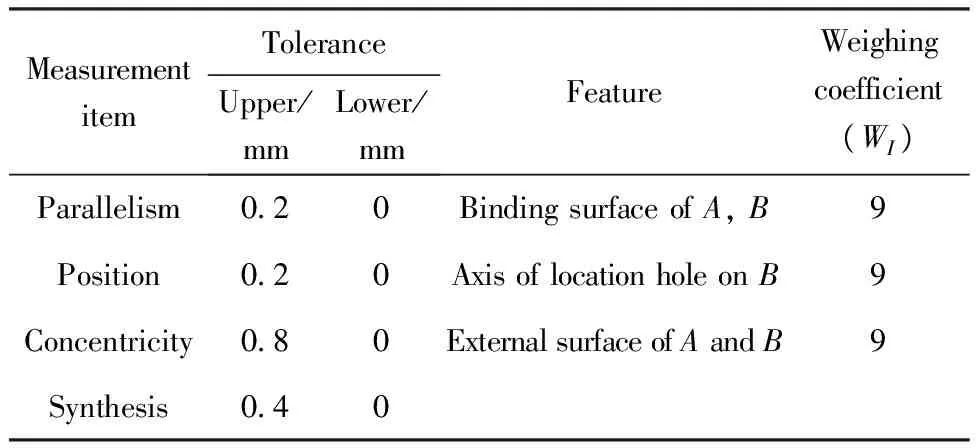
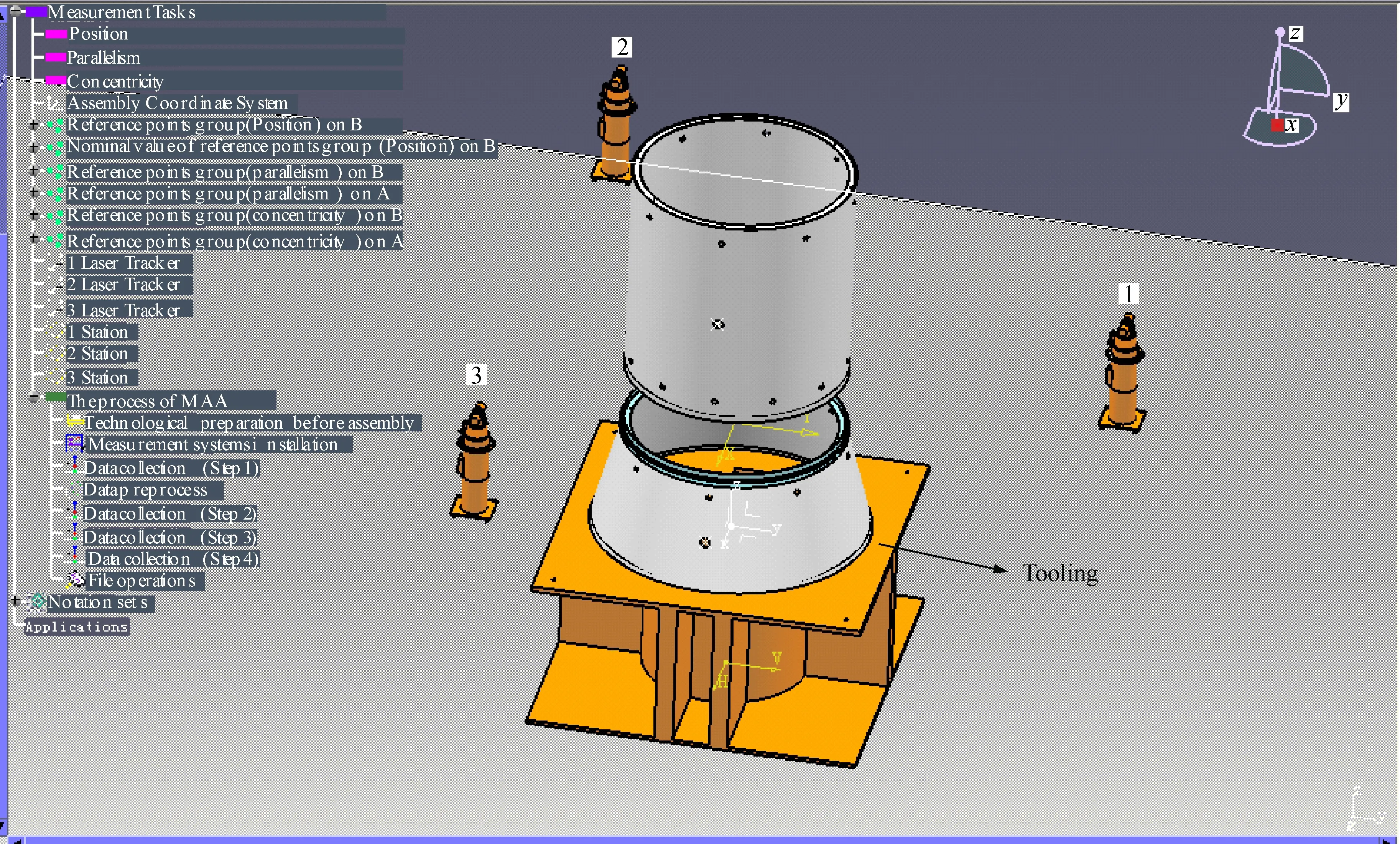
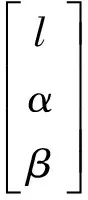
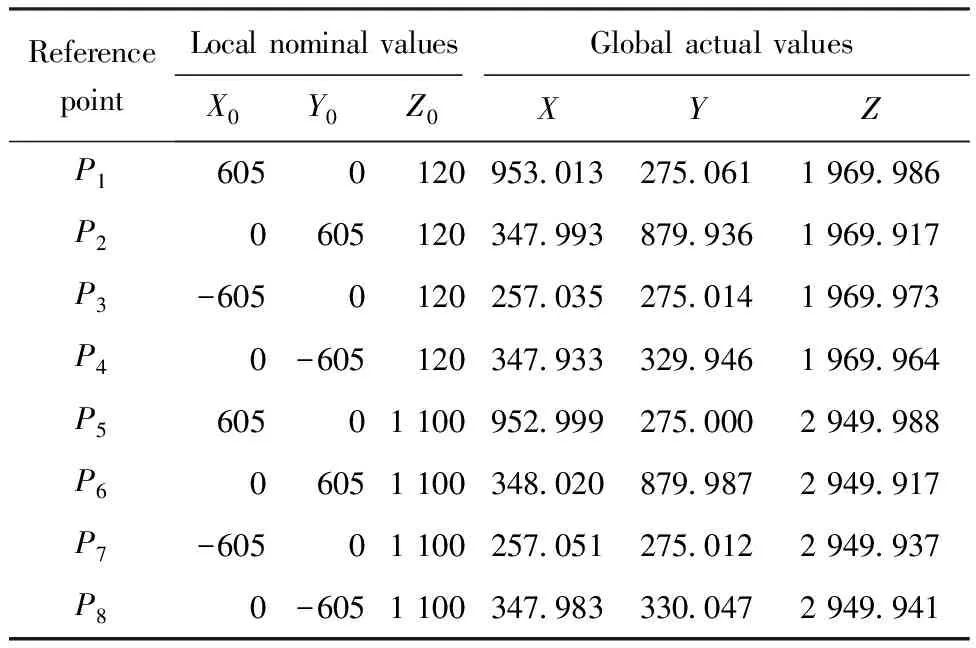
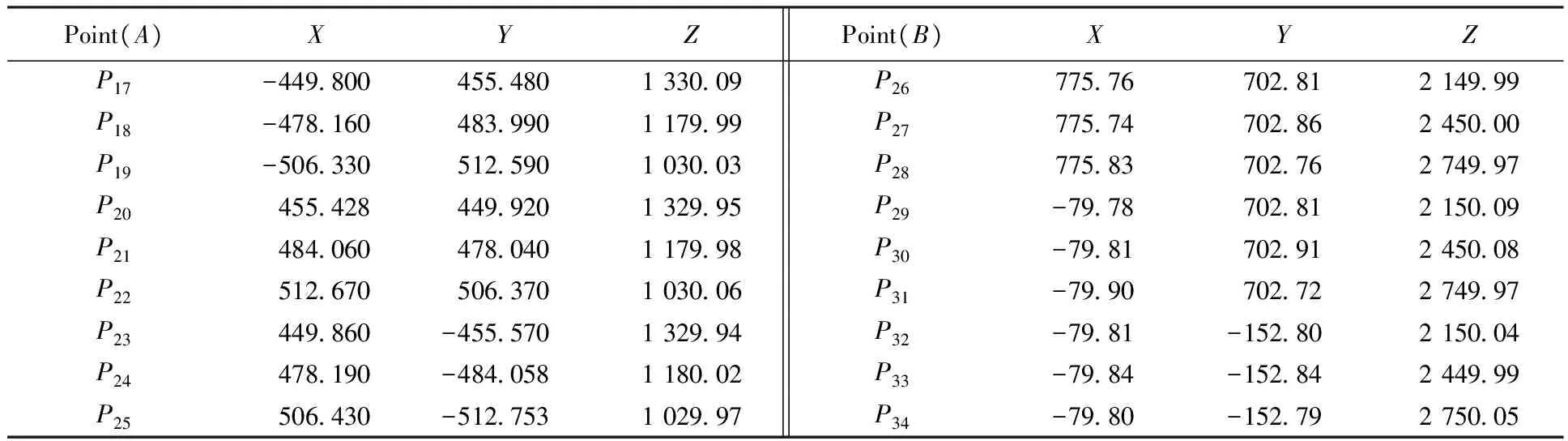
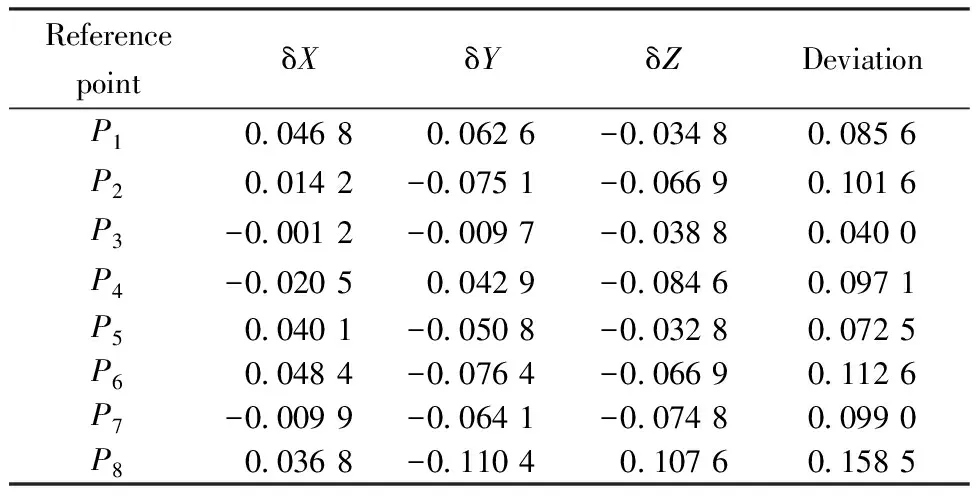
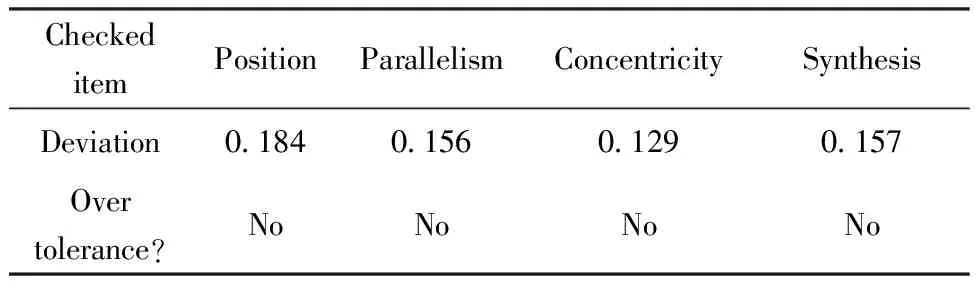
EI-lower<εI (29) 式中:EI-lower与EI-upper分别为I项公差的下限和上限。 3.2 粒子群优化算法流程 利用合粒子群算法求解两个过程时,将待求解的位姿作为一个粒子,其6个独立参数(Tx,Ty,Tz,α,β,γ)为粒子的维度,每个粒子包含一个位置向量xi与一个速度向量vi。粒子搜索解空间时,保存搜索到的最优经历位置pi=[pi1pi2…pi6],在每次迭代初,根据自身惯性和经验及群体最优经历位置pg=[pg1pg2…pg6],按以下公式来调整自己的速度向量以调整自身位置。 xi=xi+rvi (30) vi=wvi+c1ξ(pi-xi)+c2η(pg-xi) (31) 式中:r为对位置更新时的约束因子,此处取r=1;取加速因子c1=c2=2;ξ、η为[0,1]中均匀分布的随机数;w为惯性权重因子,此处采用线性递减策略对其进行赋值, w=Wmax-n(Wmax-Wmin)/N (32) 式中:Wmax与Wmin为w值的上下限;n为当前迭代次数;N为总迭代次数。这里取Wmax=0.95,Wmin=0.4,N=1 000。 粒子依据相应目标函数适应值,在约束空间内按照相应规律搜索,不断改变自身的位置、速度大小及方向,在满足算法终止条件下得出解[16,18]。两阶段粒子群算法流程,如图7所示。 步骤1将当前位姿MC的每个可行位置离散为拥有6个自由度的粒子随机解(3个移动自由度与3个旋转自由度)。 步骤2利用初始化的粒子群计算适应度函 数(见式(22)),根据适应度值确定个体极值pi和全局极值pg。 步骤3粒子根据个体极值及全局极值,利用式(30)和式(31)更新自己的速度与位置。 步骤4判断是否达到终止条件,即满足精度要求(见式(23))或达到最大迭代条件(N=1 000),得到当前位姿MC。 步骤5将最佳装配位姿的可行域离散为一群拥有6个自由度的粒子随机解,利用得到的MC、各参考点的坐标值及最佳装配位姿拟合的适应度函数(见式(28)),类似地重复步骤1~步骤4,在满足精度要求(见式(29))或达到最大迭代条件(N=1 000)时得到最佳装配位姿M。 图7 多目标最佳装配位姿拟合粒子群算法流程Fig.7 Multiple-objective assembly posture best fit based on particle swarm optimization diagram 本文以某卫星舱段(如图8所示)对接装配为例,验证算法的有效性,其中A作为基准装配体,B为移动装配体,装配相关的公差要求如表1所示。 图8 某卫星舱段Fig.8 Satellite cabin 位姿拟合仿真实验主要步骤如下:首先在CATIA环境下自主开发的集成大尺寸测量软件系统(Integrated Large Volume Measurement software System, I-LVMS)中获得卫星舱段的模型信息,进行测量规划(包括坐标系定义、测点规划、仪器布局等),然后使用激光跟踪仪仿真参考点的实测坐标值,最后利用MATLAB进行最佳装配位姿优化计算,并将结果反馈到I-LVMS系统。采用统一的测量数据集实现I-LVMS与MATLAB之间的集成。 表1 检测项参数列表Table 1 Parameter of inspection items 因为采用一个站位无法测量到所有参考点,所以实验采用3台API-T3激光跟踪仪,分别布置在如图9所示的站位,采集参考点坐标信息。此类型的激光跟踪仪长度测量的典型误差σl为10 μm/m,角度测量的典型误差为1″(σα=σβ)。 图9 虚拟仿真测量Fig.9 Measurement of virtual simulation 激光跟踪仪内部有一个测距传感器及两个测角传感器,可测得仪器到被测点的距离l,方位角α及天顶角β,转换为直角坐标值为 (33) 本仿真实验所采用的仿真测量数据,考虑到激光跟踪仪的测量误差,取为 (34) 式中:l*、α*和β*为测量CAD模型中提取的全局值对应的球坐标值;根据概率论的中心极限定理,每个传感器的误差εl、εα、εβ服从均值为0、标准差分别为σl、σα、σβ的正态分布。利用计算机产生符合概率分布的随机数,计算式(34),再根据式(33)的模型计算测量结果。循环上述步骤m次,得到测量结果的m个样本,对此样本进行统计运算得到仿真测量结果。参考点的仿真坐标信息如表2~表4所示。 表2装配体B位置参考点及位置度评估点坐标信息 Table2Informationofreferencepoints(assemblyBandposition) mm 表3 平行度测评点坐标信息Table 3 Information of reference points(parallelism) mm 表4 同轴度测评点坐标信息Table 4 Information of reference points(concentricity) mm 首先,根据装配体B上当前位姿拟合参考点的全局值与名义值(如表2所示),计算结果如图10所示,拟合移动装配体的当前位姿6个参数,结果如表5所示。其中,参考点平均位置偏差为0.108 mm,最大偏差为0.159 mm,如表6所示。然后,利用各项关键特性评估点的坐标信息(如表2~表4所示)进行最佳装配位姿求解,当装配体位于表7的位姿时,迭代结束,表8的结果表明,综合装配精度及各项偏差满足要求,为最佳装配位姿,结果如图11所示。 图10 当前位姿计算结果Fig.10 Results of current posture 图11 最佳装配位姿计算结果Fig.11 Results of best assembly posture 表5 装配体B当前位姿Table 5 Current posture of assembly B Tx/mmTy/mmTz/mmα/(10-3rad)β/(10-3rad)γ/(10-3rad)347972751850-30367-040107-12032 在实际舱段装配过程中,首先利用初始位置下各测量点的坐标信息,即可拟合得到移动装配体的当前位姿与最优装配位姿,结合二者设计并优化其移动路径,然后利用式(26)计算出对接过程中3~6关键点的目标坐标值,最后对关键点进行跟踪测量,通过驱动调姿机构(如基于高精密三坐标POGO柱三点支撑的大部件位姿调整机构等),及时修正移动装配体的运动路线,进而完成装配。 表6 参考点位置偏差Table 6 Deviation of reference points mm 表7 装配体B最佳装配位姿Table 7 Best assembly posture of assembly B 表8 检测项偏差Table 8 Inspection item errors mm 1) 利用基于奇异值分解的空间坐标系配准的优化,简化了计算过程,提高了数据拟合的精度,以拟合偏差矩阵的F-范数最小为优化目标,准确拟合移动装配体的当前位姿。 2) 根据各关键特性对整体的影响及重要程度设置权值,计算得到综合精度要求,并以此为目标,优化求解移动装配体的最佳装配位姿,提高了装配的质量和可靠性。 3) 运用该方法对某卫星对接装配采用仿真分析的方式进行最佳装配位姿求解,仿真结果验证了本文所提出的方法及模型的有效性。 4) 本方法适用于飞船舱段、飞机机身段等大型零部件测量辅助装配过程。针对不同装配任务,需重新定义、选择与装配关键特性相关的测量点。 5) 由于需要评估关键特性误差,因此本方法需要的测量点数目较多,但在实际位姿调整和跟踪测量过程中,可以选取其中的3~6关键点进行,从而实施测量辅助装配。 [1] Zheng L Y, McMahon C A, Li L, et al. Key characteristics management in product lifecycle management: a survey of methodologies and practices. Proceedings of the Institution of Mechanical Eegineerings, Part B: Journal of Engineering Manufacture, 2008, 222(8): 989-1008. [2] Thornton A C. Variation risk management: focusing quality improvements in product development and production. New Jersey: Wiley, 2004. [3] Carlson J S. How to redce geometrical variation in assembled products. Goteborg: Department of Mathematical Statistics, Chalmers University of Technology and Goteborg University, 2000. [4] Marguet B, Ribere B. Measurement-assisted assembly applications on airbus final assembly line. SAE Transactions, 2003, 112(1): 372-375. [5] Qiu B G, Jiang J X, Bi Y B, et al. Posture alignment and joining test system for large aircraft fuselages. Acta Aeronautica et Astronautica Sinica, 2011, 32(5): 908-919. (in Chinese) 邱宝贵, 蒋君侠, 毕运波, 等. 大型飞机机身调姿与对接试验系统.航空学报, 2011, 32(5): 908-919. [6] Wang S F, Zhang J H, Liu Z G, et al. Motion planning for posture alignment machine tool oriented fuselage panel. Journal of Xi’an Jiao Tong University, 2011, 45(3): 102-106. (in Chinese) 王少峰, 张进华, 刘志刚, 等. 大型飞机机身壁板装配位姿调整系统的运动规划. 西安交通大学学报, 2011, 45(3): 102-106. [7] Beutler F, Hanebeck U D. Closed-form range-based posture estimation based on decoupling translation and orientation. 2005 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2005, 4: 989-992. [8] Fischler M A, Bolls R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communication of the ACM, 1981, 24(6): 381-395. [9] Lowe D G. Fitting parameterized three-dimensional models to images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(5): 441-450. [10] Vincze M, Prenninger J P, Gander H. A laser tracking system to measure position and orientation of robot end effectors under motion. The International Journal of Robotics Research, 1994, 13(4): 305-314. [11] Laroche E, Kagami S. Dynamical models for position measurement with global shutter and rolling shutter cameras. 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2009: 5204-5209. [12] Matsubara H, Tsukada T, Ito H, et al. A three dimensional position measurement method using two pan-tilt cameras. R&D Review of Toyota CRDL, 2003, 38(2): 43-49. [13] Xu W. Study on the self-measuring method of the attitude and position based on geometrical characteristic parameter. Tianjin: College of Precision Instrument & Optic-Electronics Engineering, Tianjin University, 2008. (in Chinese) 许薇. 基于几何特征量的自主位姿测量方法的研究. 天津: 天津大学精密仪器与光电子工程学院, 2008. [14] Zhang S J, Cao X B, Chen X Q. Closed-form method for relative pose parameters of spacecraft based on optical measurement. Acta Aeronautica et Astronautica Sinica, 2005, 26(2): 214-218. (in Chinese) 张世杰, 曹喜滨, 陈雪芹. 航天器相对位姿参数光学测量解析算法. 航空学报, 2005, 26(2): 214-218. [15] Weber T, Motavalli S, Fallahi B, et al. A unified approach to form error evaluation. Precision Engineering, 2002, 26(3): 269-278. [16] Ni A J, Zheng L Y. Optimal configuration method for large-scale measurement systems based on form error uncertainty. Acta Metrologica Sinica, 2011, 32(4): 289-295. (in Chinese) 倪爱晶, 郑联语. 基于形状误差不确定度的大尺寸测量系统优化配置方法. 计量学报, 2011, 32(4): 289-295. [17] Zhang F M, Qu X H, Ye S H. Multiple sensor fusion in large scale measurement. Optic and Precision Engineering, 2008, 16(7): 1236-1240.(in Chinese) 张福民, 曲兴华, 叶声华. 大尺寸测量中多传感器的融合. 光学精密工程, 2008, 16(7): 1236-1240. [18] Shi Y. Particle swarm optimization: developments, applications and resources. Proceedings of the 2011 Congress on Evolutionary Computation, 2001, 1: 81-86. Multiple-objectiveOptimizationAlgorithmBasedonKeyAssemblyCharacteristicstoPostureBestFitforLargeComponentAssembly ZHUXusheng,ZHENGLianyu* SchoolofMechanicalEngineeringandAutomation,BeihangUniversity,Beijing100191,China Tocontrolthekeyassemblycharacteristicsandattainthebestfitofposturewiththeaidoflarge-scalemeasurement,amultiple-objectiveoptimizationalgorithmisproposedbasedonkeyassemblycharacteristicstoposturebestfitforlargecomponentassembly.Thisapproachregardstheposturebestfit,whichisakeyactivityoflargecomponentassemblyinmeasurement-assistedassembly(MAA),asatwo-phaseoptimalproblem.Inthefirstphase,themeasurementcoordinatesystemandtheglobalcoordinatesystemareunifiedwithminimumerrorbasedonsingularvaluedecomposition,andthecurrentpostureofthecomponentsbeingassembledisoptimallysolvedintermsoftheminimumvariationofallthereferencepoints.Inthesecondphase,thesyntheticerrorrequirementofassemblyiscomputedaccordingtotheimportanceofeverykeyassemblycharacteristictothewholeproduct,andthebestpostureofthemovablecomponentsareoptimallydeterminedbyminimizingthesyntheticerror.Thentheoptimalmodelandtheprocessproceduresforthetwophasesbasedonparticleswarmoptimizationareproposed.Inthismodel,eachposturetobecalculatedismodeledasasixdimensionalparticle(withthreemovementandthreerotationparameters).Finally,anassemblyexampleaboutthejoiningoftwocabinsectionsofasatellitemainframestructureisperformedtoverifytheeffectivenessoftheproposedapproachandprocessalgorithm.Theexperimentresultshowsthatthealgorithmisrobustandeffectivetocontroleverykeyassemblycharacteristicandimprovetheassemblyquality. keycharacteristics;large-scalemeasurement;measurement-assistedassembly;posture;bestfit;particleswarmoptimization 2012-03-12;Revised2012-04-07;Accepted2012-05-22;Publishedonline2012-09-030956 URL:www.cnki.net/kcms/detail/11.1929.V.20120903.0956.001.html NationalNaturalScienceFoundationofChina(51175026) .Tel.:010-82317725E-maillyzheng@buaa.edu.cn 2012-03-12;退修日期2012-04-07;录用日期2012-05-22; < class="emphasis_bold">网络出版时间 时间:2012-09-030956 www.cnki.net/kcms/detail/11.1929.V.20120903.0956.001.html 国家自然科学基金(51175026) .Tel.:010-82317725E-maillyzheng@buaa.edu.cn ZhuXS,ZhengLY.Multiple-objectiveoptimizationalgorithmbasedonkeyassemblycharacteristicstoposturebestfitforlargecomponentassembly.ActaAeronauticaetAstronauticaSinica,2012,33(9):1726-1736. 朱绪胜,郑联语.基于关键装配特性的大型零部件最佳装配位姿多目标优化算法.航空学报,2012,33(9):1726-1736. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 1000-6893(2012)09-1726-11 V262.4 A 朱绪胜男, 博士研究生。主要研究方向: 数字化设计与制造, 数字化测量与质量控制。 E-mail: zhuxusheng@me.buaa.edu.cn 郑联语男, 博士, 教授, 博士生导师。主要研究方向: 数字化设计与制造、 数字化测量与质量控制和数字企业技术等。 Tel: 010-82317725 E-mail: lyzheng@buaa.edu.cn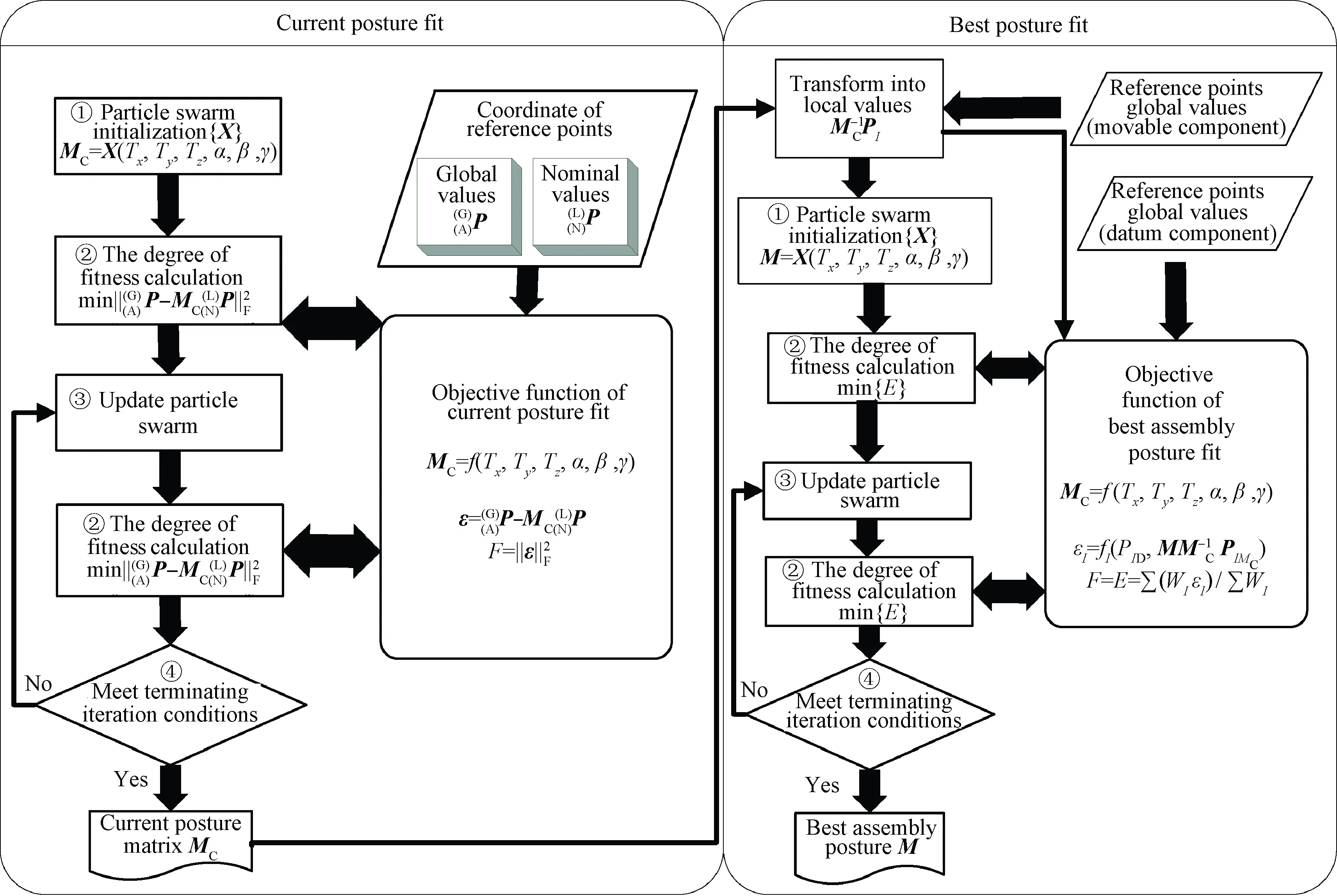
4 案例验证与分析
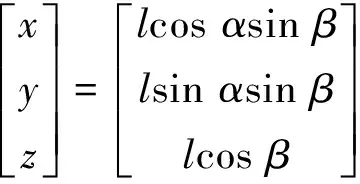




5 结 论

