锥度量空间中一类压缩映射不动点定理.

胡松林, 姚小杰, 胡长松

(湖北师范学院 数学与统计学院, 湖北 黄石 435002)

0 引言

在非线性分析中Banach 压缩原理是非常有用的一个结果，在度量空间我们可以如下表示.

定理1 设(X，d) 为一个完备的度量空间，T:X→X是一个压缩映射，即存在0 ≤r< 1 使得

d(Tx，Ty) ≤ rd(x，y) ∀x,y∈X

(1)

则T在X中存在一个唯一的不动点.

定理1在解决非线性方程中有很多的应用， 它的推广分为直接推广和局部的推广.近几年Tomonari Suzuki[1～3][5～6]推广了Banach 压缩原理发现了一类新的压缩条件下的不动点定理, 另外在[7]中是一些最近的公共不动点定理， 最近Misako Kikkawaa 和Tomonari Suzuki 也证明了下面一个不动点定理.

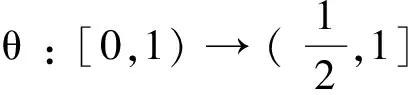
(2)

设(X,d) 为一个完备的度量空间，T定义在X上的映射满足下述条件。

假设存在r∈ [0,1) 使得

θ(r)d(x,Tx) ≤d(x,y) ⟹d(Tx,Ty) ≤rd(x,y)

(3)

对任意的x,y∈X, 则T存在一个唯一个不动点.

在这篇文章中将定理2 推广到了锥度量空间中，证明了一个新的不动点定理.

1 预备知识

锥度量空间是在参考文献[4]中引进的，作者描述了锥度量空间中收敛与完备性，并且在锥度量空间中证明了一些压缩映射的不动点定理.最近在[7～8]中是锥度量空间中的公共不动点定理.下面给出[4]中的一些锥度量空间的定义：

令E为实Banach空间，当且仅当满足下列条件，E上的子集P称为锥：

a)P是非空闭集；

b)a,b∈R;a,b≥0,由x,y∈P可以推出ax+by∈P;

c)P∩(-P) = 0.

我们在锥P中定义一个半序，用符号≤表示，x≤y指y-x∈P.x0使得x,y∈E.

0 ≤x≤y等价于‖x‖ ≤K‖y‖

满足不等式的最小正数称为锥P的正规常数，显然K≥1.由[4]知道在Banach空间中非空的正规锥是存在的.关于锥度量空间的定义和数列收敛性详细见参考文献[4].

2 主要结论

在证明我们的主要结果时将用到下面的引理.

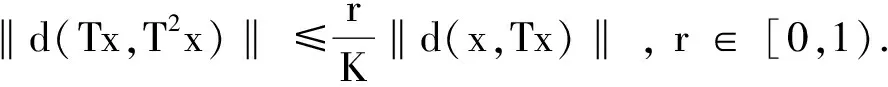
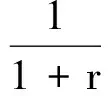
必有一个成立.

证 反证法，假设

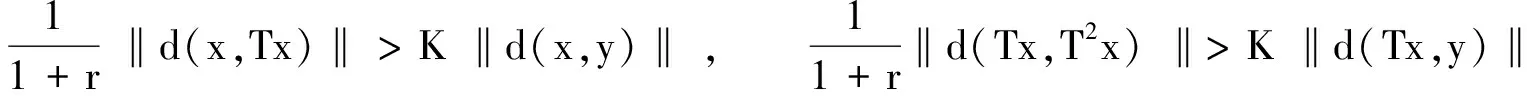
则

‖d(x,Tx)‖ ≤K‖d(x,y)‖ +K‖d(y,Tx)‖<

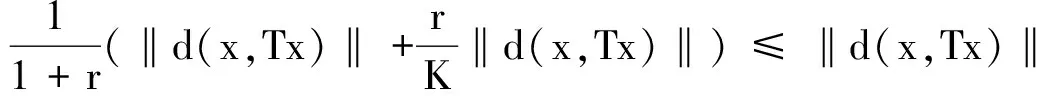
矛盾.完成引理证明.

以下就是我们的主要结论。

定理3 由(2) 定义一个不增的函数θ.设(X,d) 为完备的锥度量空间，正规锥P的常数为K.T定义在X上的映射,假设存在r∈ [0,1) 使得

θ(r) ‖d(x,Tx)‖ ≤K‖d(x,y)‖

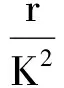
(4)

对任意的x,y∈X, 则T存在唯一不动点.

证 因为θ(r) ≤ 1,θ(r) ‖d(x,Tx)‖ ≤K‖d(x,Tx)‖.因此由假设条件可得对于任意的x∈X有

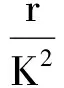
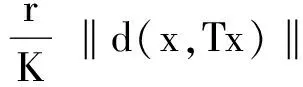
(5)

任取u∈X.令u0=u,un=Tnu, ∀n∈N.则有un+1=Tun.通过(2)式, 我们有

下面我们来证明un是cauchy 列,由三角不等式，当n>m有

d(un,um) ≤d(un,un-1) +d(un-1,un-2) + … +d(um+1,um)

(6)

又因为P是正规的.所以

‖d(un,um)‖ ≤K‖d(un,un-.1) +d(un-1,un-2) + … +d(um+1,um)‖≤

K(‖d(un,un-1)‖ + ‖d(un-1,un-2)‖ + … + ‖d(um+1,um)‖)

由(6) 式

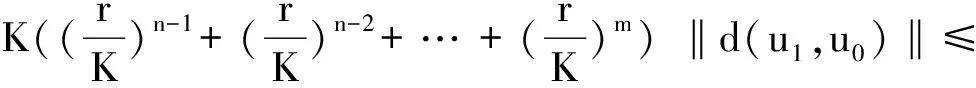
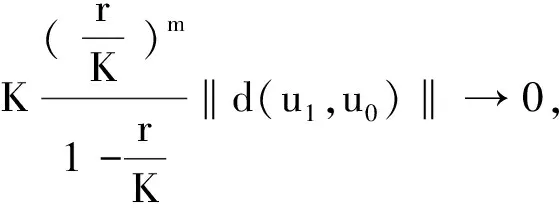
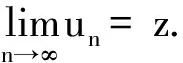
下证

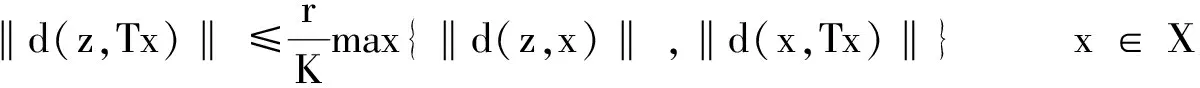
(7)

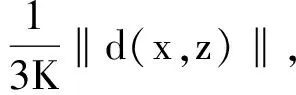
θ(r) ‖d(un,Tun)‖ ≤ ‖d(un,Tun)‖= ‖d(un,un+1)‖≤

K‖d(un,z)‖ +K‖d(z,un+1)‖≤

‖d(x,z)‖ -K‖d(un,z)‖ ≤K‖d(un,x)‖

则由假设有

‖d(Tun,Tx)‖ ≤

因此对于∀x∈X,Tx≠z有

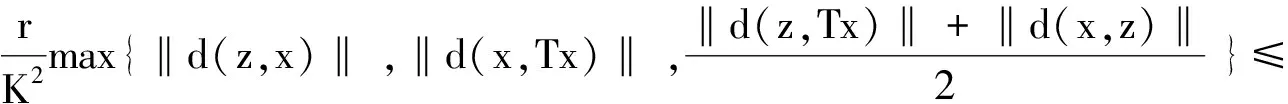
下证z是T的不动点, 我们分以下3 种情况讨论:

第一种情况， 有反证法假设Tz≠z, 如果Tz=z, 完成定理证明.

假设Tkz≠z，∀k≥ 2.如果Tkz=z, 由‖d(z,Tz)‖ =d(Tkz,Tk+1z) ≤rk‖d(z,Tz)‖矛盾.特别有TTTz≠z,TT≠z.因此有TTTz≠z,TT≠z和Tz=Tz≠z.利用(5)(7) 式, 可得

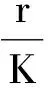
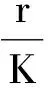
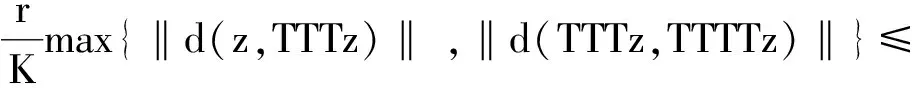
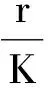
(8)

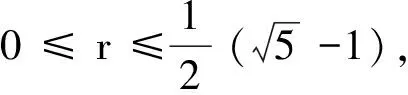
θ(r)d(TTz,TTTz) ≤d(TTz,z)

(9)

如果不成立即有K‖d(TTz,z)‖ < ‖d(TTz,TTTz)‖, 利用(5) 式有

‖d(Tz,z)‖ ≤K‖d(Tz,TTz)‖ +K‖d(TTz,z)‖<

K‖d(Tz,TTz)‖ + ‖d(TTz,TTTz)‖≤

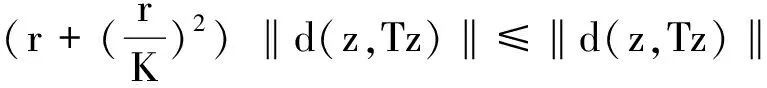
所以矛盾.因此(9) 式成立.因此由条件假设有

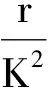
(10)

利用同样的方法我们有

(11)

利用(8),(11), 有

‖d(Tz,z)‖≤K‖d(Tz,TTTTz)‖ +K‖d(TTTTz,z)‖≤

即矛盾， 所以Tz=z.

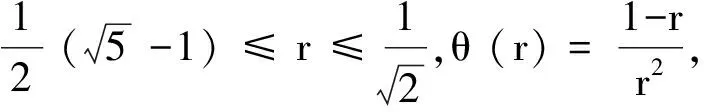
θ(r)d(Tk+1z,Tk+2z) ≤d(Tk+1z,z) ∀k∈N

(12)

利用用归纳假设法, 当k=1.如果(12) 式不成立, 由(5)式有

d(z,Tz) ≤d(z,TTz) +d(TTz,Tz)<

θ(r)d(TTz,TTTz) +d(TTz,Tz)≤

(θ(r)r2+r)d(z,Tz) ≤d(z,Tz)

矛盾，所以(12) 成立, 因此(10) 成立.假设k≤L成立, 由条件假设有,

d(Tk+2z,Tz) ≤rd(z,Tz) ∀k≤L

下面我们证明k=L+1也成立.如果(12) 式不成立, 由(7) 式有,

‖d(z,Tz)‖ ≤K‖d(z,TTz)‖ +K‖d(TTz,Tz)‖<

θ(r) ‖d(TTz,TTTz)‖ +K‖d(TTz,Tz)‖≤

矛盾，所以(12) 成立, 因为(10)式成立，利用归纳法假设k≤L成立,

证明k=L+1成立，如果不成立由(5)

‖d(z,Tz)‖ ≤K‖d(z,TL+2z)‖ +K‖d(TL+2z,Tz)‖ <

θ(r)d(TL+2z,TL+3z) +Kd(TL+2z,Tz)‖ ≤

(13)

利用(8)(13) 有

d(Tz,z) ≤K‖d(Tz,Tk+1z) ‖+K‖d(Tk+1z,z) ≤

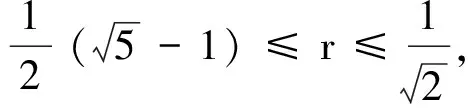
所以

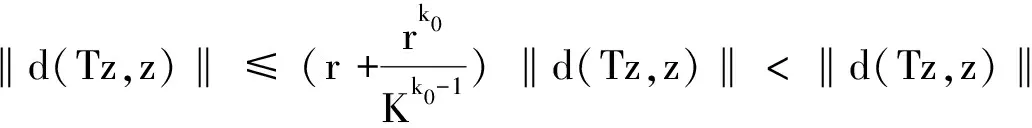
矛盾，所以Tz=z.

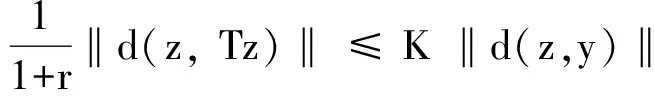
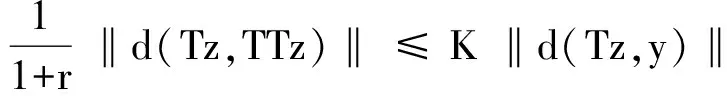
‖d(z,Tz)‖ ≤K‖d(z,TTz)‖ +K‖d(TTz,Tz)‖≤r‖d(z,Tz)‖

所以Tz=z.

因此在三种情况下z都是T的不动点.

下面证明不动点是唯一的.假设y是T的不动点.因为θ(r) ‖d(z,Tz)‖=0≤K‖d(z,y)‖由条件假设有

‖d(z,y)‖=‖d(Tz,Ty)‖≤

因此z=y.完成定理证明.

参考文献:

[1]Kikkawa M,Suzuki T.Three fixed point theorems for generalized contractions with constants in complete metric spaces[J].Nonlinear Analysis,2008,69:2942～2949.

[2]Suzuki T.Characterizations of fixed points of nonexpansive mappings[J]． J Math Sci, 2005,1723～1735.

[3]Suzuki T.A new type of fixed point theorem in metric spaces[J]．Nonlinear Analysis,2009,doi:10.1016/j.na.2009.04.017.

[4]Huang L G, Zhang X.Cone metric spaces and fixed point theorems of contractive mappings[J]． J Math Anal Appl,2007,332 (2) :1468～1476.

[5]Suzuki T.Generalized distance and existence theorems in complete metric spaces[J]． J Math Anal Appl,2001,253:440～458.

[6]Suzuki T.Contractive mappings are Kannan mappings, and Kannan mappings are contractive mappings in some sense[J]．Commentationes Mathematica，Prace Matematyczne, 2005,45(1):45～58.

[7]Abbas M, Jungck G.Common fixed point results for noncommuting mappings without continuity in cone metric spaces[J]．J Math Anal Appl,2008,341:416～420.

[8]Rezapour Sh, Hamlbarani R.Some notes on the paper "Cone metric spaces and fixed point theorems of contractive mappings"[J]．J Math Anal Appl,2008,345:719～724.