伴随矩阵在射影几何中的应用

吴利斌，詹 鸿

(武汉软件工程职业学院 公共课部，湖北 武汉 403205)

1 伴随矩阵的定义及其性质

定义1 设Aij为n阶矩阵

中元素aij的代数余子式，则称矩阵

为矩阵A的伴随矩阵.

定理1 设A*为n阶可逆矩阵A的伴随矩阵，则有

1)AA*=A*A=|A|E，其中|A| 为矩阵A的行列式，E为n阶单位矩阵；

2) (kA)*=k-1A*，其中k为非零常数；

3) (A*)T=(AT)*，其中AT为矩阵A的转置矩阵；

4) (A*)*=|A|n-1A，其中n≥2 .

2 伴随矩阵在射影平面的射影对应中的应用

2.1 伴随矩阵在射影平面的直射(同素)对应中的应用

定义2 两平面的点之间的一一对应若保持点和直线的结合性，且使任何共线四点的交比等于其对应四点的交比，则称此一一对应为两平面点之间的射影对应.

定义3 两平面的直线之间的一一对应若保持点和直线的结合性，且使任何共点四直线的交比等于其对应四直线的交比，则称此一一对应为两平面直线之间的射影对应.

定义4 上面定义的两种射影对应都称为两平面之间的直射(同素)对应.

定义5 如果两对应平面是重合的，则上面定义的射影对应和直射(同素)对应分别为此平面上的射影变换和直射(同素)变换.

由上面的定义，易得

定理2 若在两平面π与π′内各建立射影坐标系，则平面π到π′上的点之间的射影对应为非奇线性对应

f:ρx′=Ax,ρ|A|≠0

(1)

定理3 若在两平面π与π′内各建立射影坐标系，且平面π到π′上的点之间的射影对应为(1)，则平面π′到π上的点之间的射影对应为非奇线性对应

f-1:σx=A*x′,σ|A*|≠0

(2)

证明 由于|A|≠0，则A可逆，用A的逆矩阵A-1=|A|-1A*左乘(1)式两边得ρ-1|A|x=A*x′ ，令ρ-1|A|=σ，则得f-1:σx=A*x′.由定理1可得 |A*|=|A|2，故σ|A*|=ρ-1|A||A|2=ρ-1|A|3≠0.

定理4 若在两平面π与π′内各建立射影坐标系，且平面π到π′上的点之间的射影对应为(1)，则平面π到π′ 上的直线之间的射影对应为非奇线性对应

g:λu′=A*Tu,λ|A*T|≠0

(3)

证明 设任意直线l:uTx=0,经射影对应(1)变为对应直线l′:u′Tx′=0，将射影对应(1)的逆对应(2)代入直线l的方程得uT(σ-1A*x′)=0，即(uTA*)x′=0，或 (A*Tu)Tx′=0，与对应直线l′ 的方程比较，即得g:λu′=A*Tu，且λ|A*T|=λ|A|2≠0.

定理5 若在两平面π与π′内各建立射影坐标系，且平面π到π′上的点之间的射影对应为(1)，则平面π′到π上的直线之间的射影对应为非奇线性对应

g-1:μu=ATu′,μ|AT|≠0

(4)

证明 由定理1，可得 (A*T)-1=(AT*)-1=((AT)-1)*=(|AT|-1AT*)*=|A|-1AT，由(3)得u=λ(A*T)-1u′=λ|A|-1ATu′，令μ=λ-1|A| ，即得g-1:μu=ATu′ ，且μ|AT|=λ-1|A|2≠0.

2.2 伴随矩阵在射影平面的对射(异素)对应中的应用

定义6 若平面π的点x到π上的直线u之间的一一对应满足非奇线性对应

h:φu=Ax,φ|A|≠0

(5)

则称此对应为平面 上的点与直线之间的对射(异素)对应(变换).

定理6 若平面π上的点与直线之间的对射(异素)对应(变换)为(5)，平面π上的直线与点之间的对射(异素)对应(变换)为

h-1:θx=A*u,θ|A*|≠0

(6)

证明 由于|A|≠0，由(5)整理得φ-1|A|x=A*u，令φ-1|A|=θ，则得h-1:θx=A*u，且θ|A*|=φ-1|A||A*|=φ-1|A|3≠0.

定理7 若h1,h2是平面π上的对射(异素)变换，则h1·h2是平面π上的直射(同素)变换.

定义7 设h是平面π上的一个对射(异素)变换，若其平方是恒等变换(即h2=I)，则称h为平面π上的配极变换.且点x对应的直线u称为点x的极线，直线u对应的点x称为直线u的极点.

3 伴随矩阵在二次曲线射影理论中的应用

定义8 在射影平面上，齐次坐标 (x1,x2,x3)满足

xTAx=0

(7)

的点的集合称为二阶曲线.其中x=(x1,x2,x3)T，且A=(aij) 为三阶非零对称矩阵.

若A=(aij) 为三阶可逆的对称矩阵，则称此二阶曲线为非退化的二阶曲线.

定义9 在射影平面上，齐次线坐标[u1,u2,u3] 满足

uTA′u=0

(8)

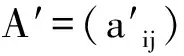
定义10 二阶曲线和二级曲线统称为二次曲线.

定理8 一条非退化的二阶曲线的切线的集合是一条非退化的二级曲线.且若非退化的二阶曲线为

xTAx=0

(7)

则其对应的二级曲线为

uTA*u=0

(9)

证明 由二阶曲线的极点与极线的关系得

ρu=Axρ|A|≠0,AT=A

(10)

又由二阶曲线的切线u通过其极点x得

uTx=0

(11)

由(10)得x=ρ|A|-1A*u，将其代入(11)得ρ|A|-1uTA*u=0，由ρ|A|-1≠0即得(7)对应的二级曲线为uTA*u=0.

由定理8的证明过程即得

定理9 一条非退化的二级曲线的切点的集合是一条非退化的二阶曲线.且若非退化的二级曲线为

uTA′u=0

则其对应的二阶曲线为 .

xTA′*x=0

(12)

注 若非退化的二级曲线为

uTA*u=0

则其对应的二阶曲线为

xTAx=0

事实上，由二级曲线的极线与极点的关系得

σx=A*u

(13)

又由二级曲线的直线通过其极点x得

xTu=0

(14)

由(13)得u=σ(A*)-1x=σ(|A|A-1)-1x=σ|A|-1Ax，将其代入(14)得σ|A|-1xTAx=0，即得(9)对应的二阶曲线为xTAx=0.

参考文献：

[1]王萼芳.高等代数[M].北京：高等教育出版社，2009.

[2]樊 恽，钱吉林，岑嘉评，等.代数学辞典[M].武汉： 华中师范大学出版社，1994.

[3]梅向明，刘增贤，王汇淳，等.高等几何[M].北京：高等教育出版社，2008.

[4]龙泽斌.几何变换[M].长沙：湖南科学技术出版社，1983.