定积分在证明初等不等式中的应用

余盛利，程 舰(湖北师范学院 数学与统计学院，湖北 黄石 435002)

不等式在数学中占有重要地位。而证明不等式的方法多种多样，数学上常用的解题方法基本上都可用来证明不等式，又由于不等式本身的完美性以及证明的困难性，使得不等式成为数学竞赛和高考的重点内容之一。有些不等式，尤其是初等超越不等式，用初等数学中熟知的方法和技巧难以证明。本文利用定积分的概念、几何意义及其性质证明初等不等式，方法巧妙、证明简捷。下面就应用该方法证明不等式举例。

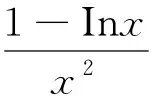
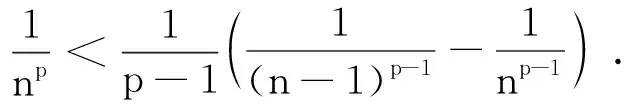
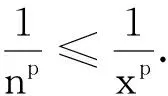
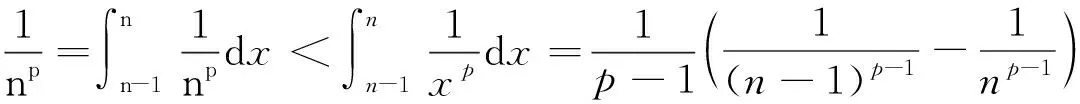
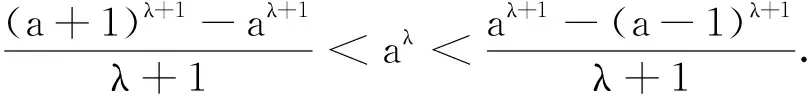
证明 1)当x∈[a,a+1] 时，由于a>1,-1<λ< 0,因此，有xλ≤aλ(仅当x=a取等号),

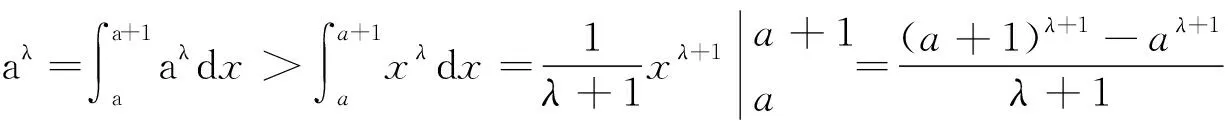
2)当x∈[a-1,a]时，由于a>1,-1<λ<0, 因此，有aλ≤xλ(仅当x=a取等号),

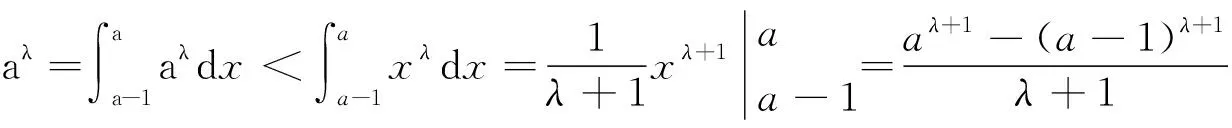
由(1)，(2)知，原不等式成立。

在参考文献[1]中，题3是用贝努利(Jac.Bernoulli)不等式证明的。

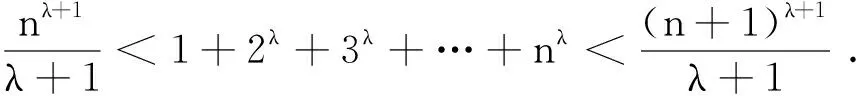
证明 当λ>0,x>0 时，函数f(x)=xλ是单调递增的，于是有

由此不等式，得

即原不等式得证。

……

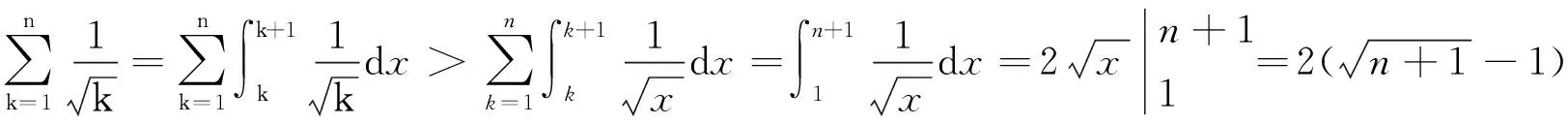
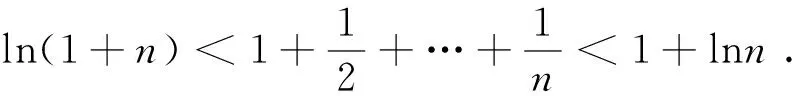
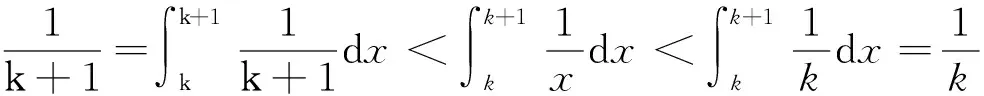
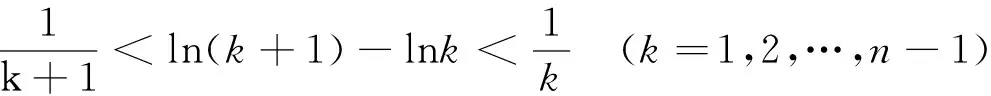
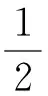
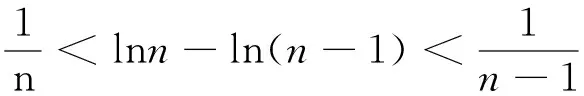
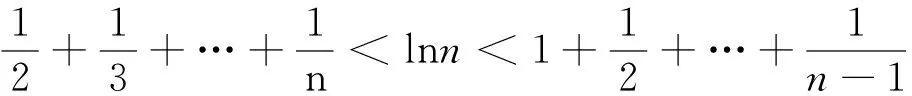
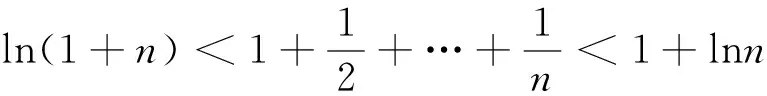
题7(2010年湖北省高考理科试卷第21题)

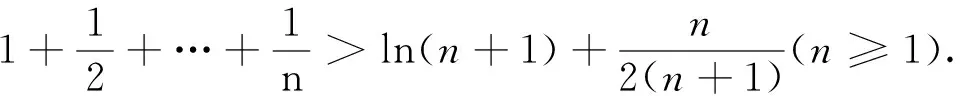
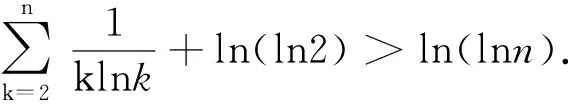
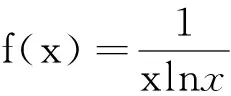
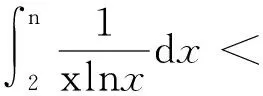
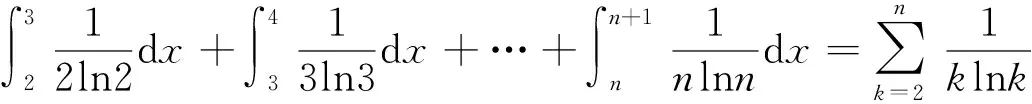
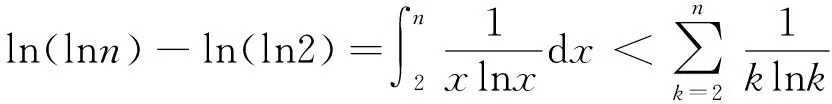
原不等式得证。

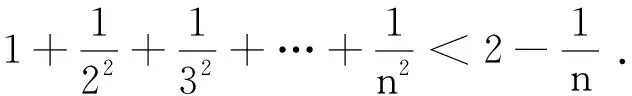
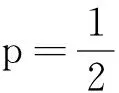
利用定积分在证明初等不等式时，可得到加强的不等式。

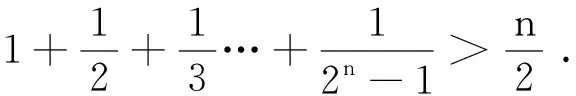
原证明用数学归纳法，当n=k+1 时，

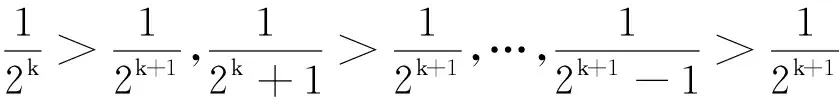
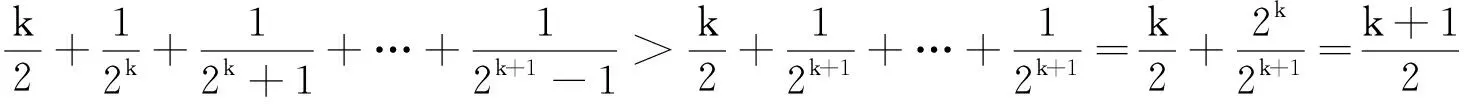
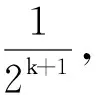
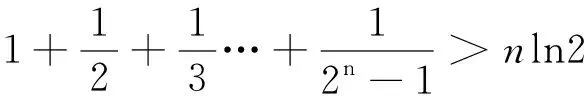
参考文献：

[1]余元希,田万海,毛宏德.初等代数研究下册[M].北京:高等教育出版社,1988.

[2]华东师范大学数学系.数学分析[M]. 北京:高等教育出版社,2001.

[3]人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心. 高中数学,选修4-5 不等式选讲[M]. 北京：人民教育出版社，2007.

[4]李盘喜，祝承亮，隋福林. 高中数学解题题典[M].长春：东北师范大学出版社，1998.