行准对称离散信道信道容量的计算

游雪肖，程 舰(湖北师范学院 数学与统计学院，湖北 黄石 435002)

信道是构成信息流通系统的重要部分，其任务是以信号形式传输和存储信息。信道容量是信道研究的核心，在物理信道一定的情况下，人们总希望传输的信息越多越好。信道容量表示了信道传输信息的最大能力。对于一般信道，信道容量的计算相当复杂。特殊信道如对称信道、准对称信道、信道矩阵可逆等的信道容量已经有了计算公式，而一般的信道容量通常需使用迭代算法求解，该方法比较繁琐，需使用计算机软件。本文在一般信道中定义了一种行准对称离散信道，该信道与准对称离散信道不同，准对称信道是列对称而行不对称，将其按列划分成对称矩阵，而行准对称信道是行对称而列不对称，将其按列划分成对称矩阵.本文还给出了该信道容量的计算方法，该方法可解决该类信道信道容量的计算。

1 预备知识

设离散信道的输入X∈{a1,a2,…,an}，相应的输出Y∈{b1,b2,…,bm}，信道统计特性由条件概率p(bj|ai)描述，将其称为信道转移概率.为直观起见，常用信道转移概率矩阵(简称信道矩阵)来描述信道特性.若行表示输入X，列表示输出Y，则信道矩阵为如下所示的n行m列的矩阵

定义1 离散无记忆信道容量定义为

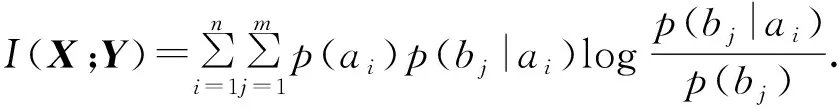
定义2 如果一个离散信源的信道矩阵行可排列而列不可排列，按列划分成若干个互不相交的子集，各子集既是行可排列也是列可排列，则称此矩阵所表示的信道为准对称信道.

定义3 如果一个离散信源的信道矩阵列可排列而行不可排列，按行划分成若干个互不相交的子集，各子集既是行可排列也是列可排列，则称此矩阵所表示的信道为按行划分的准对称信道，简称为行准对称离散信道.

引理 一般离散信道，当且仅当

I(ai;Y)=C，对所有ai其pi>0I(ai;Y)≤C,对所有ai其pi=0

时，I(X;Y)达到最大值，此时C为信道容量.其中

2 行准对称离散信道的信道容量的计算

定理 对于行准对称离散信道，当按行划分的每个子集的输入概率相等时可以达到信道容量.

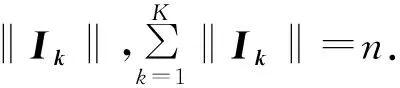
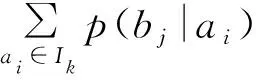
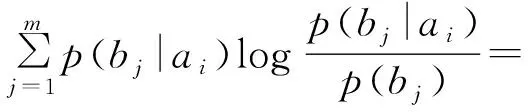
根据行准对称矩阵的定义可知，上式右端第一项与ai∈Ik无关，而第二项为常数，因此I(ai∈Ik;Y) 对所有ai∈Ik都相等，即这是一个与ai∈Ik无关的值，是一个常数.因而符合离散信道的信道容量定理，满足引理的条件，从而证得行准对称离散信道的信道容量当按行划分的每个子集的输入等概率时获得.

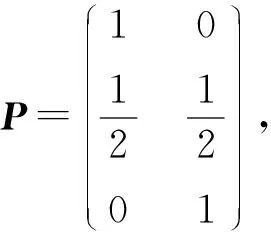
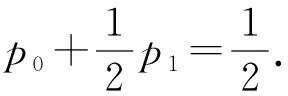
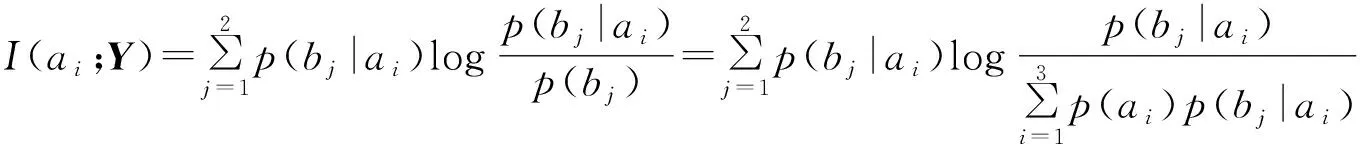
参考文献:

[1]陈 运.信息论与编码[M].北京：电子工业出版社，2009.

[2]傅祖芸，赵建中.信息论与编码[M].北京：电子工业出版社，2006.

[3]叶中行.信息论基础[M].北京：高等教育出版社，2003.