同心圆柱体间旋转气隙内对流换热的数值模拟研究

孙玉昕，赵旭峰，吴 波

（1 武汉工程大学 计算机科学与工程学院，湖北 武汉 430074；2 华中科技大学 能源与动力工程学院，湖北 武汉 430074；3 中国航空动力机械研究所，湖南 株洲 412000）

0 前言

发电机内部温度场的分布是保证发电机安全稳定持续运行的关键因素。如果温升过高，会导致绝缘的损坏，使绝缘的电气性能下降并引发电机内部的各种放电、短路故障，造成汽轮发电机结构上的损坏，最终导致汽轮发电机的故障，直接影响电站的可靠、经济运行[1]。定子和转子间环形气隙作为大型汽轮发电机运行过程中通风换热的重要组成部分，其内部流场的流动换热情况需要进行深入研究。

转子外壁和定子内壁分别形成了环形气隙的内、外壁面。由于发电机定子线圈和转子线圈的存在，环形气隙的内外壁表面并不是光滑的，而是形成了与线圈位置相对应的轴向凹槽。壁面上凹槽的存在使得环形气隙中的流动换热情况异常复杂。

流体在旋转同轴圆筒间的流动称为泰勒-库特流。泰勒-库特流因其独特的流动特性得到了越来越广泛的应用。例如，可以利用湍流泰勒涡流抑制膜污染和浓差极化现象来强化旋转管式微滤膜的分离过程；也可利用其径向混合性能来研制均混反应器；还可以深入认识高速机械的润滑液流动状态。除此之外，泰勒-库特流的径向流动特性可以强化流场的传热传质过程,减小壁面附近流体与主流体之间的温度和浓度差异[2]。因此，为研究汽轮发电机内环形气隙的流动换热特性，可以首先对定子、转子间环形气隙内流动的简化模型—泰勒-库特流模型进行研究，通过数值模拟的方法研究其流动换热规律，了解流场的分布对流动换热的影响，以增进对汽轮发电机冷却通流部分的了解，为其通流结构的优化设计和可靠运行提供依据。

国内外很多学者都对泰勒-库特流进行过研究。Taylor[3]在研究两独立同心旋转圆柱体间环形间隙内流动特性的过程中，用理论预测和实验验证了当内壁面转速达到临界转速时流场失稳，流体形成螺旋轨迹运动的现象。圆柱壁面转速较低时，流体沿壁面转动方向做简单的移动；当转速不断增大，达到临界转速后，流场失稳，流体就会形成细胞状微团并在流场中作螺旋轨迹运动，这种流动就称为泰勒-库特流，流场中形成的细胞状微团就是众所周知的泰勒涡。Wereley等[4]通过试验的方法研究了内圆柱转动外圆筒静止的环形间隙内泰勒库特流，Hwang等[5]通过数值计算的方法对文献[4]中的试验研究情况进行了模拟验证。R.Jakoby等[6]和I.Cornet等[7]通过试验研究了旋转圆筒泰勒涡的形成对内壁面换热的影响，并且得出了平均努赛尔数与旋转雷诺数的对应关系。国内有一些学者也对于泰勒-库特流的流动特性进行了研究，文献[2][8][9]中都是采用数值模拟的方法对流动特性进行的模拟和分析。

本文运用商用CFD软件对同心圆柱体间环形间隙内流体对流换热情况进行数值模拟，对流场中速度分布、温度分布、壁面热流密度分布以及不同泰勒数下流场的对流换热特性进行了讨论和分析，并对带凹槽环形气隙内的流动进行了模拟研究。

1 数值模型

1.1 物理模型及计算区域

几何模型的简图如1所示。其中，内圆柱面半径ri=43.4mm，外圆柱面半径ro=52.3mm，间隙高度d=ro-ri=8.9mm，内外半径比η=ri/r0=0.83，模型轴向长度L=356mm，轴向长度与间隙高度比Γ=L/d=40。

网格模型简图如图2所示。整个计算域采用结构化网格，并对局部进行加密。网格总数量为1,966,080，其中，径向、轴向和周向网格数量分别为 60、256、128。内外壁面均设置边界层网格，边界层网格均为10层，起始高度为0.005mm，增长比例为1.2。

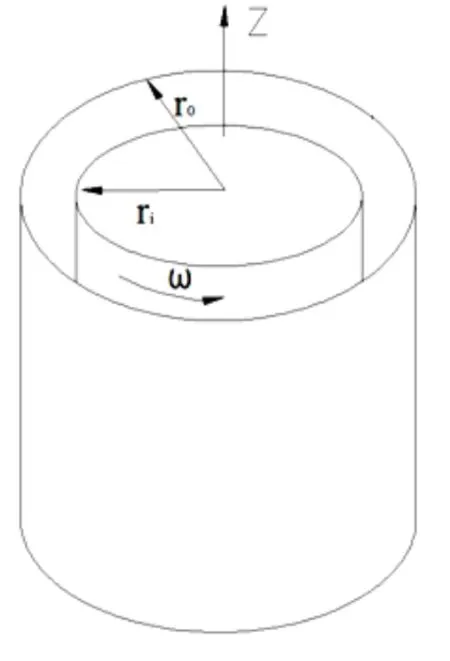
图1 几何模型

1.2 控制方程

应用Fluent6.3软件，采用三维不可压、稳态、层流模型。控制方程[10]：

（1）连续性方程：

（2）动量方程：

（3）能量方程：

对于湍流问题，还需要引入湍流模型，本文采用k-ε两方程模型[10]

（4）k-ε两方程模型：

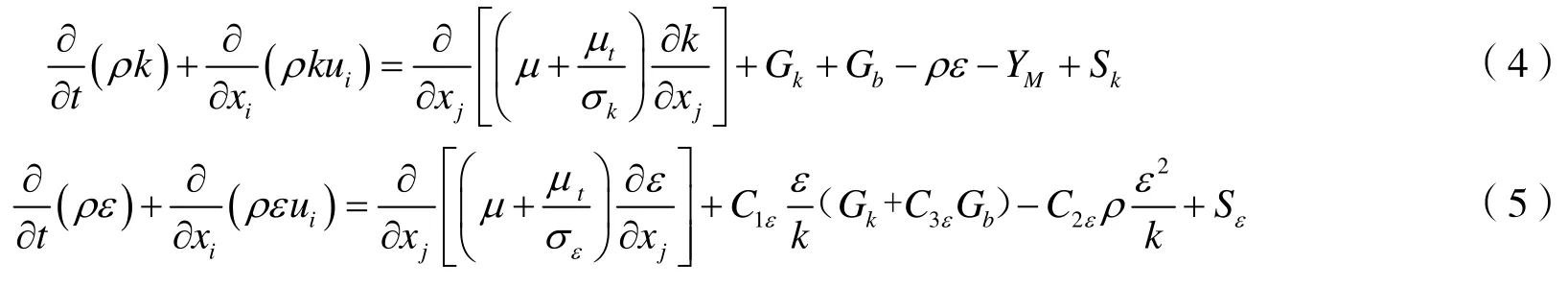
2 “泰勒-库特流”流动换热特性的求解和分析

2.1 物理条件及计算方法

计算模型内壁面温度设为343K，其转速设置详见表1，外壁面温度设为313K。介质为40℃空气（密度：1.128kg/m3(采用boussinesq假设)；比热容：1005 J/kg·K；热导率：0.0276w/m·K；运动粘性系数：1.913×10-5m2/s；热膨胀率(1/K)：0.00319；），没有轴向流动。

模型内外壁面间隙内的空气，在常物性和宏观能量守恒的假设条件下，其流动和能量传递满足连续性方程、动量方程和能量方程。速度压力耦合方法采用PISO算法，动量方程、能量方程以及湍流工况下的湍流耗散方程均采用二阶迎风格式。

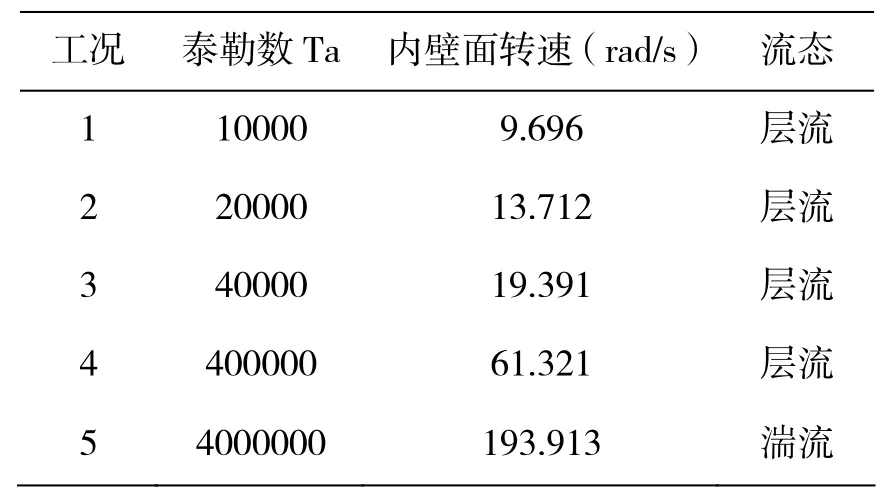
表1 工况设置

2.2 结果与分析

模拟计算按泰勒数Ta不同设置5个工况。其中，前四个工况中流场为层流状态，随着Ta的增大，到第5个工况时，流场为湍流状态。模型在工况1和工况5下得到的子午面上温度场分布云图如图3所示。

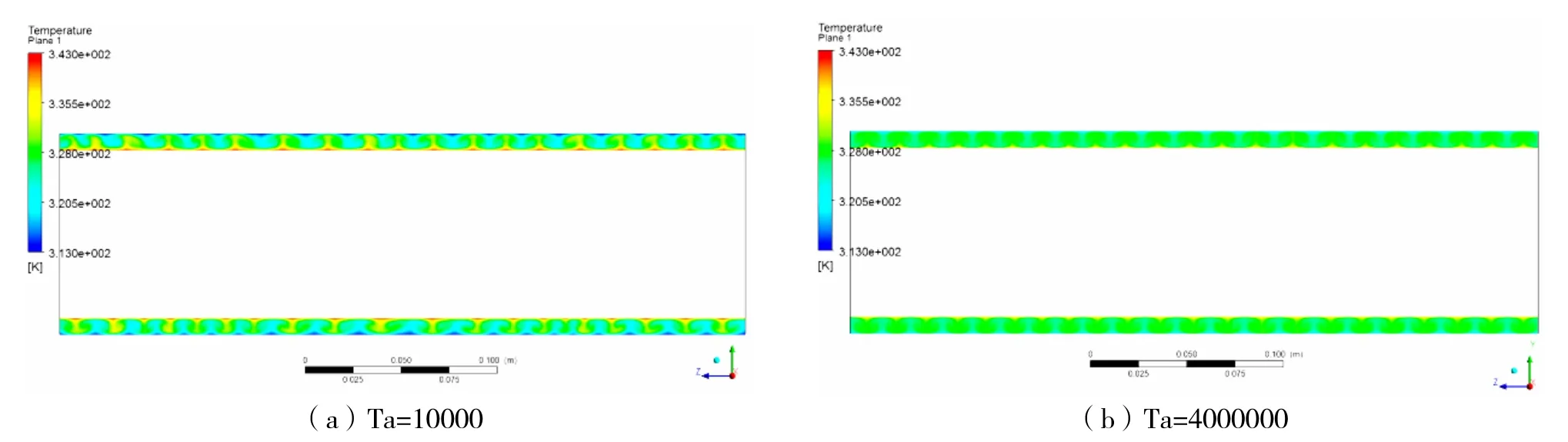
图3 不同工况下模型子午面温度云图

从子午面温度分布云图可以看出，由于模型内壁面转动在流场中形成的泰勒涡的作用，温度场也形成了类似“泰勒涡”的成对的涡团状温度分布。

以工况2（Ta=20000）的模拟结果为例，在模型中取一条沿轴向方向并经过内、外壁面间气隙中心的采样直线，取该直线上的速度与温度数据，以及内壁面上的热流密度沿轴向的分布数据。对比该采样直线上速度与温度沿轴向的分布如图。由图可以看出，速度、温度沿轴向的分布都呈现周期性的上下波动，波动频率与流场中泰勒涡的数量相同。同时，温度的波动与速度的波动趋势一致。沿模型轴向方向，每对涡的中心位置对应图中速度分布曲线的“波峰”位置，同时也对应温度分布曲线的“波峰”位置；相邻两涡的交界的位置对应速度分布曲线的“波谷”位置，同时也对应温度分布曲线的“波谷”位置。这说明，在每对涡中，中心位置处的速度最大，温度最高；在相邻两涡的交界的位置，速度最小，温度也最低。

对比采样直线上速度分布与内壁面热流密度沿轴向的分布如图 4。由图可以看出，内壁面热流密度沿轴向的分布也呈现周期性的上下波动，且波动频率与流场中泰勒涡的数量相同。不同的是，沿模型轴向方向热流密度的波动与速度波动的趋势完全相反。速度最大的位置，热流密度最小；速度最小的位置，热流密度最大。这是因为速度大的位置其温度也相对较高，流体与高温内壁面间温差较小，温度梯度较小，导致热流密度较小；相反，速度小的位置温度较低，流体与高温内壁面间温差较大，温度梯度也相对较大，因而使热流密度较大。综上所述，对于整个流场，其局部的换热强度沿轴向也呈现周期性的变化，在每对涡的中心处最小，沿轴向向两侧逐渐增加，到相邻泰勒涡的交界处达到最大，然后再逐渐减小，到涡的中心处达到最小。如同速度、温度的分布一样，往复交替变化。

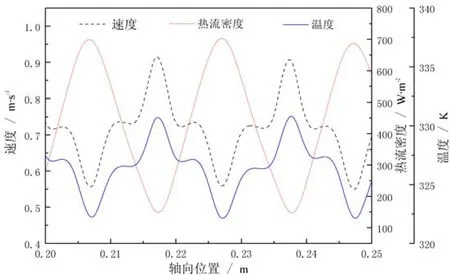
图4 Ta=20000的工况下速度、热流密度、温度轴向分布

由图5可以看出，各工况下局部对流换热系数的分布曲线与速度、温度、热流密度的分布曲线一样，沿轴向周期性波动，其波动趋势与速度分布和温度分布相反，与热流密度的分布相同，即在每对涡的中心处最小，在相邻两对涡的交界处最大。同时，从总体上看，泰勒数Ta越大（内壁面转速越高），平均对流换热系数就越大。从图中也可以看出，随着泰勒数Ta的增加，平均努赛尔数Nu也不断增加。也就是说，模型内壁面的转速越高，壁面与流体的对流换热强度越高，流体对壁面的冷却效果越好。

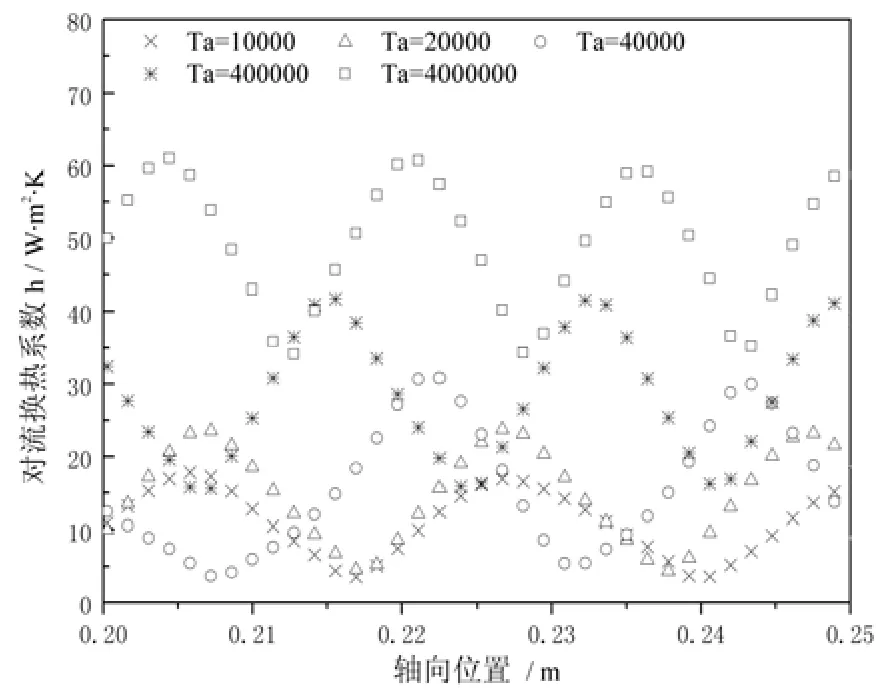
图5 各工况下局部对流换热系数沿轴向的分布曲线

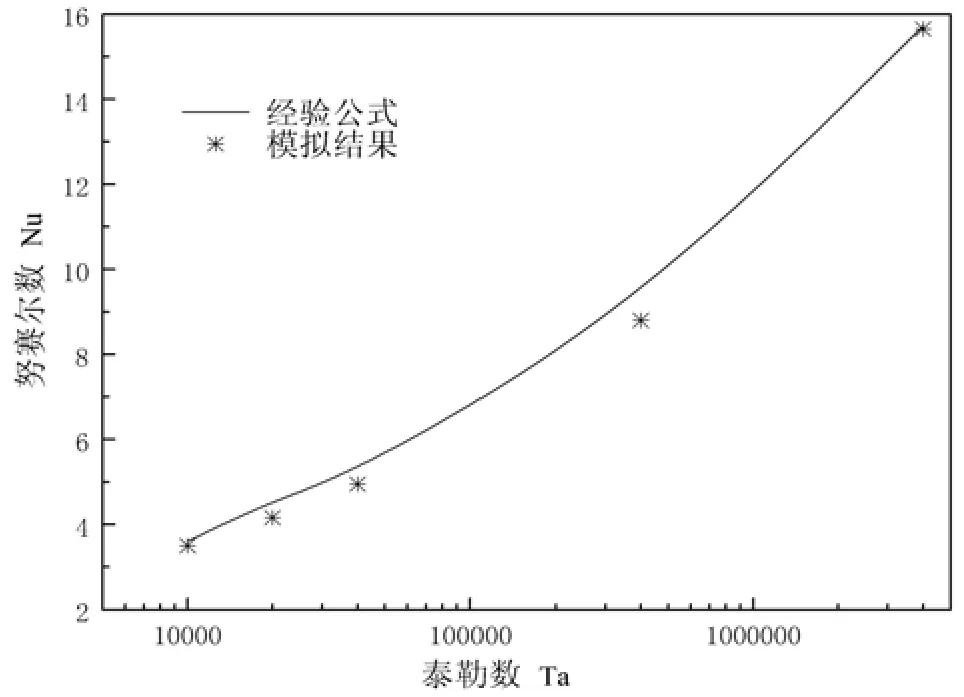
图6 数值计算Nu数与经验公式结果对比

I.S. Bjorklund和W.M. Kays[11]对环形气隙内流体在内壁面旋转情况下的对流换热特性进行了实验研究，并总结出计算该模型努赛尔数的经验公式：

本文所选数值计算模型的尺寸及泰勒数的设置均满足该经验公式的使用范围，将数值计算得出的努赛尔数与经验公式得出的努赛尔数对比，如图6。

由对比结果可以看出，数值计算的结果与文献中经验公式的最大偏差为9.88%，最小偏差为0.46%，平均偏差为4.50%，并且，模拟结果和经验公式得出的努赛尔数的变化趋势一致。这一结果证明了该数值计算的有效性。

3 带轴向凹槽气隙模型的流动模拟

为使环形气隙模型更加接近真实情况，参照Alstom公司制造的某型号发电机的结构特点，建立带轴向凹槽气隙模型，对气隙内流动情况进行模拟。为减少计算时间，提高计算效率，根据环形气隙周期性对称的结构特点，取整个环形气隙的1/56作为计算域以减少网格数量，计算域网格分布如图7所示，整个计算域同样采用结构化网格，并对局部进行加密，网格总数量为 2,662,214。模型内壁面转速为 377rad/s（3600r/min），介质采用理想气体。

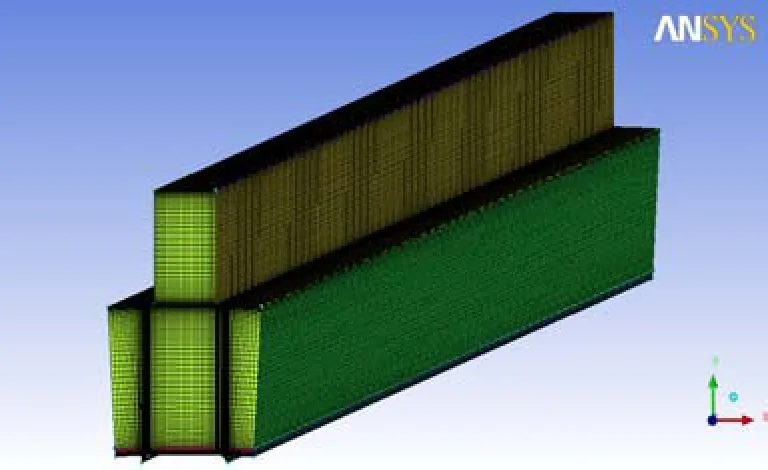
图7 带轴向凹槽气隙模型网格分布

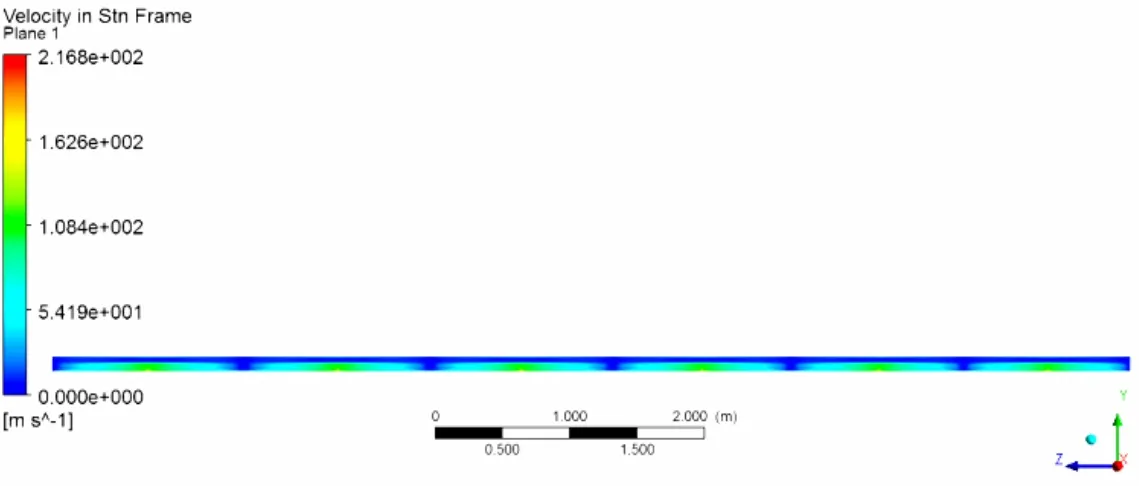
图8 带轴向凹槽气隙模型子午面速度云图

计算得到模型子午面的速度分布如图8所示。可以看出，由于环形气隙内外壁面上凹槽的存在，极大的增加了壁面对流场的扰动作用，气隙内的流动更加混乱，使得流场中涡的数量减少，尺度增大。由光滑壁面模型的流动换热计算可知，流场中温度和热流密度的分布受速度分布的影响很大，可以推测，壁面凹槽在影响速度分布的同时，也影响了温度以及热流密度的分布。

分别在距离内壁面 5mm（R=0.58m）和气隙中部（R=0.6065m）各取一条沿轴向方向的采样直线，提取采样直线上的径向分速度数据，如图9所示。由该图可以看出，沿模型轴向方向，流场的径向分速度呈正负交替变化的趋势。在内壁面附近（R=0.58），正向速度的峰值略大于负向速度的峰值，但二者差距不大；在气隙中部主流区域（R=0.6065m），正向速度的峰值要明显大于负向速度的峰值。而泰勒涡的形成也正是由于流场中的这种方向相反的径向流动间隔作用的结果。由于流场中的这种较强的径向流动，使得内壁面附近的流体能够更多的流到外壁面附近，从而强化了流场的传热传质过程。

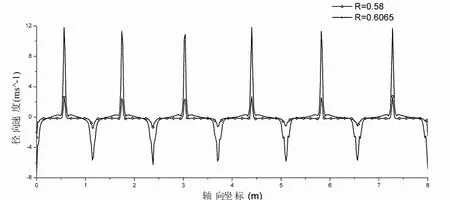
图9 带轴向凹槽气隙模型径向速度的分布

4 结论

（1）内壁面的转动在流场中形成的泰勒涡改变了流体内温度场的分布，使温度场也形成了类似“泰勒涡”的成对的涡团状分布；

（2）温度场沿轴向的周期性波动，使内壁面的热流密度沿轴向方向也产生了周期性波动，在涡的中心位置，热流密度最小，对流换热系数最小，该位置对流换热的能力最差；在相邻两对涡的交界处，热流密度最大，对流换热系数最大，该位置对流换热的能力最好；

（3）内壁面转速越大，平均努赛尔数Nu越大，流场的对流换热性能越好，流体对壁面的冷却效果就越好；

（4）环形气隙壁面增加凹槽后，壁面对流场扰动作用的增强使得流场中速度的分布发生了显著的变化；可以推测，这种扰动也会使温度和热流密度的分布发生变化，凹槽的存在对流场换热性能的影响会在后续的工作中进行深入研究；

（5）气隙内的泰勒-库特流在流场形成了明显径向流动，这种径向流动强化了发电机环形气息内的传热传质过程；

由于大型汽轮发电机定子内壁面和转子外壁面结构特殊，内外壁面间气隙内真实的流动换热情况更加复杂，本文的工作仅是对该问题从数值模拟的角度开展前期的基础研究，为了解其实际的运行状况，提高发电机运行的安全性和稳定性，还需要进一步的研究和探索。

[1]丁树业. 大型发电机定子复杂结构内流体流动与传热特性的研究[D]. 哈尔滨：哈尔滨理工大学，2008.6.

[2]周先桃，潘家祯，陈理清，等. 湍流泰勒涡特性的数值模拟[J]. 华东理工大学学报(自然科学版), 2006， 32（5）:617-622.

[3]Taylor GI. Stability of a viscous liquid contained between two rotating cylinders[J]. Phil Trans R Soc, 1923, A223:289-343.

[4]Steven T. Wereley, Richard M. Lueptow, Velocity field for Taylor-Couette flow with an axial flow[J]. J. PHYSICS OF FLUIDS, 11(12).

[5]Jong-Yeon Hwang, Kyung-Soo Yang, Numerical study of Taylor-Couette flow with an axial flow[J]. J. Computers ＆ Fluids,2004,33: 97-118.

[6]R. Jakoby, S. Kim, S. Wittig. Correlations of the convection heat transfer in annular channels with rotating inner cylinder[J].ASME J. Eng. Gas Turbines Power, 1991, 21: 670-677.

[7]I. Cornet, R. Greif, J.T. Teng, F. Roehler, Mass transfer to rotating robs and plates[J]. International Journal of Heat Mass Transfer ,1980,23: 805-811.

[8]王宇，徐忠锋. 同轴圆柱间旋转流动Taylor-Couette流的数值模拟[J]. 渤海大学学报(自然科学版)，2004, 25(3):249-251.

[9]刘难生，董宇红，陆夕云，等. 旋转同心圆筒间 Couette-Taylor流动的数值模拟[J]. 中国科学技术大学学报，2002,32(1):91-97.

[10]陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001.

[11]I.S. Bjorklund, W.M. Kays, Heat transfer between concentric rotating cylinders[J]. Journal of Heat Transfer, 1959, 81: 175-186.