关于二阶线性微分方程解的增长性
宫 娟,陈宗煊
(华南师范大学数学科学学院,广东广州 510631)
关于二阶线性微分方程解的增长性
宫 娟,陈宗煊*
(华南师范大学数学科学学院,广东广州 510631)
研究了二阶微分方程f″+A1(z)P(ez)f′+A0(z)Q(ez)f=0和f″+(A1(z)P(ez)+D1(z))f′+(A0(z)Q(ez)+D0(z))f=0解的增长性,其中P(ez)与Q(ez)是ez的非常数多项式,它们的常数项都为零,且次数不相等.证明了该方程的每个非零解有无穷级.
微分方程; 整函数; 增长级
1 引言与结果
本文所涉及的亚纯函数的值分布的基本理论和标准记号见文献[1]-[3], 并用σ(f)表示亚纯函数f(z)的增长级.
考虑微分方程
f″+e-zf′+Q(z)f=0
(1)
解的增长级问题,其中Q(z)是有限级整函数.
众所周知,方程(1)的每个解都是整函数,而且如果f1和f2是方程(1)的任意2个线性无关解,那么至少有一个具有无穷级[4],所以方程(1)的“大多数”解具有无穷级.
一个很自然的问题是:当Q(z)满足什么条件时,能保证方程(1)的每个解具有无穷级?
文献[5]证明了
定理A 假设C(≠0)是复常数,如果方程
f″+e-zf′+Cf=0
(2)
具有有限级非零解,那么C=-k2,其中k是一个正整数,反过来,对每个正整数k,方程(2) (其中C=-k2)具有关于ez的k次多项式解f.
文献[6]-[8]研究了Q(z)是特殊多项式的情况,文献[9]对于Q(z)是一般多项式的情况证明了
定理B[9]假设Q(z)是非常数多项式,D是非零常数,那么方程
f″+De-zf′+Q(z)f=0
(3)
的所有非零解具有无穷级.
对于Q(z)是超越整函数的情况,有
定理C[8]假设Q(z)是超越整函数且级σ(Q)≠1,那么方程(1)的每个非零解具有无穷级.
定理C表明当σ(Q)=1时,方程(1)可能有有限级解,继续深入考虑这个问题:当σ(Q)=1时,满足什么条件,将保证方程(1)的每个非零解有无穷级?对于更一般的问题,有
定理D[10]假设Aj(z) (≢0;j=0,1)是整函数,且σ(Aj)<1,a,b是复常数,满足ab≠0和a=cb(c>1),那么方程
f″+A1(z)eazf′+A0(z)ebzf=0
(4)
的所有非零解具有无穷级.
定理E[10]假设Aj(z) (≢0),Dj(z)(j=0,1)是整函数,且σ(Aj)<1,σ(Dj)<1,a,b是复常数,满足ab≠0和arga≠argb或a=cb(0 f″+(A1eaz+D1)f′+(A0ebz+D0)f=0 (5) 的每个非零解具有无穷级. 定理D和定理E大大推广和完善了文献[6]-[9]的结果. 定理1 假设P(ez)=amemz+am-1e(m-1)z+…+a1ez,Q(ez)=bnenz+bn-1e(n-1)z+…+b1ez,其中aj(j=1,…,m),bk(k=1,…,n)是常数,且ambn≠0,m,n≥1,m>n,Aj(z) (≢0;j=0,1)是整函数,且σ(Aj)<1.那么方程 f″+A1(z)P(ez)f′+A0(z)Q(ez)f=0 (6) 的所有非零解具有无穷级. 定理2 假设P(ez)=amemz+am-1e(m-1)z+…+a1ez,Q(ez)=bnenz+bn-1e(n-1)z+…+b1ez,其中aj(j=1,…,m),bk(k=1,…,n)是常数,且ambn≠0,m,n≥1,m f″+(A1P(ez)+D1)f′+(A0Q(ez)+D0)f=0 (7) 的每个非零解具有无穷级. 从定理1和定理2推导下面的推论: 本文通过对硅质岩主量元素、微量元素和稀土元素的研究,分析该区硅质岩的沉积环境及其与成矿作用的关系,对把握正确的找矿方向具有重要意义。 推论1 假设P(ez)=amemz+am-1e(m-1)z+…+a1ez,Q(ez)=bnenz+bn-1e(n-1)z+…+b1ez,其中aj(j=1,…,m),bk(k=1,…,n)是常数,且ambn≠0(m,n≥1),Aj(z) (≢0;j=0,1)是整函数,且σ(Aj)<1.若m≠n, 则方程(6)的所有非零解有无穷级. 注1 假设P(ez)=amemz+am-1e(m-1)z+…+a1ez,其中am,…,a1是常数,m≥1是整数,am≠0,由上面P(ez)的定义,能得到 |P(ez)|=|am|emrcos θ(1+o(1)) 其中M(>0)是某常数. 引理1[10]假设P(z)=(α+iβ)zn+… (α,β是实数,|α|+|β|≠0) 是多项式且次数n≥1,A(z)(≢ 0)是整函数且σ(A) (i)如果δ(P,θ)>0, 那么 exp{(1-ε)δ(P,θ)rn}<|g(reiθ)|< exp{(1+ε)δ(P,θ)rn}, (8) (ii)如果δ(P,θ)<0, 那么 exp{(1+ε)δ(P,θ)rn}<|g(reiθ)|< exp{(1-ε)δ(P,θ)rn}, (9) 由引理1和注1容易得到下面的引理2. (i)如果cosθ>0,那么 exp{(1-ε)mrcosθ}(1+o(1))≤|g(reiθ)|≤ exp{(1+ε)mrcosθ}(1+o(1)), (10) (ii)如果cosθ<0,那么 |g(reiθ)|≤Rexp{rcosθ+rσ(A)+ε}, (11) 引理3[11]设f(z) 是整函数,|f(k)(z)|在某射线argz=θ上是无界的,那么存在一无穷点列zn=rneiθ(n=1,2,…), 其中rn→∞,满足f(k)(zn)→∞和 (12) 引理4[12]假设f是超越亚纯函数且σ(f)=σ<∞,H={(k1,j1), (k2,j2),…, (kq,jq)}是一个不同整数对的有限集,且满足ki>ji≥0 (i= 1,2,…,q), 假设ε>0是一任意给定常数,那么存在一线测度为零的集合E⊂[0,2), 满足:若ψ[0,2)E, 则存在常数R0=R0(ψ)>1, 满足对所有满足argz=ψ和|z|≥R0的z,对所有(k,j)H,有 (13) 引理5[13]假设f(z)是一整函数且σ(f)=σ<∞,假设存在子集E⊂[0,2)具有线测度零,满足对任意射线argz=θ0[0,2)E, |f(reiθ0)|≤Mrk, 其中M=M(θ0)>0是一常数,k(>0)是一与θ0无关的常数,则f(z)是一多项式且degf≤k. 假设f(z)(≢0)是式(6)的超越解且σ(f)=σ<∞.由引理4和注2可知,对任给ε>0,满足 (14) (15) (i)如果cosθ<0,那么 |A1(reiθ)P(ereiθ)|≤Nexp{rcosθ+rσ1+ε}, |A0(reiθ)Q(ereiθ)|≤Nexp{rcosθ+rσ0+ε}; (16) (ii) 如果cosθ>0,那么 |A1(reiθ)P(ereiθ)|≥exp{(1-ε)mrcosθ}(1+o(1)), |A0(reiθ)Q(ereiθ)|≤exp{(1+ε)nrcosθ}(1+o(1)); (17) 其中N>0是常数,σ1=σ(A1),σ0=σ(A0). 情形1 cosθ<0.由式(6),得到 (18) 如果|f″(reiθ)|在射线argz=θ上是无界的,那么由引理3,存在一无穷点列{zt=rteiθ},其中rt→∞满足f″(zt)→∞和 (19) 将式(16)和(19)代入式(18),得到: 当t→∞时, 这是一个矛盾.所以 |f″(reiθ)|≤M1 (20) 在argz=θ上成立,其中M1>0是常数.取积分路线Γ={s: args=θ,0≤|s|≤|z|}, 由式(20)和 得到 |f′(z)|≤M2|z|, (21) 其中M2>0是常数.类似地,由式(21)得到在射线argz=θ上,|f(z)|≤M|z|2(M>0是常数). 情形2 cosθ>0.由式(6),得到 (22) 如果|f′(reiθ)|在射线argz=θ上是无界的,那么由引理3,存在一无穷点列{zt=rteiθ},其中rt→∞满足f′(zt)→∞和 (23) 将式(15)、(17)、(23)代入式(22),得到: 当rt→∞时, exp{(1-ε)mrtcosθ}(1+o(1))≤ nrtcosθ}(1+o(1)), (24) 由式(14)、(24),得到 (25) 由于cosθ>0,可知当rt→∞,式(25)是一个矛盾.所以在射线argz=θ上 |f′(reiθ)|≤M (26) 成立.使用如同上面相同的理由,得到在射线argz=θ上|f(z)|≤M|z|2成立. exp{(1-ε)mrcosθ}rk-1(1+o(1))≤ |A1(reiθ)P(ereiθ)f′(reiθ)|≤ |f″(reiθ)|+|A0(reiθ)Q(ereiθ)f(reiθ)|≤ r2kexp{(1+ε)nrcosθ}(1+o(1)), 由Q(ez)≢0,可知f不可能为非零常数.所以式(6)的每个非零解具有无穷级. 使用类似定理1的证明方法,可以证明式(7)不可能有非零多项式解. 下面假设f(z)(≢0)是式(7)的超越解且σ(f)=σ<∞.由引理4,对任给ε(0<2ε<1-σ(D1)),存在集合E1⊂[0,2)有线测度零,如果θ[0,2)E1,那么存在常数R0=R0(θ)>1,使得对所有满足argz=θ和|z|=r≥R0的z, (27) |A0(reiθ)Q(ereiθ)+D0(reiθ)|≥ exp{(1-ε)nrcosθ}(1+o(1)), (28) |A1(reiθ)P(ereiθ)+D1(reiθ)|≤ exp{(1+ε)mrcosθ}(1+o(1)). (29) 由式(7)、(27)、(28)、(29)得到 exp{(1-ε)nrcosθ}(1+o(1))≤|A0Q(ez)+D0|≤ 2r2(σ-1+ε)exp{(1+ε)mrcosθ}(1+o(1)). (30) exp{(m+n)εrcosθ}≤4r2(σ-1+ε). 这是一个矛盾,定理2证毕. [1] HAYMAN W. Meromorphic functions[M].Oxford: Cl-arendon Press, 1964. [2] 杨乐. 值分布论及其新研究[M]. 北京: 科学出版社, 1982. [3] LAINE I. Nevanlinna theory and complex differential equations[M]. Berlin: W de Gruyter, 1993. [4] HILLE E. Ordinary differential equations in the complex domain[M].New York: Wiley,1976. [5] FREI M. Uber die subnormalen losungen der differentialgleichungw″+e-zw′+(konst.)w=0[J]. Comment Math Helv, 1962, 36: 1-8. [6] OZAWA M. On a solution ofw″+e-zw′+(az+b)w=0[J]. Kodai Manth, 1980, 3: 295-309. [7] AMEMIYA I, OZAWA M. Non-existence of finite order solutions ofw″+e-zw′+Q(z)w=0[J]. Hokkaido Math, 1981, 10: 1-17. [8] GUNDERSEN G. On the question of whetherf″+e-zf′+B(z)f=0 can admit a solutionf≢0 of finite order[J]. Proc RSE, 1986, 102A:9-17. [9] LANGLEY J K. On complex oscillation and a problem of Ozawa[J]. Kodai Math, 1986, 9:430-439. [10] 陈宗煊. 微分方程f″+e-zf′+Q(z)f=0解的增长性[J]. 中国科学:A 辑, 2001, 31(9): 775-784. [11] GUNDERSEN G. Finite order solutions of second order linear differential equations[J]. Trans Amer Math Soc, 1988, 305: 415-429. [12] GUNDERSEN G. Estimates for the logarithmic derivative of a meromorphic function, plus similar estimates[J]. London Math Soc, 1988, 37 (2): 88-104. [13] CHEN Zongxuan. On the growth of solutions of a class of higher order differential equations[J]. Chin Ann of Math, 2003,24B(4): 501-508. Keywords: differential equation; entire function; order of growth OntheGrowthofSolutionsofSecondOrderLinearDifferentialEquations GONG Juan, CHEN Zongxuan* (School of Mathematics,South China Normal University,Guangzhou 510631,China) The growth of solutions of the differential equationsf″+A1(z)P(ez)f′+A0(z)Q(ez)f=0 andf″+(A1P(ez)+D1(z))f′+(A0Q(ez)+D0(z))f=0 is investigated, whereP(ez)andQ(ez)are nonconstant polynomials without constant term, and degPis not equal to degQ. It is showed that the order of growth of each nonzero solution of the above equations is infinite. 2010-12-10 国家自然科学基金项目(10871076) *通讯作者,chzx@vip.sina.com 1000-5463(2012)01-0029-04 O175.29 A 【责任编辑 庄晓琼】2 引理和注




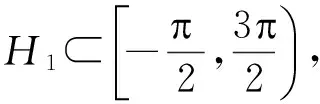
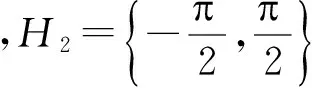


3 定理1 的证明

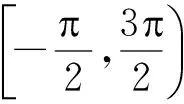
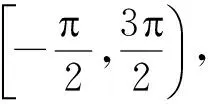

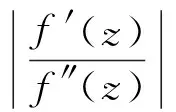
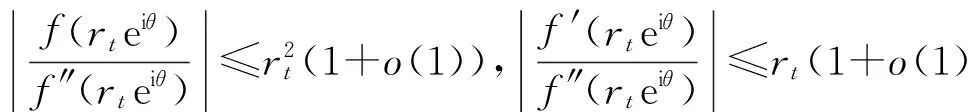
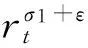
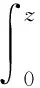
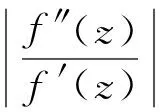
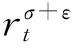
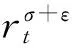


4 定理2 的证明