基于图像灰度点特征提取算子的比较研究及改进*

王启春 郭广礼 查剑锋 刘 神

(1)中国矿业大学国土环境与灾害监测国家测绘局重点实验室，徐州 221116 2)中国矿业大学江苏省资源环境信息工程重点实验室，徐州 221116 3)中国矿业大学环境与测绘学院，徐州221116)

基于图像灰度点特征提取算子的比较研究及改进*

王启春1，2，3)郭广礼1，2，3)查剑锋1，2，3)刘 神3)

(1)中国矿业大学国土环境与灾害监测国家测绘局重点实验室，徐州 221116 2)中国矿业大学江苏省资源环境信息工程重点实验室，徐州 221116 3)中国矿业大学环境与测绘学院，徐州221116)

现阶段常用的基于图像灰度的点特征算子有Moravec算子、Harris算子、Forstner算子和Forstner改进算子，不同算子的提取速度、定位准确性、稳定性存在一定的差异。通过人造测试影像和真实拍摄影像测评各算子的提取速度、定位准确性、稳定性、参数自适性，比较得出各算子的优缺点，并在此基础上提出一种改进算子。研究结果表明:改进算子具有稳定性强、定位精度高和自动设置阈值的特点。

点特征提取;Moravec算子;Harris算子;Forstner算子;改进算子

1 引言

特征提取是影像分析和影像匹配的基础，也是单张影像处理的最重要任务，广泛应用于图像的识别、分割、配准、拼接等各方面，因此具有重要的意义。特征提取算子可分为点特征提取算子与线特征提取算子。现阶段点特征提取算子发展比较成熟，并易于程序实现，在数字影像提取工作中得到了广泛的应用［1］。目前点特征提取算子大致可分为两类:基于模板匹配的方法和基于几何特征的方法。基于模板匹配的方法(如SUSAN算子)计算耗时长，不适用于大量特征点的提取［2］，所以在数字摄影测量中运用得较少。基于几何特征的方法又主要分为两类:基于图像边缘的方法和基于图像灰度的方法。基于图像边缘的方法往往需要对图像边缘进行编码，这在很大程度上依赖于图像的分割和边缘提取，具有相当大的难度和计算量;基于图像灰度的方法是通过计算点的曲率及梯度来检测点，避免了对图像边缘进行编码的缺陷，是目前数字摄影测量研究的重点［3］。

现阶段常用的基于图像灰度的点特征提取算子有Moravec算子、Harris算子、Forstner算子和Forstner改进算子等，目前对它们的系统性的比较研究较少，如余晨等人［2］的基于灰度信号的点特征提取方法比较研究缺少对几种算子稳定性的比较，张春美等人［4］的几种特征点提取算法的性能评估及改进缺少对几种算子参数自适性的比较，因此非常有必要对几种算子作一个系统性的比较研究。本文通过人造测试影像和真实拍摄影像综合测评各算子的性能得出了各算子的优缺点，在此基础上提出基于Forstner算子加权中心化的Harris改进算子，提高了Harris算子的定位精度，并通过区域特征点兴趣值的均值作为阈值的方法，实现了兴趣值阈值的自动检测，提高了特征点的提取效率。

2 点特征提取算子

根据算法原理的不同，基于图像灰度的点特征提取方法可分为两类:一是基于图像梯度的点特征提取方法，如Moravec算子、Forstner算子，描述局部灰度信号的变化情况，对各类特征点均有响应，因此广泛应用于航空摄影测量中的点特征提取;二是基于图像的亮度对比关系的点特征提取方法，如基于灰度自相关函数的Harris算子。由于Forstner算子的计算较复杂，张祖勋等人［1］对其进行了改进，本文中的Forstner改进算子是根据该方法实现的。

在数字摄影测量中最佳的点特征算子提取出的特征点应满足［5］:

1)确定性:一个好的特征点应该与背景有明显的区别，并且在局部领域中是唯一的;

2)不变性:特征点的选择及其位置的确定，对于可能存在的几何和辐射畸变应该是不变的，不变性的程度直接影响到基于点特征匹配的精度和可靠性;

3)稳定性:所选的特征点应该在另一张影像上出现，因此特征点的筛选应该具有稳定性，对于噪声和粗差不敏感;

4)唯一性:确定性保证特征点能够区别于局部范围的其他点。除了局部确定性外，特征点还应该具有某种程度上的整体唯一性;

5)可理解性:特征点应该有明显的意义，以使得特征点便于用于相关分析和更高级的影像解译。

对于实时匹配来说，点特征算子的提取速度是一个重要的指标。在点特征提取时不应提取平坦区域的点作为特征点，并要保证特征点的唯一性，本文将特征点的确定性和唯一性概括为定位准确性，所以定位准确性也是点特征算子评估的重要指标。在近景摄影测量中，连续拍摄的立体像对受旋转角、对比度和噪声的影响较大，为了较好点特征匹配需要在立体像对中提取相同的特征点，因此评估点特征算子的稳定性显得更加重要。各算子提取的结果跟各自参数选择有关，评估各算子的参数自适性，有利于各算子自动设置参数的研究。

3 点特征提取算子测试的结果分析

通过一幅包括多种类型角点的人造测试影像(图1)和一幅真实拍摄的影像(图2)综合测评各算子的提取速度、定位准确性、稳定性、参数自适性等。

4种点特征提取算子对人造测试影像的测试结果如图1所示，其中图1(a)为Moravec算子的测试结果，其阈值T=10 000;图1(b)为Harris算子的测试结果，其阈值T=10 000，k=0.05，d=0.5;图1 (c)为Forstner算子的测试结果，其中Tq=0.7，f= 1;图1(d)为Forstner改进算子的测试结果，其阈值T=20，Tq=0.5。

4种点特征提取算子对真实拍摄影像的测试结果如图2所示，其中图2(a)为Moravec算子的测试结果，其阈值T=20 000;图2(b)为Harris算子的测试结果，其阈值T=100 000，k=0.05，d=0.5;图2 (c)为Forstner算子的测试结果，其中Tq=0.6，f= 0.8;图2(d)为Forstner改进算子的测试结果，其阈值T=30，Tq=0.4。

3.1 提取速度测试

实时运算中时间的节约至关重要，所以评价一种算子时提取速度是一个重要的性能，本文通过如图1(分辨率为256×256)和图2(分辨率为225× 231)两幅影像进行测试，用4种算子提取了遥感特征点的平均时间，其测试结果如表1所示。其中测试的软件为Matlab 7.1，测试的计算机处理器为Genuine Intel(R)，主频1.8 GHZ，内存1G。

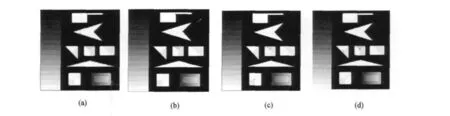
图1 4种点特征算子对人造测试影像的测试结果Fig.1 Test results by use of four kinds of interest point detect operators to the artificial test image

图2 4种点特征算子对真实拍摄影像的测试结果Fig.2 Test results by use of four kinds of interest point detect operators to the really taken image

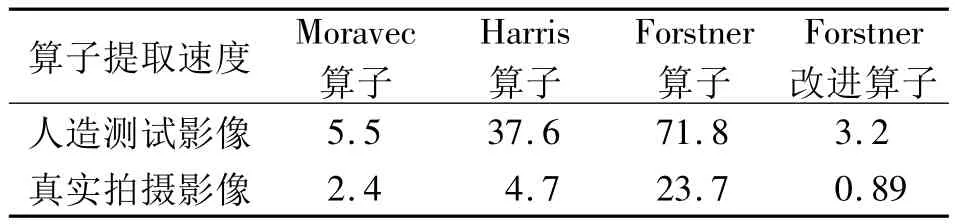
表1 4种点特征提取算子的提取速度比较(单位：毫秒)Tab.1 Comparison among speeds of four kinds of interest point detect operators(unit：ms)

由表1可得:Forstner改进算子的提取速度最快，而Forstner算子的提取速度最慢。由于Forstner算子较复杂，所以其提取速度较慢;Moravec角点提取算子是一个相对简单的算子，它最显著的优点是实现简单快速，所以其提取速度也相对较快。Forstner改进算子其最大的改进就是计算速度变快，不但比Forstner算子快，甚至要比Moravec算子更快。

3.2 定位准确性测试

定位准确性是判断提取的特征点位置是否接近正确的角点位置及判断角点的定位精度［6］。本文将人造测试影像裁减部分角点作为定位准确性测试影像(图3)。该测试影像中的10个角点利用Matlab 7.1中的Date cursor工具确定其准确位置，以正左上方的角点为起点，顺时针得出各角点的坐标为(31，15)、(226，15)、(226，24)、(127，24)、(127，74)、(224，76)、(170，132)、(224，187)、(42，131)、(31，75)。角点定位的精度主要以提取的特征点坐标与响应的已知特征点坐标之间的整体均方根误差δ、行方向均方根误差δx和列方向均方根误差δy3个量来判断。设(xi，yi)为实际提取特征点的坐标，(Xi，Yi)为已知特征点坐标。以下是计算3个量的公式:

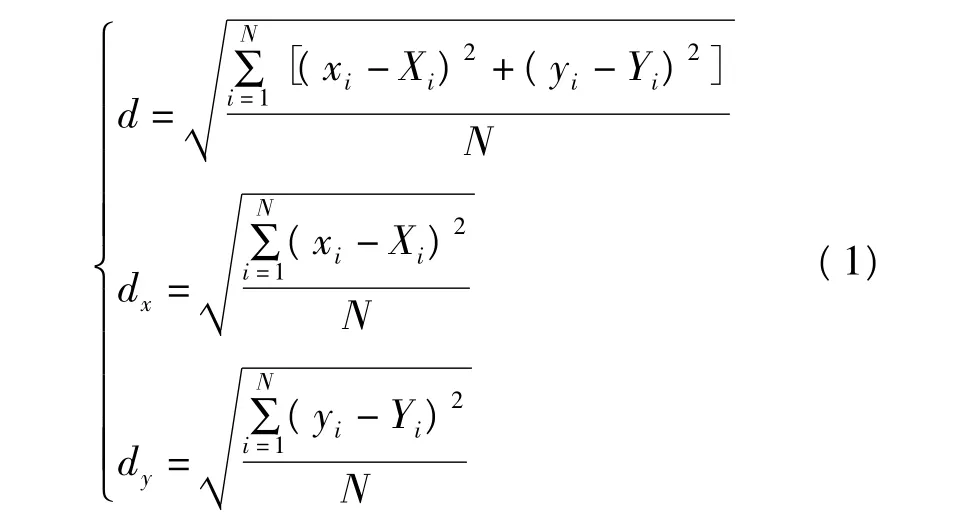
图3 定位准确性测试影像Fig.3 Accuracy test image

由表2可得，Forstner算子和Forstner改进算子的提取精度都较高，其定位精度达到了亚像素级; Harris算子提取特征点的精度其次，Moravec算子提取特征点的精度最差。分析其主要原因:Forstner算子采用了微分加权的方法对特征点进行精确定位，在理想情况下，其理论精度可达0.6个像素;而Harris算子只能在单一尺度下进行检测，尺度的选择影响特征点的定位精度，所以使其定位精度一般;由于Moravec算子的算法较简单，只考虑了45°方向的平移，并导致其角点响应不是各方向同性的(如图1 (a)所示)，所以对斜线边缘的反应很强，导致其定位精度较低。

表2 4种点特征提取算子的精度比较Tab.2 Comparison of accuracy of four kinds of interest point detect operators

3.3 稳定性测试

稳定性主要判断提取的特征点对影像的旋转变化、对比度变化和噪声影响的反应程度，而反应程度与提取特征点的重复度率有关，所以测试算子的稳定性即是检测算子提取特征点的重复率，重复率越高的算子稳定性越好。本文以真实拍摄的影像作为稳定性测试影像，并以图2中各算子提取的特征点为基础，分别测试各算子的旋转变化、对比度变化、噪声影响的重复率，其中重复率即是影像经变化后提取的特征点坐标与图2中对应算子提取的特征点坐标之间的误差在限定范围之内(一般为1.5 pits)的特征点数量和影像中特征点总数量之比［7］。

1)旋转变化测试

将影像进行逆时针0°～90°旋转，每隔10°统计特征点数的重复率(表3)。

由表3可得:Harris算子检测旋转变化的重复率最高，即Harris算子的旋转不变性最强;Forstner改进算子检测旋转变化的重复率高于Forstner算子检测旋转变化的重复率，表明Forstner改进算子提高了Forstner算子的旋转不变性;Moravec算子检测旋转变化的重复率最低，表明Moravec算子的旋转不变性最差。Harris算子的旋转不变性最强的原因是:Harris算子使用的是特征点附近区域灰度二阶矩阵，而二阶矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩阵平方根的倒数值，当椭圆旋转时，特征值并不发生变化，并判断特征点的特征值也不发生变化，所以Harris算子的旋转不变性最强［3］。

2)对比度变化测试

利用Matlab 7.1中的对比度增强函数(imajust)进行测试，其中gamma的取值范围为0.5～1.5，每隔0.1统计特征点数的重复率(表4)。

由表4可得:Harris算子检测对比度变化的重复率最高，即 Harris算子的对比度不变性最强; Forstner算子和Forstner改进算子的对比度不变性其次;而Moravec算子的对比度不变性最差。分析Harris算子对比度最强的原因:Harris算子提取特征点时使用了微分算子对影像进行了微分运算，而微分运算对影像密度的拉升或收缩不敏感，即对比度的仿射变换不改变Harris算子兴趣极值的响应位置。

3)抗噪影响测试

利用Matlab7.1中的imnoise函数给影像加入椒盐噪声进行测试，其中噪声的浓度取值范围为0.02～0.2，每隔0.02统计特征点数的重复率(表5)。

由表5可得:几种算子在抗噪方面都不够理想，加入少量噪声后，各算子的重复率都急剧下降，虽然Harris算子检测的重复率最高，但对噪声还是相当敏感，所以建议在点特征提取之前需对数字影像进行去噪处理。比较Forstner改进算子和Forstner算子的重复率可以看出，Forstner改进算子适当提高了Forstner算子的抗噪性。在几种算子中Moravec算子的抗噪性最差，分析其主要原因是该算子检测的窗口函数是二值的，并且为矩形窗口，所以导致其角点响应对噪声敏感。

表3 4种点特征提取算子检测旋转变化的重复率Tab.3 Repetition rates of points detecting the rotation changes with four kinds of interest point detect operators

表4 4种点特征点提取算子检测对比度变化的重复率Tab.4 Repetition rates of points detecting the contrast changes with four kinds of interest point detect operators

表5 4种点特征提取算子检测噪声影响的重复率Tab.5 Repetition rates of points detecting the noise changes with four kinds of interest point detect operators

综上稳定性的测试，分析得出:Harris算子的稳定性较强，Forstner算子的稳定性一般，而Moravec算子的稳定性较差，其中Forstner改进算子适当提高了Forstner算子的稳定性，但效果不明显。

3.4 参数自适性测试

参数自适性主要是判断提取的特征点对设置参数的反应程度，即是参数变化对特征点提取的影响程度。以下是通过真实拍摄影像(图2)进行测试各算子的参数自适性。

1)Moravec算子

Moravec算子提取特征点时需要设置的参数只是兴趣值的阈值，其阈值一般取值为5000～50000，其测试结果见表6。

表6 Moravec算子对参数自适性测试Tab.6 Test results on parameters’suitability of Moravec operator

由表6可得:兴趣值的阈值对提取的特征点数的影响较大，表明Moravec算子的参数自适性较弱。在测试中发现当阈值小于10 000时提取了部分房子和窗户的纹理点，为了减少此种因素得到的伪角点，可以将阈值取大一点，当阈值为20 000时，几乎能提取大部分角点(图2(a))。

2)Harris算子

Harris算子提取特征点时需要设置的参数为兴趣值的阈值和常数k，其测试结果见表7。

由表7可得:兴趣值的阈值对提取的特征点数有一定的影响，但影响不大，而常数k对提取的特征点数的影响较小，表明Harris算子的参数自适性一般。图2(b)为经过大量反复实验测试得出的较好效果图。

3)Forstner算子

Forstner算子提取特征点时需要设置兴趣值的阈值和权值的比例系数f，其测试结果见表8。

表7 Harris算子对参数自适性测试Tab.7 Test results on parameters’suitability of Harris operator

表8 Forstner算子对参数自适性测试Tab.8 Test results on parameters＇suitability of Forstner operator

由表8可得:兴趣值的阈值和常数f对提取的特征点数的影响都很小，表明Forstner算子的参数自适性较强，其中常数f的影响程度大于兴趣值的阈值的影响程度。图2(c)为经过大量反复实验测试得出的较好效果图。

4)Forstner改进算子

Forstner改进算子需要确定两个阈值:一个是初选差分的阈值T，另一个是兴趣值的阈值Tq。其测试结果见表9。

表9 Forstner改进算子对参数自适性测试Tab.9 Test results on parameters’suitability of Forstner improved operator

由表9可得:初选差分的阈值对提取的特征点数的影响较大，而兴趣值的阈值对提取的特征点数的影响较小，表明Forstner改进算子的参数自适性一般。对于有些对比度小的影像，若阈值设置过大，则提取出的点数量过少，在后续的特征匹配中无法得到足够的匹配点对;对于对比度较大的影像，若阈值设置得过小，则提取的特征点数量又会过多，为特征匹配带来严重的运算负担。因此，要实现基于Forstner改进算子的全自动点特征匹配时，应根据图像对比度设置初选阈值，提高其适应性，则能充分发挥其优势。经过反复测试，对于人造测试影像，初选差分的阈值取28～40效果最好，兴趣值阈值取0.45～0.55之间;对于真实拍摄的影像，初选差分阈值范围在20～30之间，兴趣值阈值取0.33～0.45之间，图2(d)为经过反复实验测试得出的较好效果图。

综上测试结果:Moravec算子的算法较为简单，其提取速度较快，而定位精度一般，对影像旋转、对比度变化、噪声影响的反应程度较大使其稳定性较差，同时受阈值的影响较大，其参数自适性较弱; Harris算子虽然在提取速度和参数自适性方面一般，但是其具有较强的稳定性，对影像旋转、对比度变化、噪声影响的反应程度较小;Forstner算子的明显优势就是其定位精度较高和参数自适性较强，然而其算法较为复杂导致运算速度较慢，并且对影像的对比度变化和噪声影响的反应程度较大使其稳定性一般;Forstner改进算子的最大改进就是提高了Forstner算子的运算速度，其运算速度在几种算子中最快，同时也适当的提高了Forstner算子的旋转不变性和抗噪强度。

4 改进算子

根据综合测试得:Harris算子具有较强的稳定性，但定位精度一般，其定位精度只能达到像素级，然而Forstner算子的定位精度较高，所以可以将两种算子结合进行特征点提取。由于Harris算子的参数自适性一般，其中兴趣值的阈值对提取的特征点数有一定的影响，然而兴趣值的阈值是通过经验值手动调整得到的，其提取效率较低，劳动强度较大，为了提高Harris算子的参数自适性，本文通过区域特征点兴趣值的均值作为兴趣值阈值的方法，实现了自动检测兴趣值的阈值，提高特征点的提取效率。以下是改进算子的计算步骤:

1)提取区域特征点。以7×7的像素窗口将整幅影像进行分割，得到每个小区域，然后在每个小区域里通过Harris算子检测该区域兴趣值R最大的像素点，作为该区域的特征点;

2)提取整幅影像的特征点。求取区域特征点兴趣值的平均值作为Harris算子的阈值，将大于该阈值的区域特征点作为整幅影像的特征点;

3)特征点的亚像素定位。采用Forstner算子加权中心化的方法［8］，以局部最大特征值的Harris算子提取特征点作为中心，在一定大小的窗口(如3× 3窗口)范围内，将原像素坐标改为以最大权点为原点的独立坐标，然后利用该窗口内所有点的特征值R拟合二次曲面，求解二次曲面中特征值R的最大点位，并作为特征点亚像素精度的坐标点位，由此将特征点的精度提高到亚像素级。

利用如图3所示的影像测试改进算子的定位精度，其测试结果如表10所示，根据测试结果可得改进算子提高了Harris算子的定位精度，具有较高的定位精度。利用如图2所示的影像测试改进算子的参数自适性，其测试结果如表11所示。根据测试结果得出:通过检测区域特征点兴趣值的平均值作为阈值的方法，具有较强的参数自适性，并且避免了特征点聚簇的现象和手动设置阈值的不确定性。虽然改进算子的提取速度一般，但是其具有Harris算子较强的稳定性，并且具有较高的定位精度和较强参数自适性，所以该算子在数字近景摄影测量中具有较强的可行性。几种点特征提取算子的比较结果见表12。

表10 Harris算子与改进算子的精度比较Tab.10 Comparison between accuracies of Harris operators and improved operator

表11 改进算子的参数自适性测试Tab.11 Test results on parameters’suitability of improved operator

表12 几种点特征提取算子的比较Tab.12 Comparison among several kinds of interest point detect operators

5 结论

分别利用一幅包括多种类型角点的人造测试影像和一幅真实拍摄的影像测评各算子的提取速度、定位准确性、稳定性、参数自适性，比较得出各算子的优缺点，并在此基础上提出了一种改进算子，经过实验测试结果表明:改进算子具有较强的稳定性和较高的定位精度，同时具有自动设置阈值的特点，避免了手动设置阈值的不确定性，提高了特征点的提取效率，所以其在数字近景摄影测量中具有较强的可行性。

1 张祖勋，张剑清.数字摄影测量学［M］.武汉:武汉大学出版社，2002.(Zhang Zuxun and Zhang Jianqing.Digital photogrammetry［M］.Wuhan:Wuhan University Press，2002)

2 余晨，金飞，石娟.基于灰度信号的点特征提取方法比较研究［J］.测绘信息与工程，2009，34(6):44-45.(Yu Chen，Jin Fei and Shi Juan.Several intensity based methods for image feature point extraction［J］.Journal of Geomatics Dec，2009，34(6):44-45.)

3 王永明，王贵锦.图像局部不变性特征与描述［M］.北京:国防工业出版社，2010.(Wang Yongming and Wang Guijin.Image local invariant features and descriptors［M］.Beijing:National Defense Industry Press，2010)

4 张春美，龚志辉，黄艳.几种特征点提取算法的性能评估及改进［J］.测绘科学技术学报，2008，25(3):231-234.(Zhang Chunmei，Gong Zhihui and Huang Yan.Performance evaluation and improvement of several feature point detectors［J］.Journal of Geomatics Science and Technology，2008，25 (3):231-234)

5 Rodehorst V and Koschan A.Comparison and evaluation of featrue point detectors［A］.Proc.5th International Symposium Turkish-German Joint Geodetic Days“Geodesy and Geoinformation in the Service of our Daily Life”［C］.Technical University of Berlin，2006:8-15.

6 张春美.特征点提取及其在图像匹配中的应用研究［D］.解放军信息工程大学，2008.(Zhang Chunmei.Study on feature point detecting and its application image matching［D］.PLA Information Engineering University，2008)

7 Schmid C，Mohr R and Bauck hage C.Evaluation of interest point detectors［J］.International Journal of Computer Vision，2000，37(2):151-172.

8 耿则勋，张保明，范大昭.数字摄影测量学［M］.北京:测绘出版社，2010.(Geng Zexun，Zhang Baoming and Fan Dazhao.Digital photogrammetry［M］.Beijing:Surveying and Mapping Press，2010)

COMPARATIVE STUDY ON INTEREST POINT DETECT OPERATORS BASED ON IMAGE’S GRAY AND IMPROVEMENT

Wang Qichun1，2，3)，Guo Guangli1，2，3)，Zha Jianfeng1，2，3)and Liu Shen3)

(1)China University of Mining and Technology，Key Laboratory for Land Environment and Disaster Monitoring of SBSM，Xuzhou 221116 2)China University of Mining and Technology，Jiangsu Key Laboratory of Resources and Environmental Information Engineering，Xuzhou 221116 3)China University of Mining and Technology，Shool of Environment Science and Spatal Informatics，Xuzhou 221116)

This method based on image’s gray to detect the interest pointis mainly includes Moravec operator，Harris operator，Forstner operator and the improved Forstner operator nowadays，and there are some differences in the detect speed，positioning accuracy，stability between different operators.In this paper the detect speed，positioning accuracy，stability and parameters’suitability of each operator are evaluated by testing a artificial test image and a really taken image，and the test results show the advantages and disadvantages of each operator.A improved operator is proposed based on the test results.The study results show that the improved operator has the characteristics of strong stability，high positioning accuracy and auto-setted threshold.

interest point detect;Moravec operator;Harris operator;Forstner operator;improved operator

1671-5942(2012)02-0148-07

2011-10-28

国家自然科学基金重点项目(50834004);国家自然科学基金青年基金(41104011)

王启春，男，1987年生，硕士研究生，主要研究方向为数字摄影测量与变形监测.E-mail:wqcls@cumt.edu.cn

P207

A