GNSS/Pseudolites导航定位中的伪卫星优化模型研究*

姜昆王坚刘超

(中国矿业大学国土环境与灾害监测国家测绘局重点实验室，徐州 221116)

GNSS/Pseudolites导航定位中的伪卫星优化模型研究*

姜昆王坚刘超

(中国矿业大学国土环境与灾害监测国家测绘局重点实验室，徐州 221116)

针对GNSS/Pseudolites组合系统的伪卫星优化布设问题，指出了多指标评价体系下的GNSS系统中伪卫星加入的必要性，构建了基于方位角、高度角及观测历元的多指标评价体系四维模型，并通过实测数据进行实验分析，结果表明:伪卫星的加入所带来的可见卫星个数及低高度角处信息的变化可有效地增强系统的可靠性，提高了系统的定位精度;全景显示下的PDOP值与内可靠性值的最优区域变化相似但分布不同;PDOP、内可靠性、耗资等多因素约束的综合定权可有效协调各个指标，为选择最优系统提供可靠依据并在全景显示下有效地解决伪卫星优化GNSS系统的高效选址问题。

内部可靠性;绝对定位精度因子;GNSS/PLs组合定位;网形优化;综合评价体系

1 引言

伪卫星因其高度角极低且信号不经过电离层的显著特点可弥补GNSS星座卫星分布不良［1，2］、信号不佳、受高度截止角制约等问题。对于伪卫星加入的位置及个数目前主要是通过设计数个仿真实验或基于一定经验进行较大样本的方案比较确定［3，4］。在一些情况下，实际现场仅需满足一定要求的系统可靠性［5］、可用性及定位精度，过多伪卫星的加入必定带来过多的耗资，因而采用PDOP值、内部可靠性、耗资综合评定GNSS/伪卫星增强系统成为一种可行方案。鉴于此，本文尝试基于综合评价体系分别建立以时间历元、高度角、方位角为自变量，精度因子、内部可靠性为因变量的四维模型，分别对观测时段内任意时刻所有可能布设方位所对应的精度、可靠性值进行全景显示，进而参考实际环境综合评价最优伪卫星布设方案。

2 理论基础

2.1 可靠性指标

以一定的统计检验方法所能发现的观测值粗差的大小称为内部可靠性。依导航卫星分布的几何结构，并由误差方程系数矩阵A，观测值权阵P求得改正数的协因数阵为［6］:

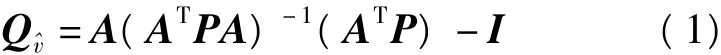
对于给定的置信水平及相关观测值其可发现粗差的下界值可表示为:

其中ei是单位向量，设第i个元素为1则表明对第i个值进行检验;δ0是采用w进行粗差检验的非中心化参数，并由下式给出:

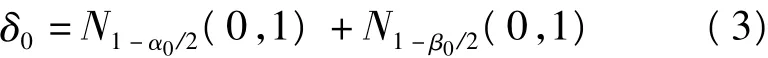
其中α0为显著性水平，β0为检验功效。此处取α0=0.01，β0=0.2。

此外，对于内可靠度si常有ci≤si≤di(ci、di均为正常数)，若max{inf(si)}＜min(ci)则视为不可靠。

未被发现的模型误差对平差结果的影响称为导航定位的外部可靠性，外部可靠性可看做某观测值下界值粗差对参数评估带来的偏差，评价公式为:

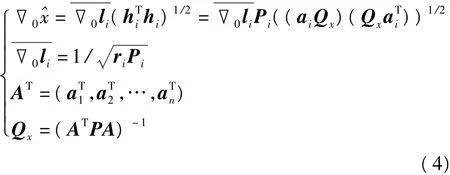
其中l为观测值权向量。

2.2 绝对定位精度因子(PDOP)

不同历元下，不同卫星同步观测的伪距观测方程中含有观测站坐标及接收机钟差四个参数［7］，设(X，Y，Z)T、(δx，δy，δz)分别为观测站坐标的近似值与改正数，将伪距观测方程进行泰勒展开并令:

若可见卫星数n≥4，则依据卫星位置及初始测站坐标并令cδtk=δρ，得伪距观测线性化方程组形式为:

依最小二乘知

由式(8)可知，Qx在t时刻未知参数的协因数阵在空间直角坐标中的一般形式为:

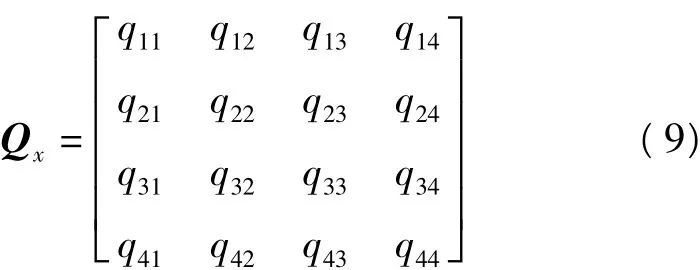
实际生产中常需要提高某方向上的定位精度，故常采用其在大地坐标系中的表达形式来估算测站点的位置精度，依据方差与协方差传播定律可得:

t时刻的绝对定位精度因子为:

2.3 系统可用性综合评价体系

系统单约束评价多局限于精度方面的控制，缺乏对系统可靠性、可用性及组建最优系统的资费等方面的考虑。单约束条件下的系统不够稳固，过多追求精度或可靠性也将使得系统的其他方面指标过弱。此外，多质量控制指标之间常常相互矛盾，指标的各自最优区域难以相互协调。因此最优方案需要通过使用综合评估的功能函数［8］来获得，从而进一步反映各要素之间的权关系。

多个约束条件的最优设计［9］的表达式为:

其中:λ1、λ2、λ3是依据实际需要为3个约束条件精度、可靠性、资费指标选择的权重。

对于式(12)需考虑3种特殊情形:

1)cost=min(precision)≥reliabilityamp;const≥const;

2)precision=max(reliability)≥cos tamp;const≥const;

3)reliability=max(precision)≥cos tamp;const≥const。

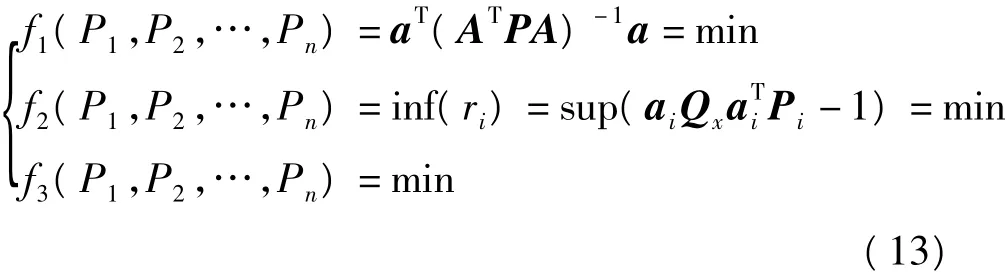
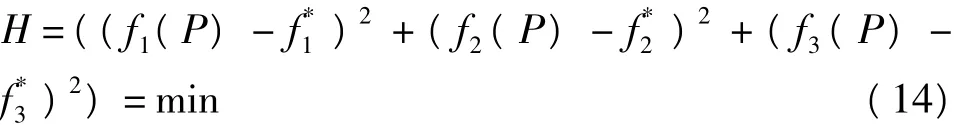
3 伪卫星优化设计技术路线

对于给定测站位置，其PDOP及内可靠性值仅受卫星(包括伪卫星)与测站相对位置即组合系统图形结构的影响，即可看作受卫星的方位角a、高度角e以及时间t的影响，故建立以(a，e，t)为自变量，PDOP或内可靠性为因变量的四维模型，考虑到资费因素主要与伪卫星布设的个数相关，因此主要对PDOP与内可靠性(以下均以Internal表示)进行加权评价:

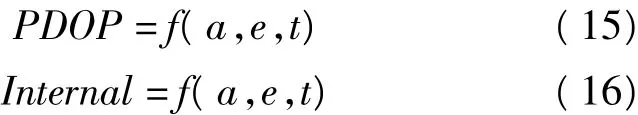
其中f(·)和f'(·)为映射函数，a∈［0°，360°)，e∈［-90°，90°］，t≥0;该四维模型可对PDOP与Internal值的变化进行全景显示，为选择伪卫星的加入位置提供可靠的依据。

依四维模型直接进行伪卫星优化布设较为复杂，因而给出布设流程(图1):选定一定的时间间隔，沿时间轴截取PDOP及内可靠性值的剖面，依据PDOP值选取较优区域作为备选，然后综合备选区域与内可靠性剖面进行最优判断，若不为最优则重新选择备选区域，若为最优则考虑实际现场环境，选定可布设的最优位置，并检验PDOP及内可靠性沿时间轴的变化曲线，检验PDOP及内可靠性值在观测时段内是否是平滑可靠，进而进行最终的方案确定。第一颗伪卫星选定之后，将其看作是GNSS星，再加入第二颗伪卫星，重复上述步骤，从而确定伪卫星加入的个数与及最终的布设方案。

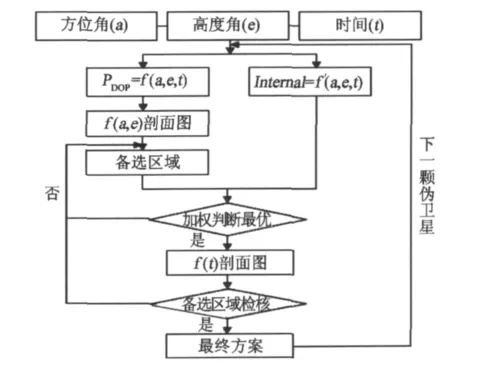
图1 伪卫星最优布设流程图Fig.1 Flow chart of optimal pseudolites locations

4 实验分析

为验证理论及模型的可行、可用性，实验采用布设于中国矿业大学环境与测绘学院的强制对中设备采集的实测数据进行相关实验分析与评价。数据采集采用1台天宝R8接收机于2011-04-10日进行数据采集，观测时段内，设站点(North)处的卫星分布如图2所示。数据采样频率为1 Hz，采样数据长度60分钟。以PDOP值及内部可靠性指标为例，说明多指标评价系统可用性的过程，进行相关的分析与评价。

实验分别对GNSS星座图形结构较弱的6颗可视卫星情形及GNSS星座图形结构较好的9颗可视卫星情形进行分析，分析伪卫星的加入对定位精度及系统内部可靠性的影响，同时分析伪卫星的最优选址。

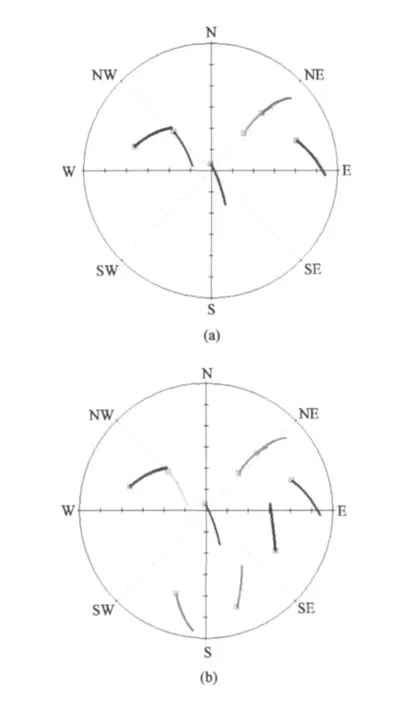
图2 可视卫星分布Fig.2 Distribution of visible satellites

设站点North处可视卫星天空图如图2(a)，受环境制约，设站点南方受建筑物遮挡，可见卫星仅为6颗，取2 000个历元进行分析，其PDOP值为3.3～3.6，Internal值为8.03～8.17。以设站点(North)为中心，高度角为［-90°，90°］，方位角为［0°，360°)进行伪卫星的全景布设，800历元处剖面如图3、4所示。分析可知，加入一颗伪卫星后，PDOP值为1.94～3.29，Internal值为6.285～8.04。在方位角为［170°，250°］范围内PDOP值最大可减少至1.94～2.109，在高度角［-60°，50°］范围内可靠性最大可减少至6.285～6.487，而在方位角［0°，50°］范围内的布设较差，需要依据实际情况特别关注。

但是，精度与可靠性的局部最优区域难以协调，单指标(精度或可靠性)的评价体系难以获得更为优化的星座网形，800历元处精度、可靠性综合评价指标(精度影响系数为0.6，可靠性影响系数为0.4)随高度角、方位角变化的剖面图如图5所示。如表1所示，该综合评价指标下，星座PDOP值为2.233，Internal值为6.634。

图3 不同位置布设一颗伪卫星时对应的PDOP值Fig.3 PDOP values corresponding to one PLs laid at different positions

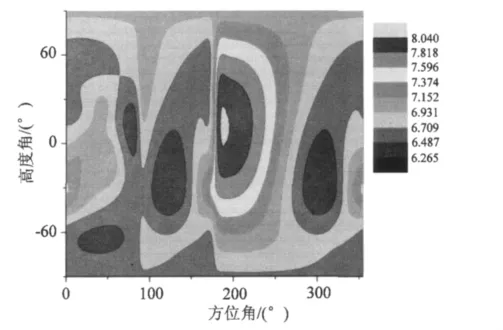
图4 不同位置布设一颗伪卫星时对应内的可靠性值Fig.4 Internal reliability values corresponding to one PLs laid at different positions

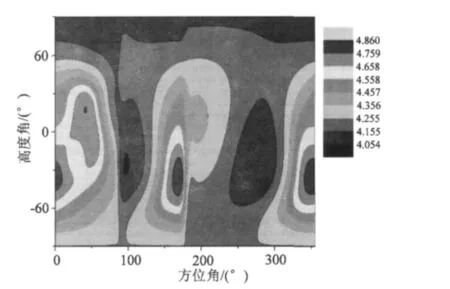
图5 6颗可视卫星下综合评价Fig.5 Comprehensive evaluation with 6 visible satellites

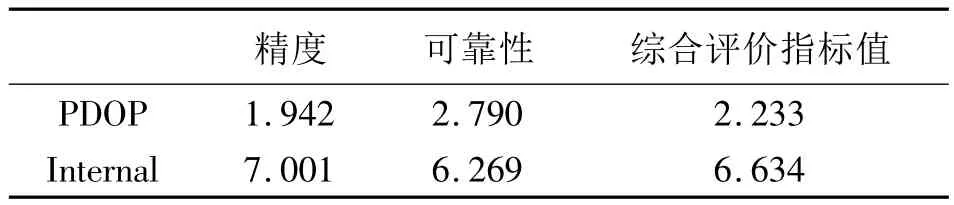
表1 6颗可视卫星下精度、可靠性及综合评价指标值Tab.1 PDOP，internal reliability values and evaluation values with 6 visible satellites

对于星座可视卫星较多，图形结构较好的情形，实验设站点仍选择North点，取消遮挡。实验时段内，连续跟踪卫星数为9颗，可视卫星天空图如图2 (b)所示。其在实验时段内的PDOP值达到2.070～2.261，Internal值达到5.415～5.430。仍以基准站North为中心，高度角为［-90°，90°］，方位角为［0°，360°)进行伪卫星的全景布设，建立对应的PDOP及Internal四维模型，如图7、8所示。分析知在GPS星座拥有9颗可视卫星情形下，一颗伪卫星在部分区域内的引入依然可将 PDOP值优化至1.010～1.198，Internal值优化至5.158～5.225。表2给出单指标及综合评价指标下的PDOP及Internal值。可见，精度最高时其可靠性甚至低于加入伪卫星前的星座。

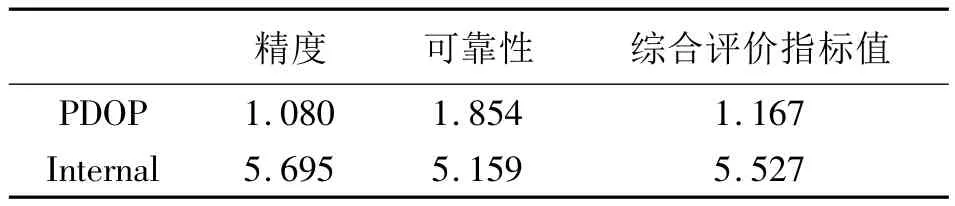
表2 9颗可视卫星下精度、可靠性及综合评价指标值Tab.2 PDOP，internal reliability values and evaluation values with 9 visible satellites

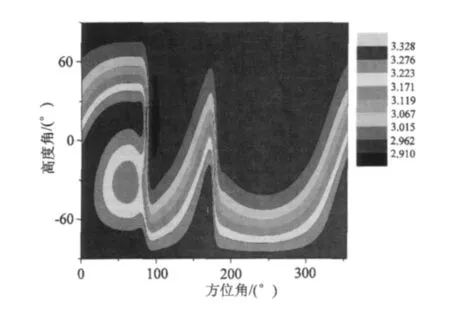
图6 9颗可视卫星下的综合评价结果Fig.6 Comprehensive evaluation with 9 visible satellites

图7 不同位置布设一颗伪卫星时对应的PDOP值Fig.7 PDOP values corresponding to one PLs laid at different positions

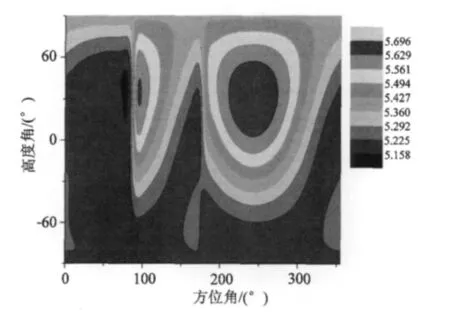
图8 不同位置布设一颗伪卫星时对应的内可靠性值Fig.8 Internal reliability values corresponding to one PLs laid at different positions

对于可视卫星数较少情形，单颗伪卫星的加入可有效优化星座的定位精度及可靠性，伪卫星的加入除影响设站点可视卫星数之外，其提供的高度角［-90°，90°］处信息尤其是低高度处的信息可有效地提高系统精度及系统的可靠性。对可视卫星数较多的情形，伪卫星的加入可使系统满足实际应用中对精度或可靠性的特殊要求。第一颗伪卫星选定之后将其视为GNSS星座一部分，重复上述过程进行下一颗伪卫星位置的选定，而可加入伪卫星的个数则受耗资及实际需求指标的综合制约。

5 结论

针对GNSS/伪卫星组合定位系统，利用实测数据以伪距单点定位模式组建方差阵，构建以方位角、高度角、时间历元为自变量，内部可靠性值与PDOP值为因变量的四维模型进行伪卫星加入所有可能位置后的PDOP值与内部可靠性值变化的全景显示，并用PDOP值及内部可靠性值进行综合评价以确定伪卫星加入的个数与位置，实验证明该方法直观、有效。此外，依实验结果无论当前GNSS星座图形结构的优劣，伪卫星的加入因其提供的低高度角处信息，整个系统的定位精度及可靠性会得到有效提升，但仍需控制伪卫星加入的个数，以满足实际应用的需求。

1 Liu Chao，Zhou Feng and Liu Yan.GPS/Pseudolites technology based on EMD-Wavelet in the complex field conditions of mine［R］.The 6th International Conference on Mining Scienceamp;Technology，2009，10.

2 刘超，等.GPS伪卫星技术在露天矿边坡监测中的应用研究［J］.煤炭学报，2010，(5):755-759.(Liu Chao，et al.GPS/Pseudolites technology for the slope deformation monitoring in open-pit mine［J］.Journal of China Coal Society，2010，(5):755-759)

3 何秀凤，等.GPS伪卫星组合定位方法及在变形监测中的应用［J］.南京航天航空大学学报，2007，39(6):795-799.(He Xiufeng，et al.Integration of GPS and pseudolites for deformation monitoring［J］.Journal of Nanjing University of Aeronauticsamp;Astronautics，2007，39(6):795-799)

4 王晖辉，等.地面伪卫星测试环境中关于选址系统的建模仿真［J］.系统仿真学报，2009，21(2):371-373.(Wang Huihui，et al.Modeling and simulation of site selection system in gound pseudolites test system［J］.Journal of System Simulation，2009，21(2):371-373)

5 李德仁，袁修孝.误差处理及可靠性理论［M］.武汉:武汉大学出版社，2002.(Li Deren and Yuan Xiuxiao.Error processing and reliability theory［M］.Wuhan:Wuhan University Press，2002)

6 Cross P A，Hawksbee D J and Nicolai R.Quality measures for differential GPS positioning［J］.The Hydorgraphic Journal，1994，72:17-22.

7 李征航，等.GPS测量与数据处理［M］.武汉:武汉大学出版社，2010.(Li Zhenghang，et al.GPS surveying and data processing［M］.Wuhan:Wuhan University Press，2010

8 Muller，H.A numerically efficient solution of the second order design problem［J］.Bulletin Geodesique，1984，(1): 85-99.

9 Xu Peiliang.Multi-objective optimal second order design of networks［J］.Bulletin Géodésique，1989，63(3):297-308.

STUDY OF PSEUDOLITES OPTIMIZATION MODEL IN GNSS/PSEUDOLITES NAVIGATION AND POSITIONING

Jiang Kun，Wang Jian and Liu Chao
(China University of Mining and Technology，Key Laboratory for Land Environment and Disaster Monitoring of SBSM，Xuzhou 221116)

Aiming at optimal construction of pseudolites in GNSS/Pseudolites(PLs)combined system，this paper pointed out the necessity of PLs’joining in GNSS，and built a four-dimensional(4-D)model based on azimuth angel，elevation angel and observed epochs.Then，an experiment was taken to test the model，and the results show that the increasing number of visible satellites and the changing information of low-elevation satellites can enhance the reliability of the system and improve positioning accuracy.Panorama shows that variations of the PDOP value and the reliability value within the optimal region are similar but the distributions are different.The weight constrained by the PDOP，internal reliability，cost and other factors can be effective coordinate indexes for selecting optimal system and provide reliable basis for effectively solving the problem of locating PLs for GNSS/PLs optimization.

internal reliability;PDOP(position dilution of precision);GNSS/PLs combination system;network optimization;comprehensive evaluation system

1671-5942(2012)02-0134-06

2011-10-20

国家自然科学基金青年基金(40904004);教育部博士点基金(新教师)(200802901516);教育部博士点基金(200802900501);江苏省自然科学基金(BK2009099);江苏省普通高校研究生科研创新计划项目(CXLX11_0321);江苏省“青蓝工程”资助项目;江苏高校优势学科建设工程资助项目

姜昆，男，1989年生，硕士研究生，从事GNSS、PLs组合导航方面的研究.E-mail:jk408466382@163.com

P207

A