协方差函数的选择对GPS高程拟合精度的影响*

李成仁 岳东杰 金保平

(河海大学测绘科学与工程系，南京 210098)

协方差函数的选择对GPS高程拟合精度的影响*

李成仁 岳东杰 金保平

(河海大学测绘科学与工程系，南京 210098)

阐述最小二乘配置的原理，给出先验方差协方差估计方法，通过实例分析了采用最小二乘配置法的有效性，比较了不同协方差函数对拟合精度的影响及拟合点的分布对协方差函数、拟合结果的影响。

模型误差;最小二乘配置;协方差函数;GPS高程拟合;拟合精度

1 引言

在工程测量领域，最常用的高程异常拟合方法是数学曲面拟合法，然而常规方法只是拟合出与高程异常相近似的趋势面来代替拟合区域的似大地水准面，并没有顾及到似大地水准面的物理性质。实际上，由于地壳的不均衡和地形起伏的影响，似大地水准面是一个非常复杂且不规则的曲面，任何拟合方法总与之有一定的差异。这种差异可以解释为由于拟合模型的不准确造成，因此不同点的高程异常拟合误差实际上包含两部分:测量误差和选取的模型与实际似大地水准面的差异。显然，常规的最小二乘拟合将两部分综合作为测量误差来处理是不严密的，拟合结果必然受到影响。因此在数据处理过程中必须顾及这种差异的影响，这正是最小二乘配置法(LSC)［1］的思想，该法将这种选取的模型与实际似大地水准面的差异看作是随机函数，即所谓的信号来对待，在估计非随机的趋势部分的同时，也估计这种模型差异的随机部分，从理论上讲可以取得较好的效果。然而在实际采用最小二乘配置法时，其成功的关键是合理确定信号的方差协方差阵。协方差函数的严密表达式难以准确获取，实际中通常根据观测或实验(即估计)得到的经验协方差函数来近似表达，因此协方差函数的确定与选择直接影响着估计值的精度。基于此，本文重点研究协方差函数的选择对GPS高程拟合结果的影响。

2 最小二乘配置的基本原理

最小二乘配置的函数模型一般表示为

其随机模型是:X和X'的先验期望:E(X)= μX，E(X')=μX';X和X'的先验方差和协方差:var (X)=DX，var(X')=DX'，cov(X，X')=DXX';Δ的数学期望和方差:E(Δ)=0，var(Δ)=DΔ;Δ关于X和X'的协方差:cov(Δ，X)=DΔX，cov(Δ，X')=DΔX'，实际应用中噪声Δ与X，X'是相互独立的，即DΔX=0，DΔX'=0。

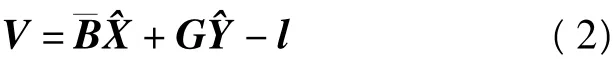
从而推得:

单位权中误差

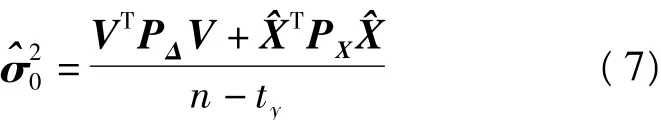
式中，ty为倾向参数Y的个数。

3 先验方差协方差的估计

信号的方差协方差阵的基本思想为:预先选择一个符合协方差函数条件的、形式比较简单的函数作为协方差函数，根据观测值采用拟合的方法求得所选协方差函数中的待定参数，然后通过拟合得到的协方差函数确定信号的方差协方差阵。

关于协方差函数，国内外专家学者进行了一系列研究［2-5］。目前常用的协方差函数有［6］:

1)高斯(Gauss)函数

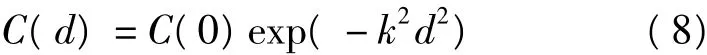
2)希尔伏宁(Hirvonen)函数

3)似高斯(Gauss)函数

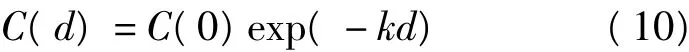
上面各式中C(0)表示距离为零时信号间的协方差，其实质就是信号的方差，即为协方差矩阵中的对角线元素，k为待定参数，d为两点间的距离。其中C的先验值的计算采用

式中:nd为相距为d的对点数;i、j为对点的点号，C是任意两个相距为d的数据点之间的先验协方差;［］表示求和;si为异常位的信号值。一般来讲，严格等于所选距离d的对点几乎没有。这里可以把d选为整千米数，即d=1，2，3，…，把距离d满足其0.5千米范围内的所有对点均认为满足点距为d的对点，这样，所有的数据点都参与了初始协方差的计算，并且没有任何一对点被重复计算。在实际确定协方差函数时，数据点之间的距离d的大小应进行适当的选定，当数据变化较平缓时，距离d可以大一些，如果数据变化较快，应当缩小间距。

由于高斯函数和希尔伏宁函数以距离的平方为变量，其函数值随距离的增大而迅速减小;根据相关系数公式［7］

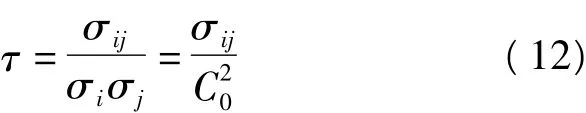
可见这两个函数所表现出的数据点之间的相关性随距离的增大而迅速减弱，而似高斯函数以距离为变量，函数值的变化相对就比较缓和。因此当经验协方差函数与实际的逼近场比较符合时，它就能较好地反映各数据点之间的相关性。

4 算例分析

为了分析协方差函数的选择对最小二乘配置的影响，选取某地航测GPS控制网测量数据进行GPS高程拟合计算［8］。共收集该测区内112个GPS、水准重合点，GPS采用E级施测，水准采用四等水准测量施测。根据GPS大地高、四等水准计算出的高程异常绘制该区域的高程异常等值线图如图1所示。从图1可以看出，该区域高程异常分布比较平缓，故采用平面拟合模型。

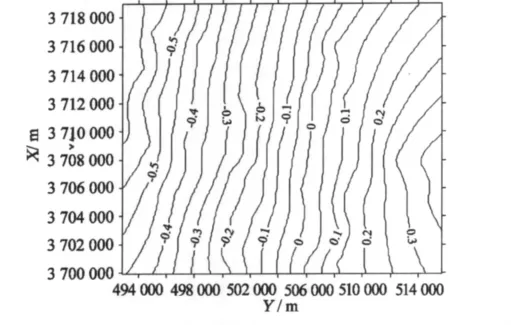
图1 高程异常等值线Fig.1 Isolines of height anomaly

4.1 不同协方差函数对拟合结果的影响

为了能够检核拟合的效果，选取均匀分布的87个点作为拟合点，其余25个点作为检核点进行整体拟合。

首先采用普通最小二乘(LS)进行高程拟合，对得到的残差按0.01 m间隔统计各间隔出现的点数，对应的直方图见图2。

图2 拟合点残差分布Fig.2 Distribution of fitting points errors

由图2可以发现，普通最小二乘的拟合残差不符合正态分布，说明拟合残差中不仅包含各种偶然误差，还包含由于拟合模型不准确造成的模型误差。

使用普通最小二乘拟合剔除趋势项后，再根据式(11)计算不同间隔d的协方差C(d)。选取式(8)、(9)、(10)3种不同的经验协方差函数拟合，求得的待定系数见表1。

根据拟合得到的协方差函数，计算拟合点信号协方差阵 DX，拟合点与检核点的方差协方差阵DX'X。利用最小二乘配置理论重新计算倾向参数和信号的估值S和S'。根据拟合方程计算拟合点的高程异常，并与理论的高程异常比较，得到的拟合点和检核点的拟合残差见图3和图4。

表1 各经验协方差函数的待定系数Tab.1 Undetermined coefficients of experient covariance function

其中信号方差C(0)=28.364×10-5m2。

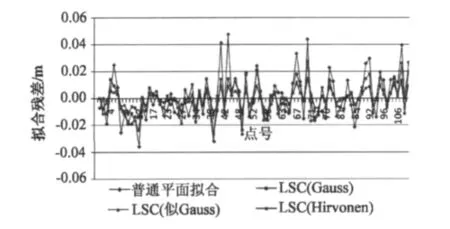
图3 拟合点拟合残差Fig.3 Fitting errors of fitting points

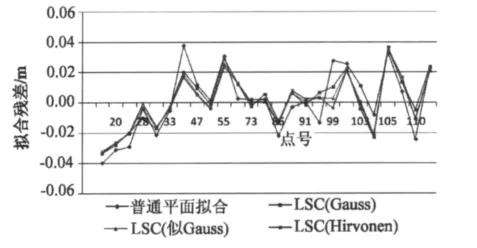
图4 检核点拟合残差Fig.4 Fitting errors of check points

同样地，对得到的残差按0.01 m间隔统计各间隔出现的点数，对应的直方图见图2。

内符合精度根据式(7)计算，外符合精度根据检核点的拟合残差按

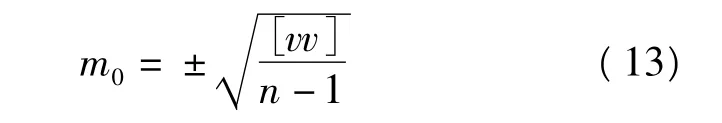
计算。式中v为拟合残差，n为检核点的个数。表2列出了几种不同平差方法的内、外符合精度。

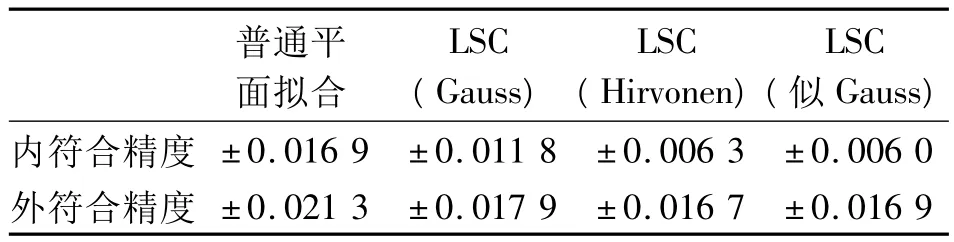
表2 内、外符合精度比较表(单位：m)Tab.2 Comparison of inner and outer accuracies(unit：m)

从计算结果可以看出:

1)即使该测区地势较为平坦，但运用普通的平面拟合模型仍会含有较大模型误差。由图2可以看出，运用最小二乘配置法处理后，模型误差得到有效控制，拟合精度大幅提高。

2)以高斯(Gauss)函数作为协方差函数，内符合精度较低，这主要是因为高斯函数以距离的平方为变量，反映在图像上，曲线变化较陡，不符合该地区高程异常的变形特点。

3)以希尔伏宁(Hirvonen)函数作为协方差函数时，虽然外部符合精度较高，但对个别点，推估值与己知值之差有时会出现较大的波动，不太稳定;但以似高斯函数作为协方差函数，其外部符合精度较高，较差也十分稳定。

4)一般地，以似高斯函数作为协方差函数，不管是内符合精度还是外符合精度，都可以得到较满意的结果。

4.2 拟合点的分布对协方差函数及拟合结果的影响

为了分析拟合点的分布对协方差函数拟合的影响，作者根据点的分布分几种情况选取其中50个非均匀分布的点作为拟合点，以似高斯函数为协方差函数进行拟合试算，并与采用87个均匀分布点的结果进行比较，结果相似。表3列出了其中一种情况的拟合结果。

表3 协方差函数的待定系数及高程拟合精度(单位：m)Tab.3 Undetermined coefficients of covariance function and the fitting accuracy(unit：m)

可见，拟合点的分布对协方差函数的拟合有一定的影响，从而也影响最小二乘配置的拟合精度。从本算例来看，尽管协方差函数有所差别，但对最终结果的影响并不是很大，这说明协方差函数的拟合对拟合点分布的均匀性要求不是那么敏感，因此在实际选取协方差函数拟合点时，可以稍放宽要求。

5 结论

由于常规最小二乘拟合法不严密地将模型误差归入观测误差进行处理，致使拟合后的残差仍含有较大模型误差。通过采用最小二乘配置法，将模型误差作为具有先验性质的信号处理，可以有效控制模型误差对结果的影响［9］。协方差函数的确定直接影响最小二乘配置的结果。针对GPS高程拟合问题，通过比较分析不同协方差函数的计算结果得出:不同协方差函数对最小二乘配置法解算结果影响较大，在实际应用时，应结合实际情况选择合适的协方差函数。在地势较为平坦地区，以似高斯函数作为协方差函数时，不管是内符合精度还是外符合精度，都可以得到较满意的结果。

1 沙月进.最小二乘配置法在GPS高程拟合中的应用［J］.测绘信息与工程，2000，(3):3-5.(Sha Yuejin.Application of the least square collocation in GPS height fitting［J］.Journal of Geomatics，2000，(3):3-5)

2 Moritz H.Least-squares collocation［J］.Reviews of Geophysies and Space Physics，1975，16:421-430.

3 Tseherning.Covariance expressions for second and lower order derivatives of the anomalous potential［R］.Dep of Geod Sci.，Ohio state University Columbus，1976.

4 周江文，王跃进.抗差拟合推估［A］.抗差估计论文集［C］.北京:测绘出版社，1992，69-75.(Zhou Jiangwen and Wang Yuejin.Robust fitting estimation［A］.Proceedings of Robust Estimation［C］.Beijing:Surveying and Mapping Press，1992，69-75)

5 杨元喜，等.四维整体大地测量的解算及其协方差函数的确定［J］.军测科技，1990，(4):3-7.(Yang Yuanxi，et al.Procedure of four dimensional integrated geodesy and determination method of covariance function［J］.Technology of Military Surveying and Mapping，1990，(4):3-7)

6 张勤，张菊清，岳东杰.近代测量数据处理与应用［M］.北京:测绘出版社，2011.(Zhang Qin，Zhang Juqing and Yue Dongjie.Modern measured data processing and application［M］.Beijing:Surveying and Mapping Press，2011)

7 刘念.拟合推估的质量理论［D］.解放军信息工程大学，2003.(Liu Nian.Quality theory of collocation［D］.The PLA Information Engineering University，2003)

8 李文林.GPS技术在航空摄影地面控制测量中应用研究［D］.河海大学，2008.(Li Wenlin.Application of GPS techniques in ground control survey of aerial photogrammetry［D］.Hohai University，2008)

9 姚道荣，等.最小二乘配置与普通Kriging法的比较［J］.大地测量与地球动力学，2008，(3):77-82.(Yao Daorong，et al.Comparison between least squares collocation and ordinary Kriging［J］.Journal of Geodesy and Geodynamics，2008，(3):77-82)

STUDY ON EFFECT OF CHOICE OF COVARIANCE FUNCTION ON GPS HEIGHT FITTING ACCURACY

Li Chengren，Yue Dongjie and Jin Baoping
(Department of Surveying and Mapping Science and Engineering，Hohai University，Nanjing 210098)

The key of least square collocation method is to determine the covariance function of experience reasonably.On the basis of necessity of least square collocation in GPS height fitting，the principle of least square collocation is expounded，a priori variance-covariance estimation method is given，the effectiveness of least square collocation is analyzed by an example，the different covariance functions affecting fitting accuracy and the distribution of fitting points affecting covariance function and fitting accuracy are compared.Finally，the applicable conditions of some commonly used covariance function is summarized，and some instructional views in applications are given.

model errors;least square collocation;covariance function;GPS height fitting;fitting accuracy

1671-5942(2012)02-0082-04

2011-10-11

国家自然科学基金(51079053)

李成仁，男，1989年生，硕士研究生，研究方向:大地测量与测量工程专业，测绘数据处理.E-mail:lichengren1989@126.com

P207

A