基于超级计算机平台的并行解技术在卫星重力测量中的应用*

聂琳娟 申文斌 王正涛 金涛勇

(1)武汉大学测绘学院，武汉 430079 2)湖北水利水电职业技术学院，武汉430070)

基于超级计算机平台的并行解技术在卫星重力测量中的应用*

聂琳娟1，2)申文斌1)王正涛1)金涛勇1)

(1)武汉大学测绘学院，武汉 430079 2)湖北水利水电职业技术学院，武汉430070)

分析超级计算机平台的并行解技术应用于卫星重力测量中的相关问题，对涉及的矩阵运算并行化给出了数值计算和分析，并利用卫星重力扰动位观测基于最小二乘直接解法，比较了OpenMP和MPI两种并行化技术的计算效率。

卫星重力;并行计算;重力位模型;OpenMP;MPI

1 前言

随着卫星重力探测计划的成功实施，地球重力场的研究成为国际大地测量学的热点问题。如何高效深入地利用当前(CHAMP、GRACE)和未来(GOCE)卫星任务获取的数据成为真正具有挑战性的任务。随着卫星观测数目的不断增多，数据处理将成为地球重力场恢复中的一个关键问题。对于GRACE卫星的数据，如果30秒的数据采样，一个月将有86 400个观测值，如果计算一年平均重力场模型，观测值将达到1 036 800个，众所周知，对于观测方程的系数阵的形成，勒让德函数的计算是最耗时间的过程，在GS80服务器上，如果球谐展开到90阶，一个观测将花费1.5秒计算时间，如果展开到120阶，将花费4秒，因此，对于GRACE卫星任务，预期恢复重力场模型到120阶，一个月的数据形成设计矩阵将花费96小时，这还未包括法方程的形成与解算。如果将来的卫星重力梯度计划GOCE顺利实施，期望恢复重力场位系数到250阶，对应的未知数个数为62 997个，如果所有数据均以双精度保存，法方程矩阵的存储空间要求31.75 G，虽然目前计算机的硬盘存储不再是关键问题，但程序运行需要31.75 G的内存空间，对于目前任何一台单机都无法满足要求，因此无论是从计算时间考虑，还是从内存管理考虑，都必须寻找解决问题的新方法，并行计算技术提供了解决这个问题的唯一途径。

2 卫星重力解算地球重力场的并行化设计分析

利用卫星重力数据解算地球重力场模型引入并行算法的主要目的:在计算规模一定的情况下，尽量缩短计算时间;在给定的硬件设备限制范围内，扩大问题求解的规模。

算法的评价通常用执行该算法所需的时间和所需的计算机内存容量(空间)来评价，即用算法的时间复杂度和空间复杂度衡量其效率和计算难度。由于我们的问题总是针对一定的规模进行，因此对于时间复杂度给予更多的关注。众所周知，同一算法的计算机执行时间与计算机型号、程序语言及程序员的技能等有关，因此，这个时间无法精确度量，我们需要基于算法本身来确定算法的时间复杂度，而不受机型以及这个算法如何编码等因素的影响。时间复杂度简单地定义为:从输入数据到计算出结果所需的时间，记为O(n)。表1给出了3类程序时间复杂度。

表1 三类程序时间复杂度计算Tab.1 Time complexity of three types of program

并行算法设计还需要研究并行程序中数据的相关性。能否将顺序执行的程序转换成语义等价的、可并行执行的程序，主要取决于程序的结构形式，特别是其中的数据相关性。如果在机群上程序P1和P2的数据是彼此相关的，则程序不可能设计为并行结构。通常利用伯恩斯坦准则判断两个程序段能否并行执行。如果用Ii表示程序Pi操作的读入数据，Oi表示程序操作的输出数据，则下列3种情况可以保证程序的并行化设计:

1)I1∩O2=Φ:P1的输入数据与P2的输出数据集不相交;

2)I2∩O1=Φ:P2的输入数据与P1的输出数据集不相交;

3)O1∩O2=Φ:P1与P2的输出数据集不相交。

如果保证了算法中存在不相关的进程，从理论上讲问题的解决可以通过并行程序实现。并行程序是通过并行语言来表达的，通常产生并行语言有以下3种途径:

1)设计全新的并行语言;

2)扩展原有串行语言的语法成分，使其具有并行特征;

3)不改变串行语言，而为串行语言提供可调用的并行库。

最完美的并行语言完全脱离串行语言的束缚，从语言成分上直接支持并行计算，可以使并行程序的书写更方便更自然，相应的并行程序也更容易在并行机上实现。但是由于并行计算至今还没有像串行计算那样统一的冯·诺伊曼模型可供遵循，因此并行机、并行模型、并行算法和并行语言的设计和开发千差万别，没有统一标准，导致设计全新的并行语言实现起来难度和工作量都很大。

对于第二种方法，将对串行语言的并行扩充作为原来串行语言的注释得到新的并行程序，若用原来的串行编译器编译，标注的并行扩充部分将不起作用，若使用扩充后的并行编译器编译，则该并行编译器就会根据标注的要求将原来串行执行的部分转化为并行执行。相对于设计全新的并行语言，此种方法难度有所降低，但仍需重新开发编译器，使其能够支持扩充的并行部分，仍具有相当的复杂度。

对于已有的大量串行程序，最简单的并行化方法是直接加入对已有的并行库的调用，这是一种对原来的串行程序设计改动最小的并行化方法，这样原来的串行编译器也能够使用，不需要任何修改，新的程序也将具有并行计算能力。当前最流行的MPI并行程序设计就属于这种方式。对于这3种并行语言的实现方法，目前最常用的是第三种方法。

由以上分析，我们必须针对重力场恢复算法进行并行处理的可行性研究，寻找其中可以并行计算的阶段，即此程序段间的数据之间存在互不相关性，同时保证所给出的并行程序结构具有最小的时间复杂度。卫星重力观测计算重力场模型可采用动力学法、能量法或加速度法，其核心思想即利用不同的卫星观测数据或其推导值可以得到各种重力观测量，据此建立起与地球重力场模型位系数之间的函数关系，即观测方程，从而可用最小二乘方法形成法方程，直接对法方程系数阵求逆可得位系数最佳估值。对于上述计算过程，经分析可以得出卫星重力场模型解算中通常存在的3种类型并行结构:

1)海量观测数据的并行计算:将读入的观测数据等分地分配到各个CPU，各个CPU协同分别计算设计矩阵，最终通过迭加得到设计矩阵A，即利用并行设计将一个任务分成多个子任务，达到减少计算时间的目的;

2)矩阵与矩阵乘和矩阵与向量乘;

3)线性方程组的求解(包括法方程直接求逆或共轭梯度迭代求解)。

对于后两种并行计算的实现，可以在原有代码中加入调用已有的并行库语句，经过并行编译器编译，就可以实现并行计算，而不需要对原有程序作大的改动。

3 矩阵运算的MPI并行化设计

由分析可以看出，提高重力场解算效率的关键问题之一就是矩阵运算，尤其对于卫星重力数据观测导致的稠密矩阵，主要包括两种运算:矩阵相乘、矩阵与向量乘。由于矩阵与向量乘可以转换为矩阵与一维矩阵乘，因此，本节给出矩阵相乘在GS80并行机上通过调用MPI库的并行化设计。

给出一般性的假定:A为M×N阶矩阵，B为N ×L阶矩阵，C为M×L阶矩阵，即求解矩阵乘积C =A·B。

由于GS80并行机共有8颗CPU，为了保证最大限度地利用计算资源，令程序进程数NPROCS等于8。在通常情况下，矩阵的维数不为8的整倍数，为描述简单，假定M和L均为8的整倍数，则矩阵A、B和C的子块大小分别为MLOC×N，N×LLOC，MLOC×L，A和C按行等分成子块存储在8个进程中，B按列等分成子块存储在对应的8个进程中，其中MLOC=M/8，LLOC=L/8。图1给出了矩阵乘法并行化分块策略。

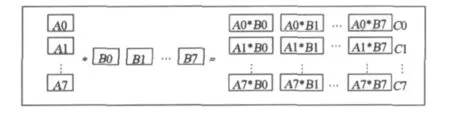
图1 矩阵乘法并行化分块策略Fig.1 Parallel partitioned strategy for matrix multiplication

图1中分块矩阵对应的具体存储方式为:

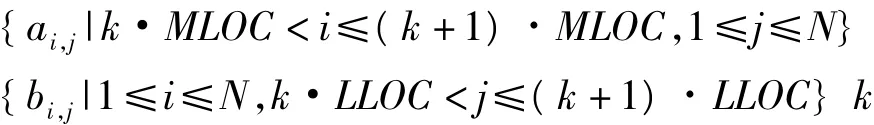
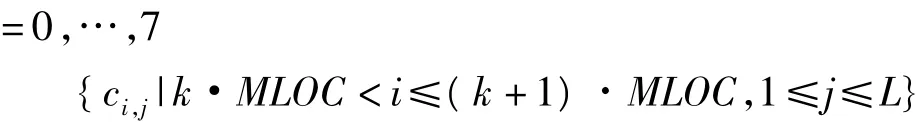
各个矩阵元素分别对应存储在进程k的A、B和C数组中。如果保持矩阵A和C的子块不动，矩阵B的子块在各个进程间循环移动，即可完成矩阵的并行乘法，程序设计算法流程见图2。

为了解程序并行化对计算效率的提高程度，在GS80服务器上安装了MPICH1.2.6版本，它支持所有的MPI-1.2特征和部分的MPI-2的特征，MPICH编译安装成功后，所有MPI并行程序的编译与原先的FORTRAN编译命令参数一致，只是编译器由原先的f77/f90变为mpif77，对应程序的运行需要调用mpirun命令，并且需要指定并行的CPU个数，例如mpirun-np 8 program.bat命令指定使用CPU个数为8颗。表2给出了不同大小矩阵相乘在不同并行进程数目下所花费的时间与每秒百万次浮点运算MFLOPS(Million Floating-point Instruction Per Second)值。

从表2可以看出，对于小运算量，并行算法并不能体现并行的优点，甚至会降低计算速度，这主要是因为数据在总线的传输时间大于CPU的计算时间，但对于大计算量的工作，并行算法将以几何级数提高计算效率(TIME:20s-10s-5s)，同时计算能力也大大增强(MFLOPS:50-100-200)。

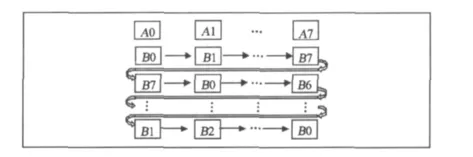
图2 矩阵乘法并行化流程图Fig.2 Flow chart of matrix multiplication in parallel

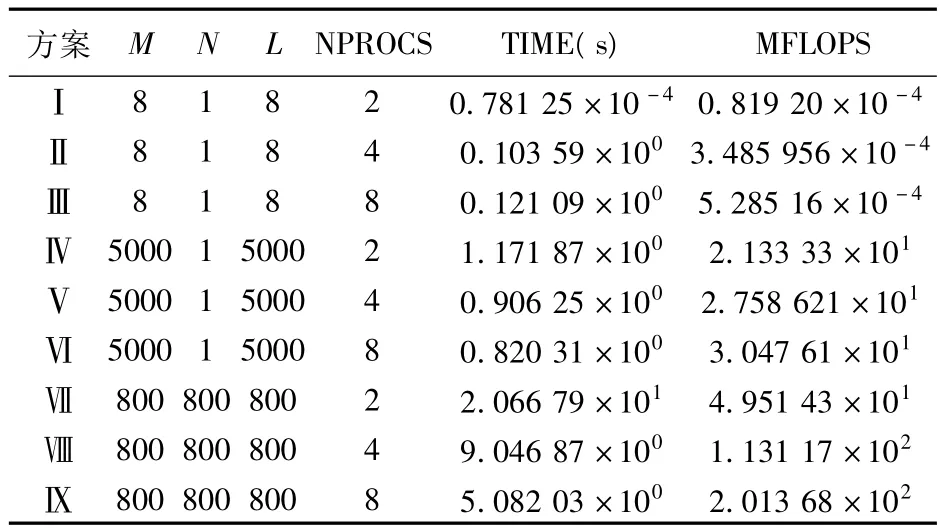
表2 GS80服务器的并行计算效率Tab.2 Parallel computing efficiency of GS80 server

4 最小二乘直接解法并行分析

最小二乘直接解法形式上最为简单，并且能够提供误差估计信息，但由于其对于内存的苛刻要求，使得200阶以上重力场模型位系数在普通微机上的解算陷入困境。除了内存限制外，构建法方程矩阵及其求逆是一项十分耗时的工作，这些不利因素都可以通过并行计算得到解决。

对于最小二乘直接解法的流程，有3个关键的密集型计算任务。第一个是以行形式计算设计矩阵A，第二个是矩阵乘和向量乘分别得到法方程矩阵N和b，最后一个是线性方程系统的求逆。图3给出了最小二乘直接解法流程图。

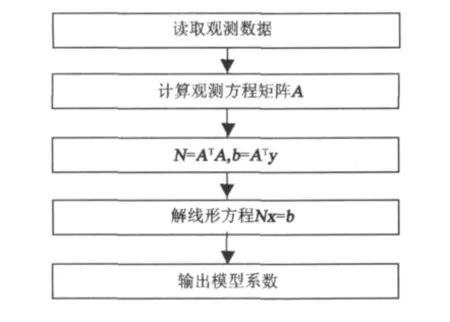
图3 最小二乘直接法流程图Fig.3 Fflow chart of least squares direct method

作为实验算例，给出直接最小二乘算法的耗时，利用16 200个卫星重力扰动位观测，基于扰动位的球谐展开求解50阶重力位系数，程序中涉及的矩阵相乘等的数学运算均直接调用数学函数库，包括Intel MKL、Goto BLAS、BLACS和ScaLAPACK。通过在程序中设置时间断点，获取每一步的计算时间，当仅选取一个CPU时，相当于串行计算，具体耗时为:构建A，耗时0.936 s;构建N耗时12.739 s;构建b耗时0.049 s;解方程耗时0.778 s，总时间耗时14.531 s。从统计结果可以看出，对于直接解最小二乘法，大部分的时间用在计算法方程矩阵N上，构建设计矩阵A和解线性方程系统也需要花费一定的时间。总时间则由观测个数和未知数个数决定，但各部分的时间消耗比例基本保持不变，不随问题的大小而改变。下面分别就OpenMP和MPI两种并行化方法进行详细的对比与分析。

4.1 OpenMP并行化分析

使用的OpenMP并行环境是Intel Fortran自带的，通过在编译命令里增加-openmp参数开启并执行并行运算。从分析和OpenMP的特性可以看出，设计矩阵A，法方程矩阵N和线性方程系统解算3部分工作可以进行并行计算。

对于多核心的CPU，改变默认线程数n的命令是:

BASH环境:export OMP_NUM_THREADS=n

C-Shell环境:setenv OMP_NUM_THREADS=n

解算问题的规模保持不变，分别设置线程数n =1，2，3，4，计算结果如表3所示。为直观表示，图4给出了对比结果。

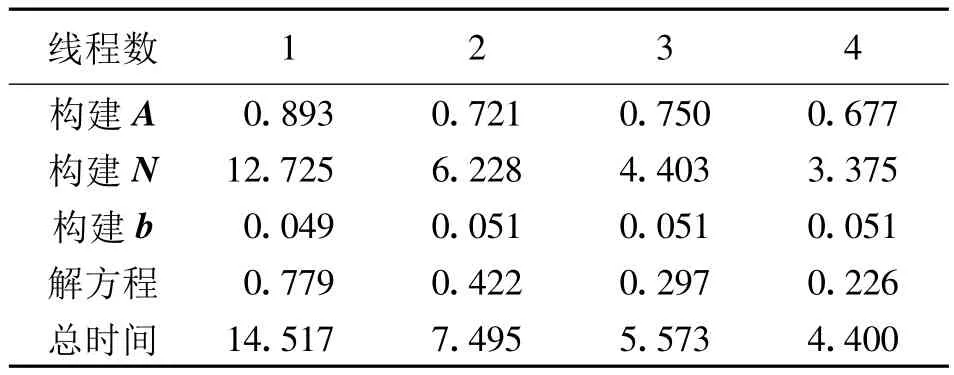
表3 基于OpenMP环境的运行时间(单位：s)Tab.3 Run-time based on OpenMP parallel environment (unit：s)

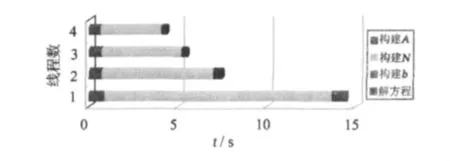
图4 基于OpenMP环境的运行时间Fig.4 Run-time based on OpenMP parallel environment

从图4可以看出，OpenMP的多线程并行计算有明显的效果，尤其对于计算法方程矩阵N，计算时间成比例递减，效果最好;对于计算设计矩阵A和解线性系统也有明显改善。从图4还可以看出，由于除N的计算外，其余几项任务对线程数不敏感，因此当线程数提高到3以上，总的计算时间并不能节约太多。

由此可以看出，基于OpenMP的并行化实现非常容易，只要程序中存在可以被并行化的部分，编译器将自动分析并给出并行化执行方案，用户不需要进行交互操作，也不需要对进程执行进行管理，但是这种方法局限于共享内存构架，只适用于SMP和DSM机器。

4.2 MPI并行化分析

相比于OpenMP线程级并行化，MPI具有更好的扩展性，它属于进程级的并行计算，适合于各种构架，尤其是分布式存储的特点，除了SMP和DSM机器外，还被广泛应用于集群系统。

我们使用的MPI并行环境是Open MPI 1.2.6。它整合了其他MPI的优点，其目标是成为最好的MPI运行库。编译MPI程序需要执行下列命令:

利用上述命令可以自动链接所需要的MPI库函数，程序的执行必须要求下面的格式:

mpirun--hostfile hosts-np n./program

n表示CPU个数或节点数。

基于MPI并行化计算的最小二乘算法的流程为:

1)初始化进程节点;

2)初始化矩阵和对应的内存分配;

3)分布式计算设计矩阵A;

4)分布式计算矩阵相乘和向量乘积;

5)线性方程系统的并行解;

6)参数估值的汇集;

7)退出各计算节点。

其中矩阵相乘和线性方程系统的解由ScaLAPACK的相关子程序计算。解得的结果分别存储在分布式向量b中，输出时，需要将所有节点的系数归集到一个节点上。

解算问题的规模保持不变，分别设置n=1，2，3，4，计算结果列于表4;图5给出了对比结果。

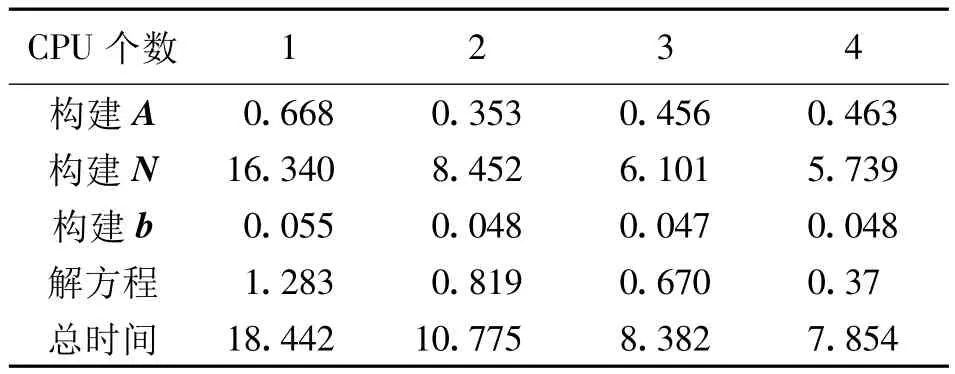
表4 基于MPI并行环境的运行时间(单位：s)Tab.4 Run-time based on MPI parallel environment(unit：s)

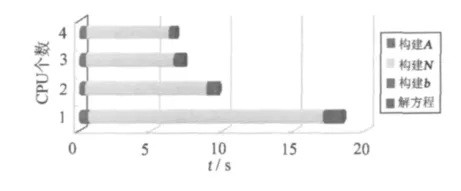
图5 基于MPI并行环境的运行时间Fig.5 Run-time based on MPI parallel environment

从图5可以看出，MPI的多线程并行计算同样有明显的效果，可大大加速法方程矩阵N的生成，对于设计矩阵A，由于处理的问题太小，其计算时间没有成比例的减少，反而随着CPU数目的增多耗时越来越大。

除了上述两种并行化设计外，分布式共享内存(OpenMP+MPI)的并行计算机结合了前两者的特点，是当今新一代并行计算机的一种重要发展方向。

由表5和图6可以看出，相比于OpenMP，MPI由于涉及分布式内存的信息传递，对于这样的小规模运算，并未能表现出优势，相反，其运算速度比OpenMP还慢。

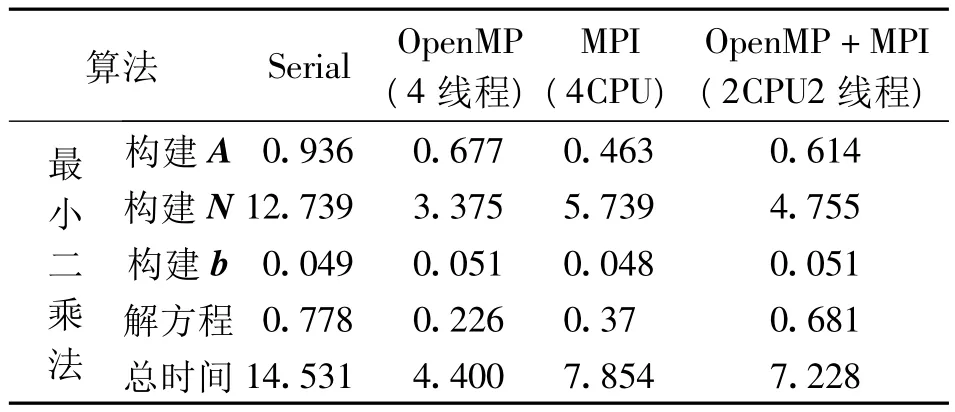
表5 不同计算环境运行时间(50阶)(单位：s)Tab.5 Run-time based on different computing environments(unit：s)

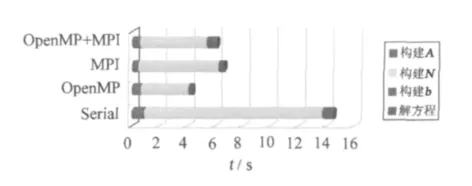
图6 不同计算环境运行时间Fig.6 Run-time based on different computing environments

5 结语

对于卫星重力场恢复解算中涉及的3种类型并行结构可以通过不同并行算法实现，其中海量观测数据的并行计算需要单独设计并行程序，根据CPU的个数决定并行进程的数目，在不同的CPU节点分别计算设计矩阵，完成各个节点计算后再累加求和即可得到设计矩阵A;对于矩阵相关运算和线性方程组的求解，则可以通过MPI库函数的调用实现。通过并行解技术以及超级计算机的使用，海量的卫星重力观测数据处理和更高阶地球重力场模型球谐系数的解算将变得更加容易。与此同时，对于不同的并行算法，需要考虑各自的最优适用范围，利用OpenMP可以简单的实现算法的并行化，对于小规模的计算，其速度要高于MPI并行程序，主要是MPI涉及消息传递，总线速度的快慢对其影响较大;对于循环算法的并行化，最优的选择是采用纯MPI环境，注意避免更多的消息传递，尤其对于较慢的总线界面，例如传统的网络;当需要更少的消息传递时，多线程的MPI程序的效率要远远高于单线程程序。

1 Gropp W，Lusk E and Skjellum A.Using MPI:Portable parallel programming with the message-passing interface［M］.Cambridge，MA:MIT Press，1994.

2 Pail R and Plank G.Assessment of three numerical solution strategies for gravity field recovery from GOCE satellite gravity gradiometry implemented on a parallel platform［J］.Journal of Geodesy，2002，76:462-474.

3 Pail R and Plank G.Comparison of numerical solution strategies for gravity field recovery from GOCE SGG observations implemented on a parallel platform［J］.Advances in Geosciences，2003，1:39-45.

4 Xiao H D and Lu Y.Parallel computation for spherical harmonic synthesis and analysis［J］.Computersamp;Geosciences，2007，33(3):311-317.

5 Xie J.Implementation of parallel least-square algorithm for gravity field estimation［R］.Dept.of Geodetic Science，The Ohio State University，Columbus，Ohio，2005.

6 陈国良.并行计算——结构、算法、编程［M］.北京:高等教育出版社，1999.(Chen Guoliang.Parallel computing— structures，algorithms and programming［M］.Beijing: Higher Education Press，1999)

7 李迎春.利用卫星重力梯度测量数据恢复地球重力场的理论与方法［D］.解放军信息工程大学，2004.(Li Yingchun.Theories and methods of the earth’s gravity field recovery by using of satellite gravity gradiometry data［D］.PLA Information Engineering University，2004)

8 宁津生.卫星重力探测技术与地球重力场研究［J］.大地测量与地球动力学，2002，(1):1-5.(Ning Jinshedng.The satellite gravity surveying technology and research of earth’s gravity field［J］.Journal of Geodesy and Geodynamics，2002，(1):1-5)

9 黄谟涛，等.超高阶地球位模型的计算与分析［J］.测绘学报，2001，30(3):208-213.(Huang Motao，et al.Analysis and computation of ultra high degree geopotential model［J］.Acta Geodaetica et Cartographica Sinica，2001，30 (3):208-213)

APPLICATIONS OF PARALLEL SOLUTIONS TECHNOLOGY IN SATELLITE GRAVITY MEASUREMENT

Nie Linjuan1，2)，Shen Wenbin1)，Wang Zhengtao1)and Jin Taoyong1)

(1)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079 2)Hubei Water Resources Technical College，Wuhan 430070)

The parallel algorithm based on supercomputer for solving the Earth’s gravity field model was investigated.Shared and distributed parallel environment(OpenMPamp;MPI)applying to the least squares method are analysed and compared.Different threads，different node to determine the gravity field model at different levels of time consumption and efficiency are compared with each other.

satellite gravity;parallel computing;geopotenial model;OpenMP;MPI

1671-5942(2012)02-0064-06

2011-08-13

国家自然科学基金(41074014);湖北省高等学校青年教师深入企业行动计划项目(XD2010461);教育部博士点新教师基金(200804861022)

聂琳娟，女，博士生，讲师.主要从事大地测量专业理论方法的教学与科研工作.E-mail:ljnie@whu.edu.cn

P223

A