基于MUSIC算法的MIMO雷达的角度估计

付 翔， 张小飞

（1.南京航空航天大学 电子信息工程学院，南京210016；2.滁州学院 机电学院，安徽 滁州 239000）

基于MUSIC算法的MIMO雷达的角度估计

付 翔1，2， 张小飞1

（1.南京航空航天大学 电子信息工程学院，南京210016；2.滁州学院 机电学院，安徽 滁州 239000）

多输入多输出（Multiple－Input Multiple－Output：MIMO）雷达利用多天线发射互相正交的信号，可以实现灵活的发射分集设计，具有高分辨率的空间谱估计性能。为降低计算的复杂度，提升信噪比高时信号的性能，文章基于MUSIC算法对双基站雷达信号的到达角与发射角作相应估计，结合优化方法和误差准则，对不同参数条件下的该算法作了仿真分析和综合比较。结果证明了该算法的有效性。

多输入多输出雷达；角度估计；多重信号分类

MIMO技术在无线通信中技术的成熟，EranFishler等人在2004年引入此项技术提出 MIMO雷达的概念［1］。MIMO雷达可以灵活地采用新一代雷达系统的高带宽、双程数字波束合成和波形分集技术。可克服雷达反射截面积起伏的影响，提高对空中目标的检测能力，具有高分辨率的空间谱估计性能［2～4］。现今因为种种因素 MIMO雷达的角度估计性能并不十分理想，文献［5］主要研究了MUSIC［6］算法在 MIMO 雷达中的 DOA 估计［7－13］性能，但在分辨相近目标时受到一定的限制，因此需要进一步研究提高MUSCI算法在MIMO雷达中的分辨力。文献［14］提出一种高效率的估计DOA的算法，该算法利用均匀线阵，MUSIC算法利用谱峰搜索，减小了运算量，有一定的进步。文献［15］的算法将二维搜索降维为两个一维搜索，性能比计算复杂度高的二维MUSIC算法略好。本文在前人基础上通过矩阵重构，运用MUSIC算法和求根MUSIC算法对MIMO雷达进行角度估计。仿真表明信噪比越高，谱峰越尖锐，该算法性能越好。

1 MIMO雷达接收信号模型

考虑一个包含M个发射天线和N个接收天线的基本MIMO雷达系统，并且发射和接收阵列都是均匀线阵（Uniform Linear Array，ULA），天线间隔均为半波长。我们假设有K个目标，那么接收端匹配滤波器的输出可以表示如下：

其中，θK，φK是第k个目标的发射和到达角；B∈CL×K包含了K个目标和L次采样的幅度和相位，其中相位受到多普勒频移的影响，幅度受到反射波的影响；ar（φk）⊗at（θk）是第k个目标发射和接收向量的Kronecker算子，那么信号模型可以被描述成：

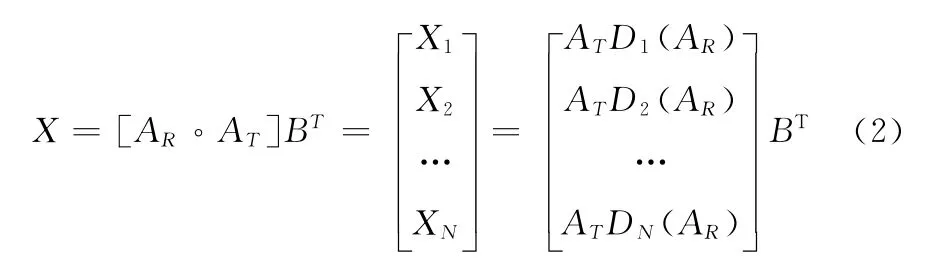
其中AT＝［at（θ1），at（θ2），…，at（θK）］∈CM×K和AR＝［ar（φ1），ar（φ2），…，ar（φK）］∈CM×K是发射方向矩阵和接收方向矩阵。AR◦AT是Khatri－Rao算子，Dm（.）是取相关矩阵的第m行组成一个对角矩阵。因此，X的第n个块可以表示为：

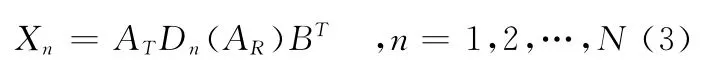
在噪声的影响下，信号模型变成~Xn＝ATDn（AR）BT＋Vn，n＝1，2，…，N，其中Vn是第n个接收信号上的噪声。

2 MUSIC算法

2D－MUSIC算法中进行谱峰搜索需要用到二维搜索，因此计算复杂度大幅度提高，为了避免这个缺陷，在此尝试使用MUSIC算法。MUSIC算法需要分别进行两次搜索，通过接收信号估计DOA和DOD。由于MIMO雷达的接收信号不满足MUSIC算法的使用条件，因此运用这种方法进行角度估计时，在保证接收和发射阵列矩阵信息不被破坏的前提下，需要对接收信号矩阵进行矩阵重构，从而得到我们想要的结果。

2.1 算法推导

接下来将详细推导如何用该算法进行矩阵重构，从而准确地估计DOA。文章中使用到的MIMO雷达模型均是（2）处构建的模型。

MUSIC算法要求所处理的信号在理论上具有X＝AS的形式，而实际接收到的信号是X＝［AR◦AT］BT，显然，要想准确地估计阵列参数，必须是待处理信号满足X′＝ATS的形式。

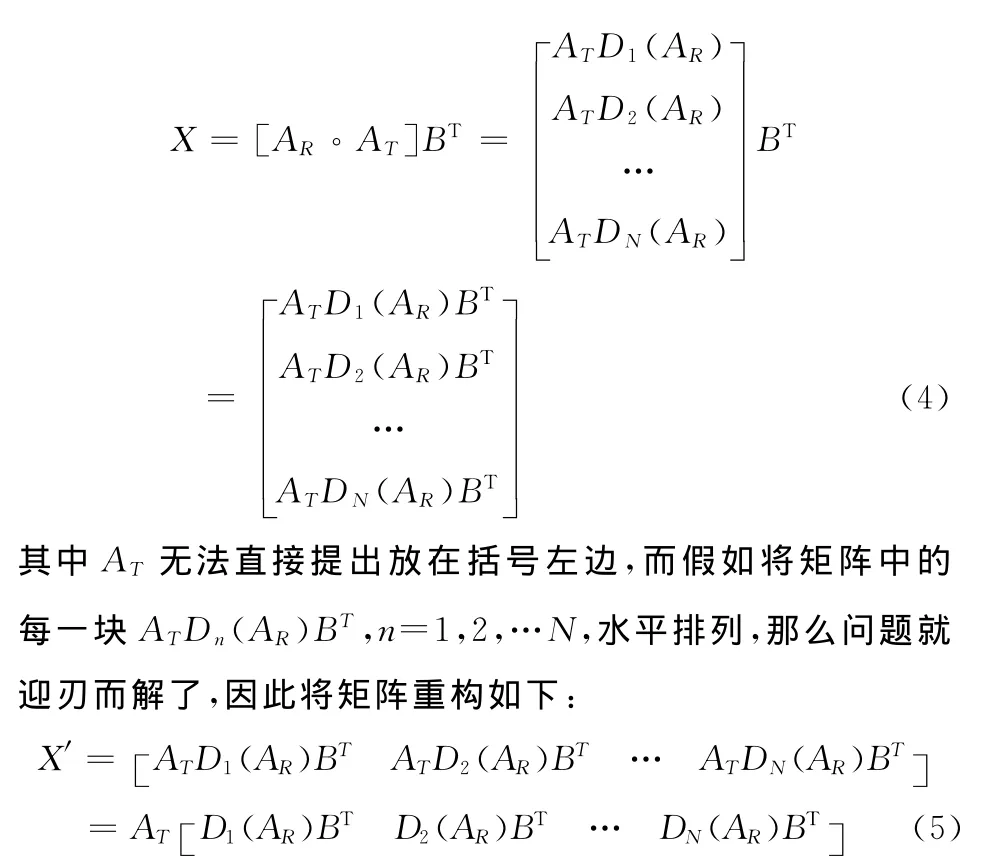
然后将X′代入MUSIC算法，即可准确地估计出DOD。

同理，对于估计DOA，也必须构造一个矩阵，使之满足X″＝ARS′的形式。直接根据接收信号无法获得，需要一个复杂的矩阵重构才能得到所需的形式。在研究过程中，由AT◦AR和AR◦AT的关系得到启发，由接收信号成功地构造出了X″＝ARS′，从而准确地估计了接收角。定义˙X为：

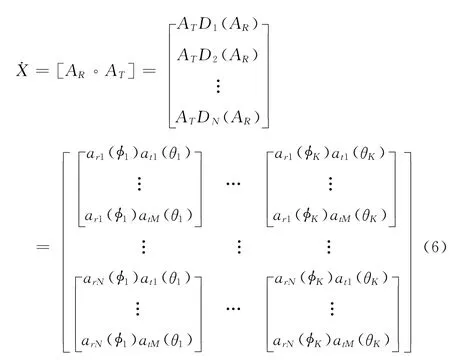
其中arn（φk）是ar（φk）矢量中的第n个元素；atm（θk）是at（θk）矢量中的第m个元 素.

令重构后的矩阵为¨X，则：

将˙X的第1，1＋M，1＋2M，…，1＋（N－1）M行移至¨X的第1至N行；

将˙X的第2，2＋M，2＋2M，…，2＋（N－1）M行移至¨X的第1＋N至N＋N行；

将˙X的第M，M＋M，M＋2M，…，M＋（N－1）M行移至¨X的第1＋（M－1）N至N＋（M－1）N行；于是得到¨X为：

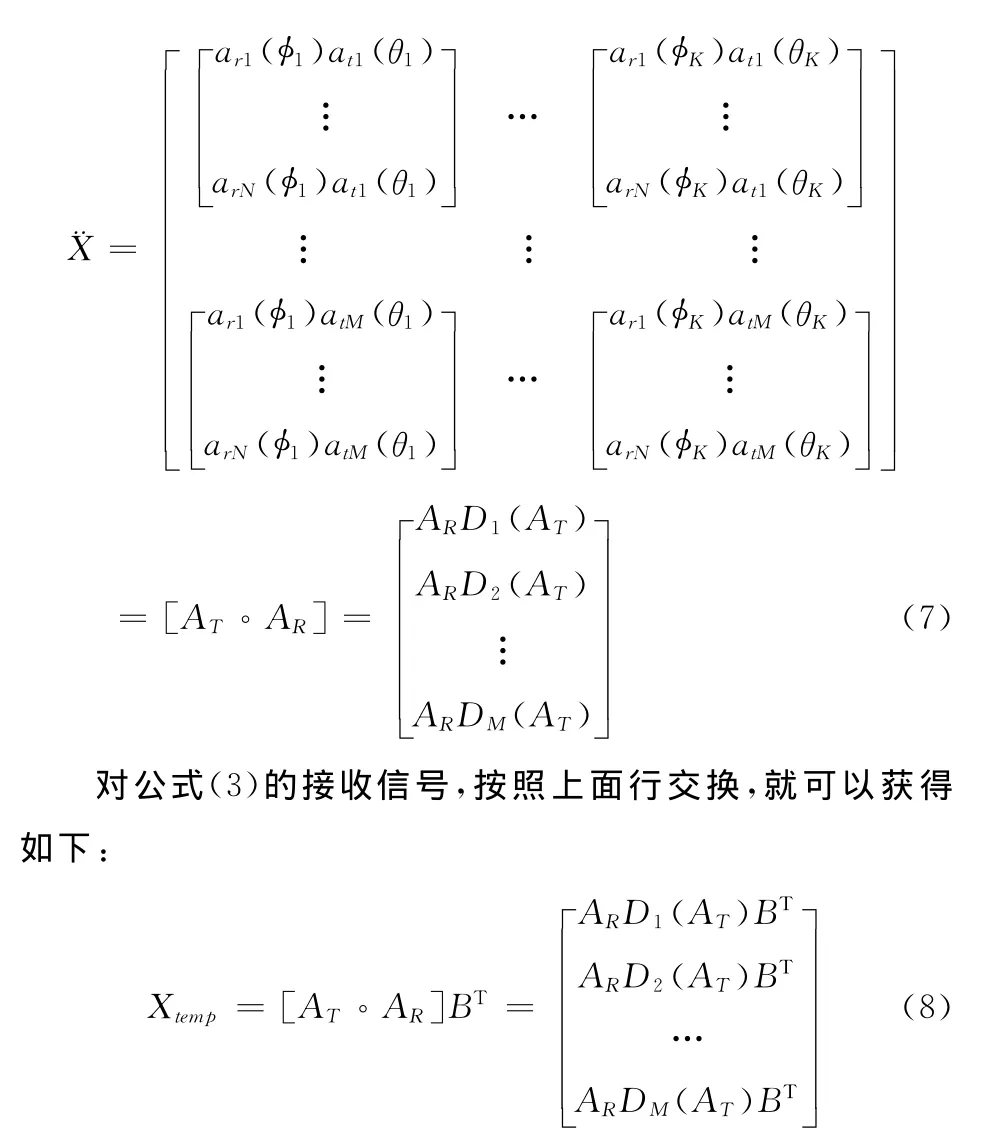
因此，将接收信号按照上述方法重构，可以类似的得到一个矩阵Xtemp，再Xtemp将按照之前估计DOD的方法再进行一次重构，就可以得到X″＝ARS′，然后代入 MUSIC算法即可得到准确地估计DOA结果。

2.2 算法仿真

采用MUSIC算法通过接收信号估计MIMO雷达的DOD和DOA。快拍数L＝100，目标数K＝3，发射天线数M＝8，接收天线数N＝8，假设发射角为10°，20°，30°，到达角为15°，25°，35°，信噪比分别为15dB和25dB，如图1和图2所示。

通过图1和2我们可以清楚地看到MUSIC算法能够成功地将MIMO雷达的发射角和到达角估计出来，而且信噪比越高，谱峰越尖锐，性能越好。

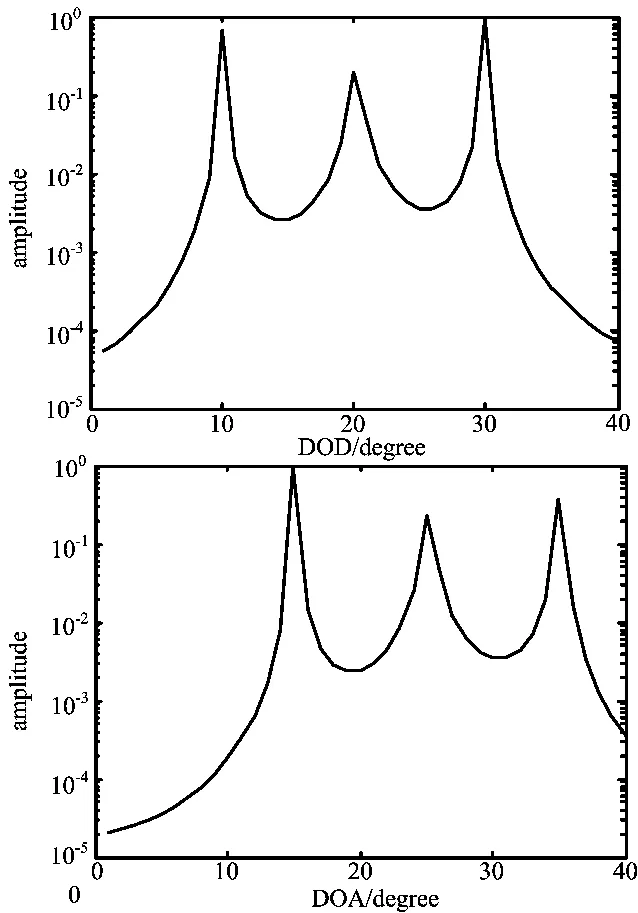
图1 信噪比为15dB时MUSIC算法的估计性能

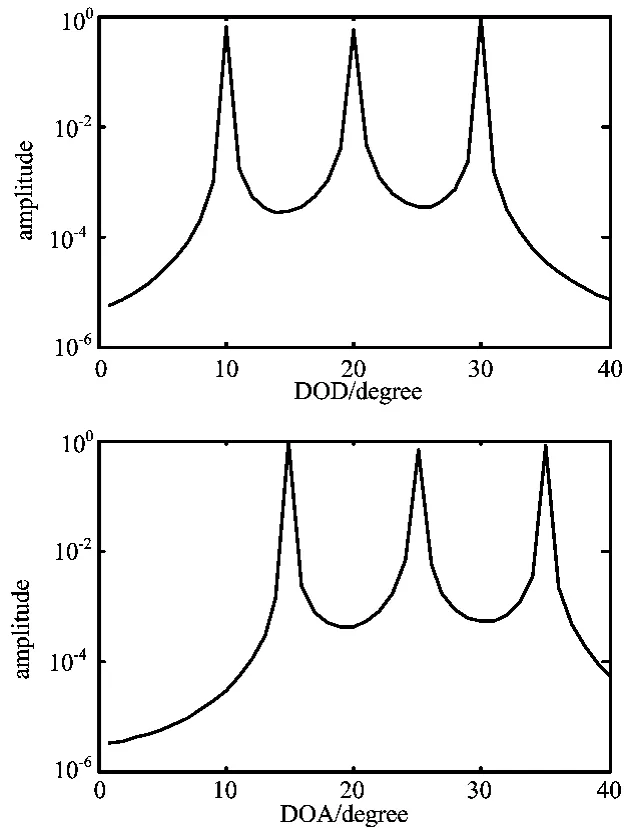
图2 信噪比为25dB时MUSIC算法的估计性能

为了进一步研究MUSIC算法的精度，下面计算MUSIC算法的RMSE（Root Mean Square Error求根均方误差）。

计算RMSE采用如下公式：

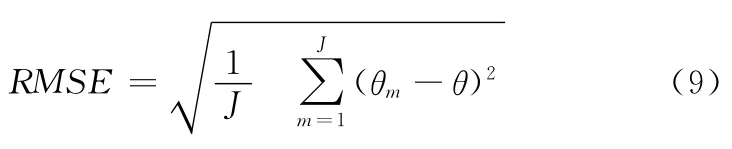
其中J是仿真次数，θm是第m次仿真得到的发射角／到达角的估计值，θ是发射角／到达角的精确值。

采用公式（8）计算MUSIC算法的RMSE。快拍数L＝50，目标数K＝3，发射天线数 M＝8，接收天线数N＝8，假设发射角为10°，20°，30°，到达角为15°，25°，35°，让信噪比从0dB变化至20dB进行1000次仿真，如图3所示。

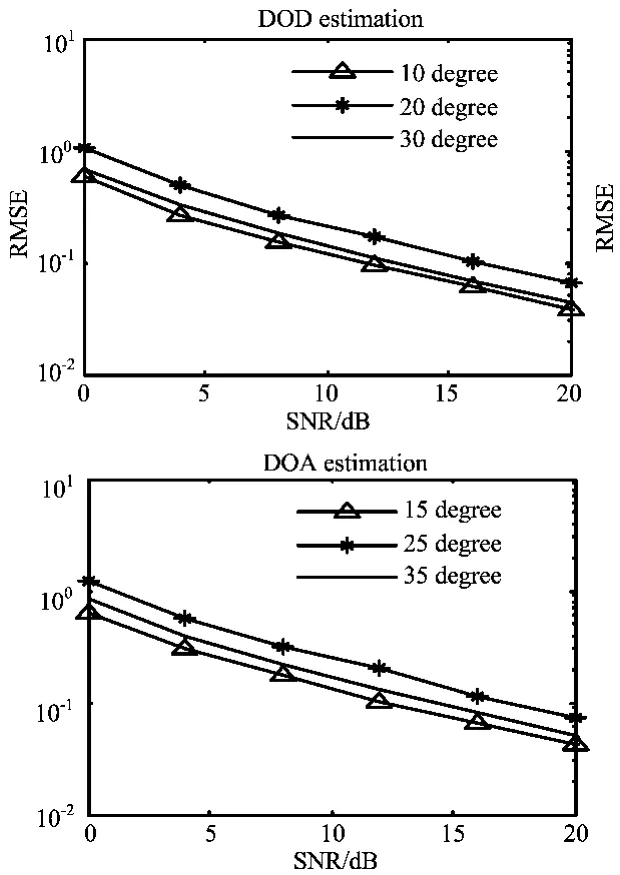
图3 不同信噪比情况下MUSIC算法的求根均方误差

通过观察图3我们可以看到，随着信噪比的提高，MUSIC算法的求根均方误差也越小，估计性能越好。

3 结束语

本文详细讨论了MUSIC算法是如何应用在MIMO雷达的角度估计上的，并且应用不同的系统参数进行了仿真和比较。传统的2D－MUSIC算法需要进行二维谱峰搜索使得运算量过大，本文算法在此基础上，仍然进行谱峰搜索但加以改进，需要两次一维搜索即可，使复杂度大大降低。由于在高信噪比时候，此算法仍具有良好的性能，因此本文算法在实际应用方面具有很大的优越性。

［1］E.Fishler，A.Haimovich，R，S.Blum，et al.MIMO radar：An idea whose time has come［C］.Proceedings of the IEEE Conference on Radar［C］.Philadelphia，Pennsylvania USA：IEEE Press，2004：71－78.

［2］Tabrikian J，Bekkerman I.Transmission diversity smoothing for multi－target localization ［radar／sonar systems］［A］.IEEE International Conference on Acoustics，Speech，and Signal Processing（ICASSP’05）［C］.Philadelphia，Pennsylvania USA：IEEE Press，2005：1041－1044.

［3］Luzhou Xu，Jian Li.Iterative generalized－likelihood ratio test for MIMO radar［J］.IEEE Transactions on Signal Processing，2007，55（6）：2375－2385.

［4］Lehmann N H，Fishler E，Haimovich A M，et al.Evaluation of transmit diversity in MIMO radar direction finding［J］.IEEE Transactions on Signal Processing，2007，55（5）：2215－2225.

［5］王艳苹，张志斌，陈娟，等.MIMO雷达DOA估计方法分析［J］.电子科技，2010，23（3）：76－80.

［6］R.O.Schmidt，Multiple emitter location and signal parameter specetral estimation ［J］.in Proc.RADCS plectrum Estimation Workshop，oct1979，or IEEE.Trans，AP1986，34（3）：276－280.

［7］张贤达，保 铮.通信信号处理［M］.北京：国防工业出版社，2000.

［8］魏 平.高分辨阵列测向系统研究［D］.电子科技大学，1996

［9］刘德树.空间谱估计及其应用［M］.安徽：中国科技大学出版社，1997.

［10］Thng，A.Cantoni，and Y.H.Leung.Derivative constrained optimum broad－band antenna array［J］.IEEE Trans.Signal Processing，1993，41（7）：2376－2388.

［11］J.W.R.Griffiths.Adaptive array processing：a tutorial［J］.IEEE Proc，1983，130：3－10.

［12］赵永波，刘茂仓，张于宏.一种改进的基于特征空间的自适应形成算法［J］.电子学报，2000，28（6）：16－18.

［13］张林让.自适应阵列处理稳健方法研究［D］.博士论文 西安电子科技大学，1998.

［14］Yongbo Zhao，Penglang Shui，Hongwei Liu.Computationally Efficient DOA Estimation for MIMO Radar［C］.Image and Signal Processing，2009.CISP＇09.2nd International Congress on.2009：1－3.

［15］Zhang Xiaofei，Xu Dazhuan.Angle estimation in MIMO radar using reduced－dimension capon［J］.IET Electronics Letters，2010，46（12）：860－861.

Angle estimation for MIMO Radar System based on Multiple Signal Classification Estimation Algorithms

Fu xiang，Zhang xiaofei

Multiple－input－multiple－output（MIMO）radar，which utilize multiple antennas to simultaneously transmit orthogonal signals，offers flexible design of transmit diversity and high resolution of spatial spectrum estimation.To reduce the calculating complexity and enhance the signal quality at high SNR（Signal to Noise Ratio），a direction of departure（DOD）and direction of arrival（DOA）estimation algorithm is proposed in bistatic MIMO radar based on MUSIC estimation algorithm.Combined with optimization method and error criterion，simulation analysis and comprehensive comparison has been made for this algorithm in different parameter condition，and the results demonstrate its effectiveness and robustness.

Multiple－input multiple－output（MIMO）radar；direction of departure（DOD）；direction of arrival（DOA）；Multiple Signal Classification

TN919

A

1673-1794（2012）02-0039-03

付 翔（1984－），女，硕士研究生，研究方向：信号处理；张小飞（1977－），男，教授，研究方向：移动通信技术、通信信号处理、阵列信号处理。

安徽省高校省级科学研究项目自然科学一般项目（KJ2012Z279）；滁州学院科研项目（2011kj018B）

2012-01-26