自由网平差的近似坐标影响研究
周 蕴
(郑州市规划勘测设计研究院,郑州450052)
1.引言
经典平差中,都是以已知的起算数据为基础,将控制网固定在已知数据上。如水准网必须至少已知网中某一点的高程,平面网至少要已知一点的坐标、一条边的边长和一条边的方位角。当网中没有必要的起算数据时,我们称其为自由网,网中没有起算数据时的平差方法,即自由网平差[1,2]。
边角网中,选取的参数往往是待定点的坐标,而观测值一般为方向值、角度值或边长,因而观测值和参数之间建立的关系均是非线性函数[3]。如果不给出近似坐标,观测方程就无法线性化,误差方程就无法列出。因此如何选取近似坐标,假定自由坐标在自由网平差中的可靠性是个不容忽视的问题。本文对自由网平差中选用不同近似坐标对平差计算结果的影响进行了详尽的分析和研究。
2.自由网平差原理
函数模型:

随机模型:

其中R(A)=t-d,d为秩亏数,在最小二乘原则下,求得法方程为:

式中R(N)=R(A)=t-d。由于N是奇异的,即法方程是相容方程,它可以有无数解。因此,附加一个最小范数条件:

从而得到法方程的唯一解:

(5)式中,N+为N的伪逆,上述平差方法即为秩亏自由网平差。
3.近似坐标的计算
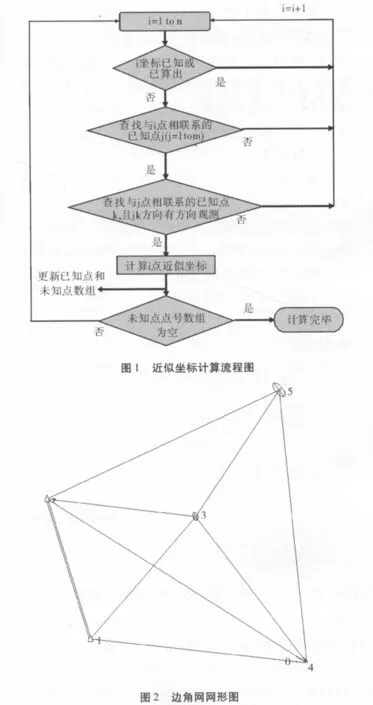
考虑到变形监测的边角网大多为边角同测网,在计算近似坐标时可采用极坐标法。极坐标法的基本思路:若存在已知方位角,首先判断该方位角的起点是否是已知点A,终点是否是所求的待定点P,如果是,搜索边长AP即可按极坐标公式计算坐标;若没有已知方位角或其终点不是P,则搜索与P有方向观测的已知点A,再由A搜索另一个已知点B,且A到B有方向观测值,于是可求出AP的方位角,再搜索AP的边长观测值,由极坐标公式即可计算P点的坐标。坐标计算的流程图如图1所示:
4.不同近似坐标得到的平差结果比较
为验证不同近似坐标对平差结果的影响,本文采用的数据为pad2002边角网算例(原网形如图2)并选取如下3个参考系:
1)参考系:原点为1号点,1-3方向方位角为0
2)参考系:原点为1号点,1-4方向方位角为0
3)参考系:1 号点(31250.250,11500.410),2号点(33256.570,10900.840)
对3个参考系,采用上述计算方法计算近似坐标并进行自由网平差,结果见表1、表2。
4.1 观测值改正数分析

表1 边长平差值改正数
由表1,2可知,边长改正值相差最大为0.06 mm,方向改正值相差最大为0.02s。在误差允许的范围内,可以认为改正数是相同的。
4.2 三种不同近似坐标参考系迭代次数
参考系1:5
参考系2:4
参考系3:3
可见采用不同的参考系,需要迭代的次数是不完全相同的,这和坐标近似值的准确程度有关。

表2 方向平差值改正数
4.3 三种不同近似坐标参考系的控制网网图及误差椭圆

图3 控制网网图及误差椭圆(参考系1)

从图3、图4、图5三幅不同近似坐标参考系的控制网网图及误差椭圆图可以明显看出,不论是控制网的网形,还是误差椭圆的方向和形状,都仅仅是旋转。从改正值和误差椭圆的分析,可以看出控制网选用不同的近似坐标系统进行平差有相同的改正数和相同的网形及误差椭圆。
5 结束语
本文研究了自由网平差中选用不同参考系的近似坐标,因近似坐标的准确度,对平差迭代次数有一定影响,而平差数据的观测值的平差值,以及平差后的点位坐标并不影响。表明在变形监测数据的严密平差中(迭代次数足够),采用不同的近似坐标对平差结果的影响几乎可以忽略。
[1]朱建军,贺跃光,曾卓乔.变形测量的理论与方法[M].长沙:中南大学出版社,2004.
[2]陶本藻.自由网平差与变形分析[M].武汉:武汉测绘科技大学出版社,2001.
[3]武汉大学测绘学院测量平差学科组.测量平差基础[M].武汉:武汉大学出版社,2003.
——兼谈参考系与坐标系的关联关系

