无黏结材料颗粒流模型的宏细观参数关系研究

颜 敬，曾亚武，高 睿，杜 欣

(武汉大学土木建筑工程学院，武汉 430072)

1 研究背景

离散单元法(如PFC2D/3D，UDEC/3DEC)是近些年来兴起的一种新的岩土工程数值计算方法。该方法一般按其用途，又可以分为细观离散元和宏观离散元。前者着重于处理数目众多、具有不连续特征的接触面或点的问题，例如破碎岩体中的破裂面、砂土中的接触面(点)、散体材料中粒子之间的接触面(点)等;后者则主要解决规模相对较大的不连续面，如断层、节理、结构与基础之间的结合面等引起的一系列问题等［1－4］。PFC(Particle Flow Code)是在岩土界著名学者Peter Cundall院士主持下采用细观离散元理论(又称为粒子流或者颗粒流理论)开发的一套商业数值计算软件，可以广泛地应用于研究细观结构控制的问题，具有很大的发展潜力。

ITASCA公司开发的PFC系列软件，作为细观离散元软件平台，具有2个最基本的特征［2－4］。

(1)允许颗粒发生有限的位移和转动，颗粒之间允许完全脱离;

(2)程序在计算过程中能够自动辨识新的接触。该理论的核心思想是采用最基本的单元——粒子和最基本的力学关系——牛顿第二定律来描述介质的复杂力学行为，而无需事先确定材料的宏观本构，模型介质的本构特征将由其内部颗粒之间状态特征的变化体现出来，颗粒间接触的破坏与发展意味着介质整体力学特性由线性向非线性转化。

PFC的这种理念导致其在很大程度上不同于其他连续和非连续介质力学理论方法与程序，其中的一个关键问题就是:介质的宏观基本物理力学特征不能通过直接赋值的形式实现，只有颗粒的几何特性和颗粒间接触的细观力学参数可以赋值，并且这些参数大都无法测量，但介质的宏观力学特征又取决于颗粒的这些基本特性，一旦改变了这些基本特性，就意味着改变了介质的宏观力学性质。

正是由于PFC具有这些特点，在投入工程计算之前，必须利用同样的粒子几何参数建立简单的室内试样模型，并对这些试样分别赋予不同的细观力学参数进行一系列的数值试验，以获得试样的宏观力学参数，并将这些测试结果与实际工程相应的宏观参数值进行比较，选择对应的细观力学参数作为实际模型计算用参数，即要进行一个复杂的细观力学参数标定工作。这个过程与地质力学材料模型试验前期工作中选择和配制模型材料的配合比非常类似［2］。但由于宏观层次和细观层次的参数众多，盲目调试极有可能事倍功半，且极难寻找一个明确的数学模型来表征二者之间的关系，目前采用最多的方法就是变量控制法，即保持某些细观参量不变，改变其他参数取值，探究介质宏观特性的演化规律，例如国内外学者 S.Utili和R.Nova［5］，C.Wang，D.D.Tannant和P.A.Lilly［6］，Geng Yan，Yu Hai-sui和McDowell Glenn［7］，同 济 大学 周 健［8］、Chengbing WANG 和Hehua ZHU［9］，长江科学院李耀旭、王新和丁秀丽［10－11］等都开展了相关的研究工作。

本文拟在前人研究的基础之上，以某无黏结颗粒材料为例，利用正交试验方法设计试样并在不同侧压下进行双轴试验，以探求细观参数不同组合对介质宏观特性的影响，从而避免控制变量法固定某些参数的局限，更加科学地分析细观参量对介质宏观特性影响的敏感程度，并进一步地利用人工神经网络实现两个层次参数间的互演，以供PFC模型进行实际岩土工程计算时参考。

2 正交试验设计

在实际生产和科学研究中，往往需要通过一定的试验来获取一些试验数据，并对这些数据进行科学分析和数学处理，以帮助人们找出问题的主要矛盾及其间的相互关系，明确问题的内在规律，从而寻求问题的解决办法。对于多因素影响的试验，如果采用完全组合将会导致试验次数急剧增加且试验结果整理困难，而正交试验可以用最少的试验次数反映比较全面的情况，并带有充足的变异信息，可以反映不同因素水平组合对结果的影响［12］。

本文以无黏结材料中颗粒的法向刚度kn、刚度比kn/ks(法向与切向刚度之比)、摩擦系数f、平均半径Rm这4个细观参数进行3水平正交设计(依正交表L934，文献［12］)，形成9 类试样，具体见表1。

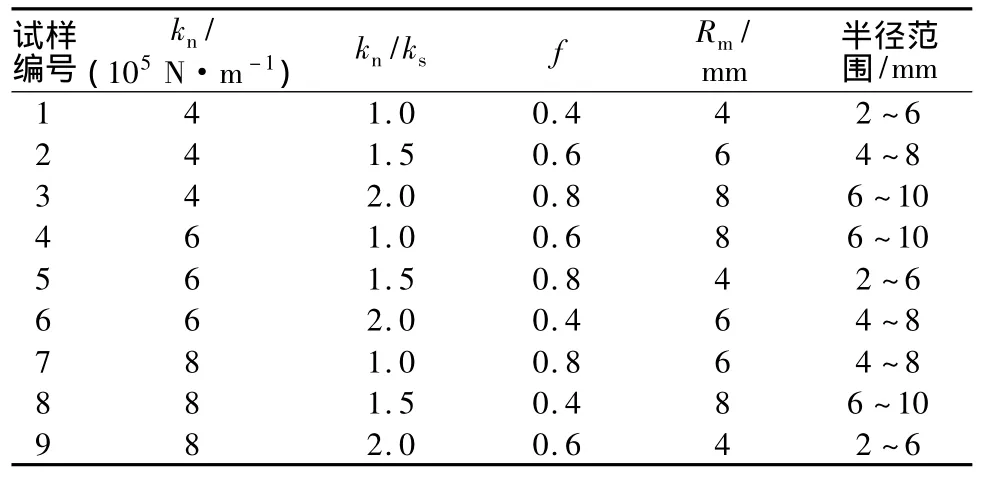
表1 试样设计Table 1 Orthogonal designs for the samples

3 PFC双轴试验

PFC2D软件用4个墙体限制试样形状为矩形，顶墙和底墙模拟加荷板，左墙和右墙模拟试样侧限。在数值试验过程中，通过指定顶板和底板的速度施加轴压，采用平面应变控制式加载，而左右墙体的速度均由数值伺服器自动控制以保持侧压恒定(图1)，具体试验原理见文献［3］。本文选取试样大小为300mm×600mm，孔隙率取为0.1。

试样的应力状态通过边墙的平均接触应力表示(见图2)，即

式中:nc表示与墙体接触的颗粒个数;Fi表示接触集中力;ld是墙体面积，l为墙体有效长度，d表示沿纵向的厚度(一般取单位厚度)。

图1 试验装置Fig.1 Testing device

图2 颗粒-墙体接触Fig.2 Particle-wall contact

依据PFC使用手册，试样的应变状态依照下式进行计算(大应变模型)，即

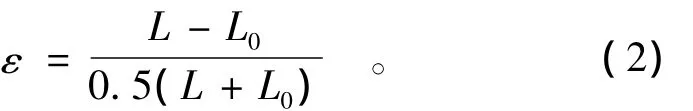
式中:L为变形后的长度;L0为变形前的长度。

体积应变为x，y方向应变之和，即

若侧压为σc，轴向主应力和偏差应力分别为σa和σd，则有弹性模量和泊松比为:

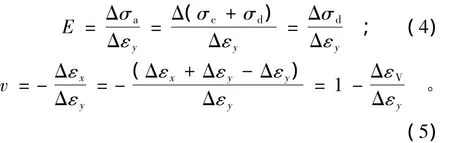
本文侧压分别取10，15，20 kPa，记录每一个试样在3种侧压下的偏应力－轴应变曲线、体应变－轴应变曲线、破坏偏差应力，测试结果见表2。

4 数值试验结果整理与分析

4.1 变形参数E，v

通过27次双轴试验，发现偏应力－轴应变曲线均表现为图3的特征，在原点附近加载曲线可以近似为一条直线，介质呈现线弹性响应，之后进入非线性阶段，达到峰值强度后破坏。依照每一次试验的记录，计算试样在线性阶段的弹性模量和泊松比(初始弹性模量和泊松比，即变形参数，见表3)，并进行统计分析(见表4)。

表2 破坏偏差应力Table 2 Maximum deviatoric stresses kPa

图3 应力-应变曲线Fig.3 Stress-strain curve

表3 弹性模量与泊松比Table 3 Elastic moduli and poisson’s ratios

表4 弹性模量和泊松比的统计分析Table 4 Statistic analysis of elastic moduli and poisson’s ratios

观察试验结果可以发现:在一定范围内，侧压应力不同，试样的弹性模量和泊松比略显差别，但是起伏不大，极差与平均值的比值均在10%以内，即可以用均值表示它们的大小，而无需严格考虑侧压应力的变化。

按照正交试验的结果分析方法［12］，可以分析各个细观参数取值水平对该种材料弹模和泊松比的影响，形成图4和图5，并以弹模为例给出数据的处理过程，见表5和表6，泊松比和下文摩擦角的处理与此类似。

图4 细观参数取值对弹性模量的影响Fig.4 The influence of particle mesoscopic parameter on elastic modulus

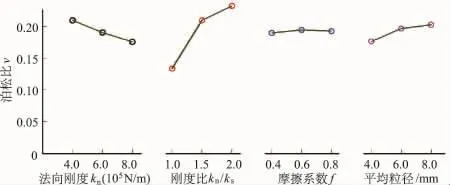
图5 细观参数取值对泊松比的影响Fig.5 The influence of particle mesoscopic parameter on poisson’s ratio

表5 各因素水平试样的弹性模量Table 5 Analysis of elastic moduli of the level of each factor

分析图4、图5、表5和表6可以得出结论:

(1)法向刚度与弹性模量呈现显著的正相关关系，刚度比增大即切向刚度减小可以降低弹性模量。颗粒的摩擦系数和平均粒径对弹模的影响较小。

(2)极差R的大小，反映了试验中各因素作用的大小，极差大表明该因素对指标的影响大。对于弹性模量而言，各因素作用由强到弱排序为:法向刚度、刚度比、平均粒径、摩擦系数。

(3)颗粒刚度在法向和切向的大小差异(刚度比)是影响泊松比的最主要因素，刚度比越大，介质体在宏观上的泊松比就越大。

(4)颗粒法向刚度的增加和粒径的减少可以导致泊松比减小，颗粒摩擦系数对泊松比几乎没有影响。

(5)对于泊松比而言，各因素作用由强到弱排序为:刚度比、法向刚度、平均粒径、摩擦系数。

表6 弹性模量统计分析Table 6 Statistical analysis of elastic moduli kPa

4.2 强度参数φ

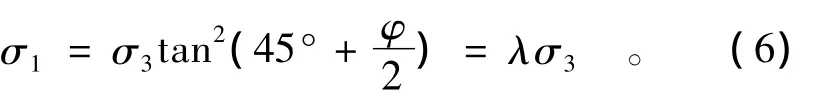
对于无黏结的颗粒材料，根据摩尔库仑强度理论，达到破坏极限时，大小主应力应满足其中内摩擦角度σ3－σ1平面上破坏点应该在一条过原点的直线上，将试验结果绘成曲线，见图6，可以观察到试验结果基本满足这一规律，故可认为在一定应力水平下摩尔库仑强度理论成立且用方程σ1=λσ3进行最小二乘回归可以得到内摩擦角，通过进一步分析可以得出细观参数对内摩擦角的影响(见图7)。

图6 试样破坏时的σ1-σ3关系Fig.6 Relation between σ1 and σ3 when samples fail

(1)内摩擦角与颗粒摩擦系数呈现显著的正相关关系，法向刚度的增加可以适当增加内摩擦角。

(2)对于内摩擦角而言，各因素作用由强到弱排序为:摩擦系数、法向刚度、刚度比和平均粒径。

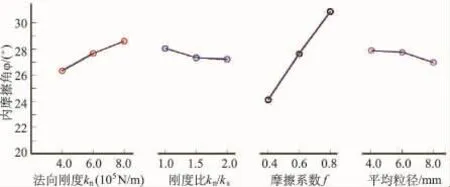
图7 细观参数取值对内摩擦角的影响Fig.7 The influence of particle mesoscopic parameter on internal friction angle

4.3 宏细观参数匹配调整原则

在进行实际岩土工程计算时，要求实际物理试验测试出的介质宏观参数与PFC数值试验测试出的介质宏观特性参数尽可能的一致，这就需要合理调整颗粒流模型的细观参数，如果盲目调试则极有可能事倍功半。根据上面的分析，针对本文讨论的无黏结颗粒材料，可以得到一些基本的调整原则。

(1)仅增大(减小)颗粒摩擦系数可以使内摩擦角增大(减小)，而保持介质弹性模量和泊松比基本不变;

(2)增加法向刚度的同时，增加刚度比，可以提高介质体的弹性模量，且保证内摩擦角基本不变;

(3)保持法向刚度不变，增加刚度比，可以增大介质体的泊松比，且保持弹性模量和内摩擦角度基本不变;

(4)在一定粒径范围内，改变颗粒的大小对宏观参数的影响十分有限;

(5)在处理问题时，应该抓住主要矛盾，将逼近主要宏观参数作为调整目标，而适当放宽对其他参数的模拟要求。

5 宏细观参数间的智能互演

利用人工神经网络［13］的非线性、动态性与鲁棒性的特点，以正交试验结果为训练样本(9个)，建立宏观细观参数之间的相互映射，即互演机制，以实现2个层次参数间的相互预测。在Matlab的平台上，自编程序构建3层BP网络系统。

5.1 正演计算

建立列向量之间的映射关系:

训练形成网络net1，并测试得出(试样粒度分布为3～7mm)

将细观参数输入PFC双轴试验程序以检验预测结果的正确性，得到表7。将破坏时的(σ3，σ1)标在主应力坐标平面，用方程σ1=λσ3进行回归，得到 λ=2.53，进一步计算 φ=25.75°，可以发现预测结果和数值试验结果比较接近(见表8)。

表7 正演计算测试结果Table 7 Test results of forward computation

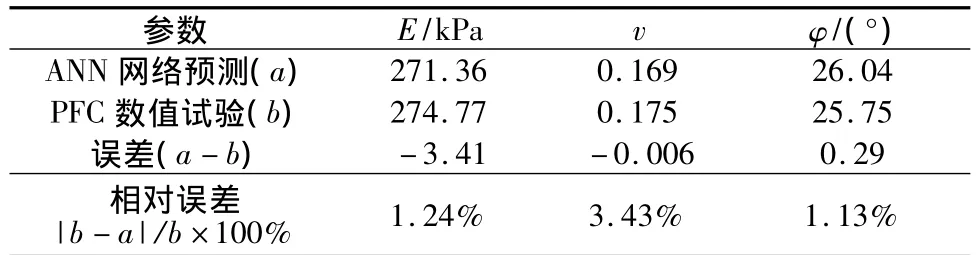
表8 正演计算结果校验Table 8 Verification results of forward computation

5.2 反演计算

建立列向量之间的映射关系:

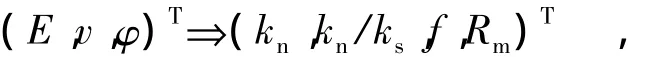
训练形成网络 net2，并测试得出(试样粒度分布3.22～7.22mm)

将细观参数输入PFC双轴试验程序以检验预测结果的正确性，得到表8。同理可得λ=2.54，φ=25.92°，可见预测结果和数值试验结果比较接近，见表9和表10。

表9 反演计算测试结果Table 9 Test results of inversion

表10 反演计算结果校验Table 10 Verification results of inversion

6 结论

本文以无黏结颗粒材料为例，通过一组正交设计的试验，讨论了PFC颗粒细观参数取值对介质宏观特性的影响，并分析了各个细观参量对宏观参量的敏感度，提出了数值实验时宏细观参数匹配调整的基本原则，并利用神经网络实现了宏细观参数间的智能互演，为PFC系列软件在实际岩土工程计算中提供了参考。黏结颗粒材料例如黏土、岩石、混凝土等亦可按照本文的研究思路进行分析。但是本文在分析试样破坏大小应力关系时，采用了摩尔库仑强度理论，认为二者为线性关系，实际上随着侧压的提高，主应力并未严格地按线性比例增大，而是呈现非线性变化，σ3－σ1关系曲线出现逐渐平缓的趋势(这与莫尔理论极为相似)，故可以考虑引入其他的宏观本构模型并研究细观参量对本构参数的影响。

［1］CUNDALL P A，STACK O D L.A Discrete Numerical Model for Granular Assemblies［J］.Geotechique，1979，29(1):47－65.

［2］朱焕春.PFC及其在矿山崩落开采研究中的应用［J］.岩石力学与工程学报，2006，25(9):1927－1931.(ZHU Huan-chun.PFC and Application Case of Caving Study［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(9):1927－1931.(in Chinese))

［3］Itasca Consulting Group，Inc.，PFC2D(Particle Flow Code in 2 Dimensions)，Version1.1［K］.Minneapolis，MN:ICG，1999.

［4］Itasca Consulting Group，PFC3D(Particle Flow Code in 3 Dimensions)，Version1.1［K］.Minneapolis，MN:ICG，1999.

［5］UTILI S，NOVA R.DEM Analysis of Bonded Granular Geomaterials［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2008，32(17):1997－2031.

［6］WANG C，TANANT D D，LILLY PA.Numerical Analysis of the Stability of Heavily Jointed Rock Slopes Using PFC2D［J］.International Journal of Rock Mechanics＆Mining Sciences，2003，40(3):415－424.

［7］GENG Y，YU H S，GLENN M.Simulation of Granular Material Behaviour Using DEM［J］.Procedia Earth and Planetary Science，2009，1(1):598－605.

［8］周 健，王家全，曾 远，等.颗粒流强度折减法和重力增加法的边坡安全系数研究［J］.岩土力学，2009，30(6):1549－1554.(ZHOU Jian，WANG Jia-quan，ZENG Yuan，et al.Slope Safety Factor by Methods of Particle Flow Code Strength Reduction and Gravity Increase［J］.Chinese Journal of Rock and Soil Mechanics，2009，30(6):1549－1554.(in Chinese))

［9］WANG C B，ZHU H H.Study on the Relationship Between Particle Micro-parameters and Soil Mechanical Properties［C］∥ Proceedings of the 1st International Conference on Information Technology in Geo-Engineering(ICITG).Shanghai，China，Sep.16－17，2010:599－606.

［10］李耀旭.颗粒流方法在土石混合体力学特性研究中的应用［D］.武汉:长江科学院，2009.(LI Yao-xu.The Application of Particle Flow Code in Studying of Mechanical Characteristics of Soil-Rock Mixture［D］.Wuhan:Yangtze River Scientific Research Institute，2009.(in Chinese))

［11］王 新.土石混合体力学特性影响因素及破环机制研究［D］.武汉:长江科学院，2010.(WANG Xin.Research on Influence Factors of Mechanics Characteristics and Failure Mechanism of Soil-Rock Mixture［D］.Wuhan:Yangtze River Scientific Research Institute，2010.(in Chinese))

［12］吴贵生.试验设计与数据处理［M］.北京:冶金工业出版社，1997.(WU Gui-sheng.Test Design and Data Processing［M］.Beijing:Metallurgy Industry Press，1997.(in Chinese))

［13］张德丰.Matlab神经网络仿真与应用［M］.北京:电子工业出版社，2009.(ZHANG De-feng.Simulation and Application of Neural Network Based on Matlab［M］.Beijing:Publishing House of Electronics Industry，2009.(in Chinese))