垂直螺旋管道内单颗粒运动受旋转科氏力影响的试验研究
张志雁,牧振伟,杨力行
(1.新疆农业大学水利与土木工程学院,乌鲁木齐 830052;2.新疆水利水电勘测设计研究院,乌鲁木齐 830000)
当研究对象相对于动参考系发生运动时,则该研究对象受到科氏惯性力(简称科氏力)作用。该力的数学表达式为

科氏力可以分为地转科氏力和旋转科氏力。地转科氏力对大尺度的河流、湖泊、海湾等水域水流的影响已是公认的事实[1-4],在小尺度旋转流体运动过程中地转科氏力一般忽略不计[5]。而关于小尺度低速度旋转流如天然含沙水流弯道或人工弯道、排沙漏斗中颗粒所受旋转科氏力的研究尚不多见[6-9]。
本文采用高速摄影方法,拍摄记录并研究垂直矩形螺旋管道内球形单颗粒运动形态,采用单颗粒动力学模型,以探求颗粒在旋转水流中受旋转科氏力的特性。
1 试验装置与材料
1.1 试验装置
试验模型装置(见图1)的进流量可由进口阀门和出口阀门协调控制。模型装置有溢流和回流,整个试验装置为具有恒定水头的自循环系统。试验单颗粒从颗粒导入管进入螺旋管道。

图1 试验模型装置Fig.1 Equipment for the test
矩形螺旋管道模型的几何参数为:有机玻璃管道截面尺寸为30mm×17mm矩形;螺旋管道由长210mm垂直进口段,管轴半径为R=185mm的1/4圆,及管轴半径分别为R=165mm,125mm,85mm和R=145mm,105mm,65mm等不同半径的半圆结构组成。
1.2 试验材料
试验颗粒选用塑料小圆球,粒径dP=5.85mm,密度ρp=1.235 g/cm3。所用的仪器有电子天平、高速摄像机等。
2 试验方法与工况
试验采用称重法量测水流流量。采用高速照相机捕获单颗粒运动轨迹。通过高速摄影技术对颗粒的运动轨迹进行拍摄,选取满足条件的一系列图像,从光学成像理论出发,采用Matab软件对记录图像的可辨性及失真程度进行分析[10];通过对单颗粒在旋转水流中的运动距离、运动方位及运动时间等参数的测量,计算获得单颗粒的速度、角速度等参数。以单颗粒所在管道半径的圆心作为基准点,计算并确定单颗粒中心的坐标位置。
根据单颗粒在垂直矩形螺旋管道内发生运动作为来流条件,共进行了5组试验,试验流量Q分别为149.550,153.900,199.213,215.119,285.742cm3/s。
3 试验结果与分析
颗粒受力分析是固液两相流中固体颗粒运动研究的核心问题。在实际应用中,许多多相流是由宏观上连续的气体或液体相与离散的颗粒相组成的。研究这类多相流最简单的方法,就是采用单颗粒动力学模型[11]。该模型不考虑由颗粒的存在造成的对连续相流体流动的影响,也不考虑颗粒之间的相互作用以及颗粒的脉动,并认为连续相的流场已知,只考虑颗粒在连续相流体中的受力和运动。这是一种单向耦合模型,得到较广泛的应用[12-13]。
单颗粒在螺旋管道中的运动非常复杂,在单颗粒动力学模型中,若在拉格朗日坐标系中考虑固相颗粒运动时,单颗粒运动方程可直接从牛顿第二定律得出,即

式中:mp为固体颗粒的质量;up为固相颗粒的速度矢量;∑Fi包括固相颗粒所受的有效重力FEF、阻力FR、离心力FCE、旋转科氏力FCO、虚假质量力FVM、压力梯度力、Basset力、Maguns力、Saffman 力等各力,各力计算方法可以参考文献[8](不考虑颗粒在水流中的自转作用,压力梯度力、Basset力、Magnus升力和Saffman升力等可以忽略不计[11])。

图2 颗粒受力大小随时间的变化Fig.2 Changes of forces upon particle with time
为便于理论分析,选取单颗粒运动轨迹较理想(即颗粒与边壁在运动中不发生碰撞)的工况进行研究,规定速度、力等矢量变量背离圆心为正方向及顺水流方向为正方向。
在各试验工况,球形单颗粒在垂直矩形螺旋管道内右侧作上升运动,在左侧作下降运动,最后顺着水流流出管道。为研究不同流量、不同管轴半径内单颗粒所受各种力随时间变化的关系,选取Q=149.550cm3/s和Q=215.119cm3/s 2 组流量进行分析,见图2。
由图2可见:
(1)单颗粒在不同流量不同的管轴半径下作上升和下降运动过程中,主要受到离心力、有效重力、旋转科氏力及阻力的作用,而颗粒所受的虚假质量力的作用很小。
(2)在不同流量下随连续相水流运动过程中,单颗粒所受到的旋转科氏力与阻力在数量级上相同,并且两者的大小基本同步增大或减小。一般情况下,颗粒受到的旋转科氏力比阻力大。
(3)颗粒所受离心力、旋转科氏力及阻力随流量的增大而增大。在上升过程中,颗粒受到的旋转科氏力与离心力随时间的变化较小,而在下降过程中,颗粒受到的旋转科氏力与离心力随时间的变化较大些,说明在下降过程中,颗粒的速度变化较大,同时颗粒与连续相水流的法向相对速度也较大,而在上升过程中则相反。
为了研究速度无量纲量λ=Vp.tan/Vf=Vp/Vf与力的无量纲量ζ=FCO/FCE的关系,把所有6组试验工况的数据共计468个样本点绘在一起,ζ的指数拟合曲线见图3。

图3 λ与ζ的关系Fig.3 Relation between λ and ζ
通过回归分析,获得两者的关系,可用方程表示为
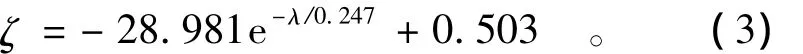
方程的相关系数为0.995,说明λ与ζ存在明显的指数关系。由图可见,随着无量纲量λ的增大,ζ也逐渐增大。当λ=1时,颗粒速度相对水流速度为零,此时,颗粒所受旋转科氏力为零;当λ>1时,颗粒速度相对水流速度大于零,则颗粒所受旋转科氏力与离心力的方向相同,均为背离圆心方向,随着λ的增大,ζ增大的幅度有所减小;当λ<1时,颗粒速度相对水流速度小于零,则颗粒所受旋转科氏力与离心力的方向相反,随着λ的减小,ζ减小的幅度有所增大。
假设当颗粒受到的旋转科氏力小于离心力一个数量级时,可以认为旋转科氏力忽略不计。表1为不同试验工况下所有样本点ζ大小的分布情况,从表中可以看出,ζ<-1.0的样本仅有14个,说明颗粒受到的旋转科氏力大于离心力的情况极少。颗粒所受旋转科氏力不能忽略并且与离心力的方向相反(即ζ<-0.1)的样本数也只有167个,不足总数的1/3,并且旋转科氏力量值大于离心力量值一半的情况也很少发生。而旋转科氏力与离心力在同一方向时对颗粒的作用很可能被认为是仅有离心力的作用,因此,颗粒受到旋转科氏力时常被忽略。试验证明,颗粒所受旋转科氏力可以忽略(即0.1>ζ>-0.1)出现次数相对较少,约占总样本的1/4,即试验中颗粒所受旋转科氏力与离心力在同一数量级的概率为3/4。因此,在小尺度低速度旋转流下研究颗粒受力时,颗粒所受的旋转科氏力不应被忽略。

表1 试验样本点ζ的分布Table 1 Distributions ofζ
4 结论
采用高速摄影方法拍摄记录垂直矩形管道内单颗粒的运动,捕捉试验中颗粒的运动轨迹,获得其运动参数,并采用单颗粒动力学模型分析颗粒所受力的规律,得到以下主要结论:
(1)颗粒在运动过程中主要受到离心力、有效重力、旋转科氏力及阻力的作用。随着流量的增加或管轴半径的减小,颗粒所受离心力、旋转科氏力及阻力都逐渐增大。
(2)无量纲量λ与ζ存在明显的指数关系。当λ=1时,颗粒所受旋转科氏力为零;当λ>1时,颗粒所受旋转科氏力与离心力的方向相同,均为背离圆心方向;当λ<1时,颗粒所受旋转科氏力与离心力的方向相反。
(3)试验中颗粒所受旋转科氏力与离心力在同一数量级的概率为3/4。因此,在小尺度低速度旋转流中研究颗粒受力时,颗粒所受的旋转科氏力不应被忽略。
以上结论将为排沙漏斗、弯道水流等小尺度旋转流内的泥沙运动研究提供一条新的思路。另外,试验仅对颗粒所受的阻力、有效重力、离心力、旋转科氏力及虚假质量力进行了分析,由压力梯度力、Basset力、Magnus升力等力对颗粒运动的影响作用,尚需进一步探讨。
[1]李国英.黄河河势演变中科氏力的作用[J].水利学报,2007,38(12):1409-1413.(LI Guo-ying.Effect of Coriolis Force on Morphology Evolution of Yellow River[J].Hydraulic Engineering,2007,38(12):1409-1413.(in Chinese))
[2]岳前进,张 希,季顺迎.辽东湾海冰漂移的动力要素分析[J].海洋环境科学,2001,20(4):24-39.(YUE Qian-jin,ZHANG Xi,JI Shun-ying.Dynamic Analysis of Drifting Ice in the Liaodong Bay[J].Marine Environmental Science,2001,20(4):24-39.(in Chinese))
[3]高钰涯.尼亚加拉河流及瀑布演化浅析[J].水资源保护,2008,24(6):80-84.(GAO Yu-ya.Preliminary Research on the Evolution of Niagara River and Niagara Falls[J].Water Resources Protection ,2008,24(6):80-84.(in Chinese))
[4]刘凤岳,武桂秋.科氏力对黄河口淤积延伸和摆动的影响[J].人民黄河,1987,9(4):33-36.(LIU Fengyue,WU Gui-qiu.Coriolis Force on the Sediment Extension and Swing of the Yellow River Mouth[J].Yellow River,1987,9(4):33-36.(in Chinese))
[5]WELLSM G.How Coriolis Forces Can Limit the Spatial Extent of Sediment Deposition of a Large-Scale Turbidity Current[J].Sedimentary Geology,2009,218:1-5.
[6]杨力行,侯 杰,沈晓阳.科氏力与水流涡旋成因初探[C]∥第九届全国泥沙信息网学术研讨会论文集.乌鲁木齐:新疆人民出版社,2000:136-137.(YANG Lixing,HOU Jie,SHEN Xiao-yang.Preliminary Study on the Causes of Vortex Flow and Coriolis Force[C]∥Proceedings of the Ninth Academic Symposium of National Network of Sediment.Urumqi:Xinjiang People Press,2000:136-137.(in Chinese))
[7]沈晓阳.科氏惯性力对曲线型沉沙池排沙效果影响的探讨[C]∥第九届全国泥沙信息网学术研讨会论文集.乌鲁木齐:新疆人民出版社,2000:133-135.(SHEN Xiaoyang.Coriolis Effect on the Curved Sediment Settling Basin[C]∥Proceedings of the Ninth Symposium of National Sediment Information.Urumqi:Xinjiang People Press,2000:133-135.(in Chinese))
[8]张志雁,牧振伟,苏 枋,等.垂直螺旋管道内球形单颗粒受旋转科氏力分析[J].人民黄河,2010,32(11):135-137.(ZHANG Zhi-yan,MU Zhen-wei,SU Fang,et al.Analysis of Rotational Coriolis Force on Spherical Single Particle in Vertical Spiral Duct[J].Yellow River,2010,32(11):135-137.(in Chinese))
[9]汪艺义,苏 枋,胡景龙,等.小尺度旋转两相流中泥沙科氏力的作用[J].人民黄河,2010,32(6):40-41.(WANG Yi-yi,SU Fang,HU Jing-long,et al.Coriolis Effect on Sediment in Small-Scale Rotational Two-phase Flow[J].Yellow River,2010,32(6):40-41.(in Chinese))
[10]薛 瑞,邵建斌,陈 刚,等.基于MATLAB的泄洪洞气泡运动轨迹检测[J].水利与建筑工程学报,2008,6(2):22-24.(XUE Rui,SHAO Jian-bin,CHEN Gang,et al.Detection for Motion Tracks of Bubbles in Spillway Tunnel Based on Matlab[J].Journal of Water Resources and Architectural Engineering,2008,6(2):22-24.(in Chinese))
[11]车得福,李会雄.多相流及其应用[M].西安:西安交通大学出版社,2007.(CHE De-fu,LI Hui-xiong.Multiphase Flow and Its Application[M].Xi’an:Xi’an Jiaotong University Press,2007.(in Chinese))
[12]ZHOU L X,LIN W Y,JIANG Z.Numerical Modeling of Evaporating Spray Two-phase Flows Caused by Opposite Injection of a Swirl Atomizer in Duct[J].Combustion Science& Technology,1984,3:56-64.
[13]李会雄,栾合飞,陈听宽,等.注水井投球调剖工艺的理论与实验研究[J].油田化学,2003,20(2):113-118.(LI Hui-xiong,LUAN He-fei,CHEN Ting-kuan,et al.Theoretical and Experimental Studies on Water Injectivity Profile Modification by Using Rigid Plastic as Perforation Closer[J].Oilfield Chemistry,2003,20(2):113-118.(in Chinese))

